海洋资源四维勘探拖缆阵列动力学特性仿真研究

吴喆莹，张维竞，刘 涛，张广磊，史斌杰

(上海交通大学海洋工程国家重点实验室，上海 200240)

海洋资源四维勘探拖缆阵列动力学特性仿真研究

吴喆莹，张维竞，刘 涛，张广磊，史斌杰

(上海交通大学海洋工程国家重点实验室，上海 200240)

面对日益增长的海洋资源勘探需求，海洋资源四维勘探拖缆阵列的研究越来越被人们所重视。作为拖缆动态控制策略研究的前提与依据，拖缆阵列的动力学特性始终是该领域在技术突破进程中的重要课题。以Ablow的经典模型为基础，采用微元法对拖缆阵列建立三维模型，并在时域上采用广义α算法对非线性方程进行离散求解，通过程序编译，对拖缆在四种工况(即拖船匀速直线航行、回转航行、变速直线航行以及拖点处存在升沉运动等)下的响应进行计算分析，着重考量其深度及张力的变化。仿真计算结果表明，广义α算法对拖缆阵列姿态在空间和时间上离散求解，算法稳定性良好，弥补了传统有限差分法对于时域不稳定的缺陷。

海洋勘探;拖缆阵列;广义α算法;动力学特性;仿真

海洋中蕴藏着丰富、巨量的油气资源［1］，海洋资源的勘探与开发已成为能源发展的重点和热点。海洋资源四维勘探是目前海底探查成效最高的地球物理技术，它建立在海洋声学的基础上，依靠水下拖曳系统来实现勘探作业［2］。水下拖曳系统通常由水面拖曳母船、拖缆、尾绳及各拖曳设备等组成一个复杂系统，掌握其在各种情况下动力学特性，特别是水下拖缆的动力学特性，对系统工作效率提升、系统稳定性保障等有着重要作用。

目前国内外拖缆系统的动力学模型较为成熟，主流的有 Ablow 和 Schechter［3］，Sanders［4］，Delmer［5］，Mili-nazzo［6］等提出的三维模型。其中，Ablow和Schechter以及Milinazzo采用有限差分法来求解模型;Delmer采用有限元法求解问题。近年来也有不少研究者用集中质量法、有限差分法、直接积分法等求解拖缆系统的动、稳态运动［7-12］。基于前人的研究与探索，采用Ablow和Schechter的经典模型，采用广义α算法求解三维拖缆方程，并对典型工况(包括匀速直线航行、回转航行、变速直线航行、船体升沉运动等工况)下的拖缆动力学特性进行仿真研究，为后期控制策略的深入研究做好铺垫。

1 拖缆动力学模型

依据Ablow与Schechter提出并经实验有效验证的模型，假设拖缆为圆柱型柔性缆，忽略拖缆弯曲应力［13］和海流的影响，有如下方程:

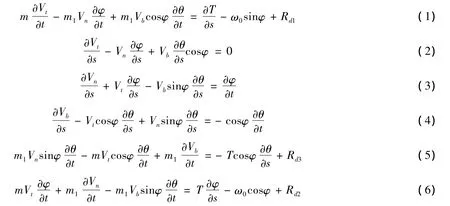
图1 欧拉角(θ，ψ，φ)示意(ψ =90°)Fig.1 Illustration of(θ，ψ，φ)(ψ =90°)

定义 Y(s，t)=(T，Vt，Vn，Vb，φ，θ)T，则上述方程(1)～ (6)有矩阵形式:

其中，

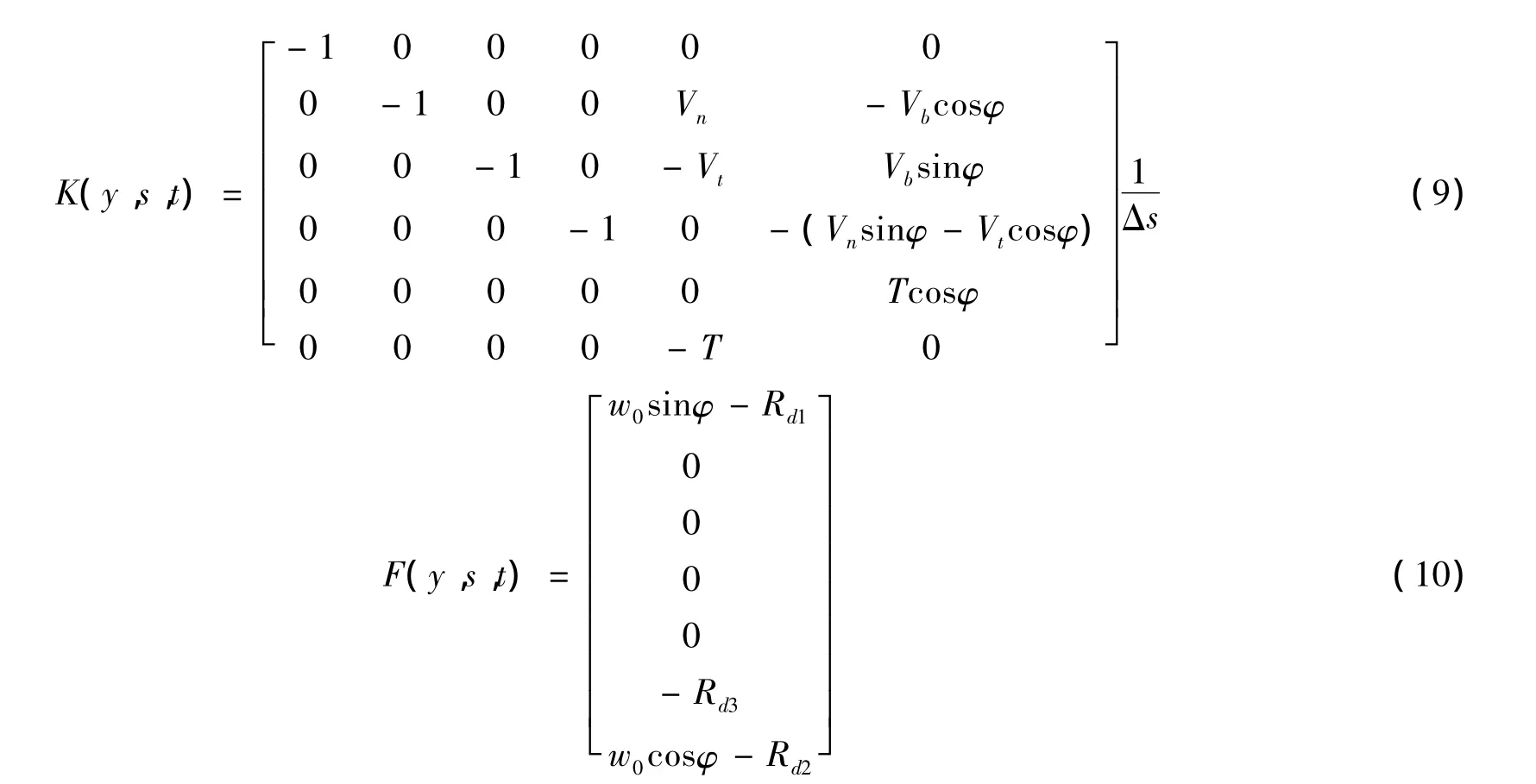
2 边界条件

2.1 拖缆首端边界条件

首端缆上拖点的速度与拖船速度相同，即

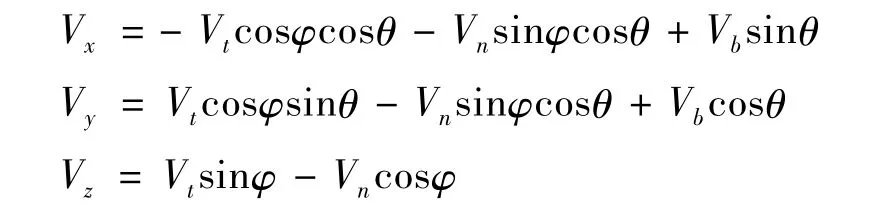
式中:Vx，Vy，Vz为拖船航速在固定坐标系 x，y，z方向上的分量。

2.2 尾端边界条件

文献［12］、［14］等中对于拖缆系统尾端边界条件设为自由端并定义张力T=0。实际工况中，拖缆系统尾端有尾浮，其一般在拖缆末端产生一个较大的预张力以增加系统的稳定性及可控性。由于尾浮与拖缆间的耦合作用，拖缆的运动将变得非常复杂，而尾浮在侧向的偏移很小，其侧向与纵向的耦合可以忽略，仅在速度方向上取近似阻力［15］。

参考Egil Pedersen［16］的实船试验，在稳态情况下简化假设尾浮对拖缆系统提供一个定常的张力T=T0。

3 拖缆方程的离散

3.1 空间离散

拖缆方程在空间上的离散参考Ablow和Schechter采用的基于二阶精度的有限差分方法，假设将拖缆划分为n个节点，记j为第j个空间点(j=1，2，…，n)，则拖缆的动态方程可离散为n－1个矩阵方程:

3.2 时间离散

然而，有限差分方法在时间离散求解上并不稳定［17］。对此，Gobat曾将广义α算法用于二维拖缆方程的求解中，并已获得良好的精度和稳定性［17-18］。经验算，将广义α算法用到了三维拖缆方程的求解中，对方程在时间上进行离散。

广义α算法在时间上的离散形式:

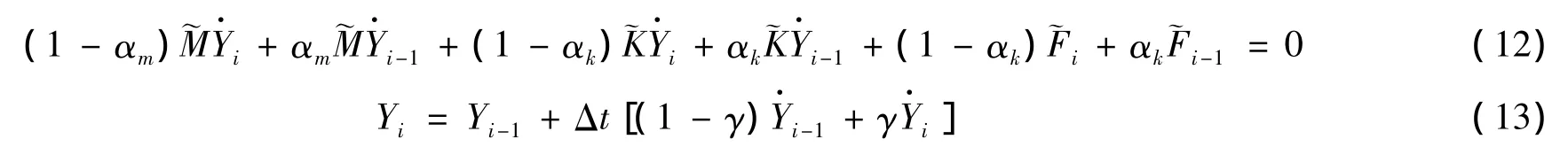
式中:Δt表示时间步长，αm、αk和γ则构成了广义α算法，i为第i个时间点。

由于广义α算法在求解线性问题时，系数矩阵M、K恒定不变，因此可以用式(12)进行计算。但是对于非线性问题系数矩阵会随时间的变化而改变，算法的稳定性将随时间有条件收敛。为避免该问题以提高算法的稳定性，采用系数矩阵与速度矢量、位移矢量具有相同权重的方法。此时，算法的表达形式变为

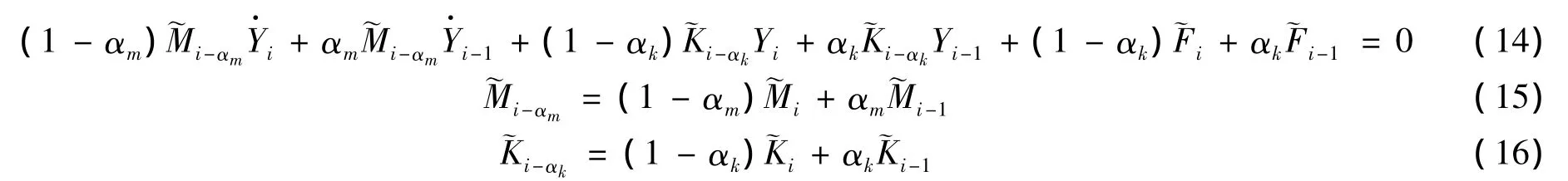
4 典型工况仿真计算结果

在前期的研究中，通过与Ablow在1983年所做实验的数据进行对比验算，并结合近期在拖曳水池所做的模型试验的趋势分析结果，表明利用广义α算法求解拖缆动力学模型是可靠的［19］。在此基础上，进行进一步动力学特性仿真分析。

4.1 拖缆系统稳态仿真

4.1.1 考虑尾拖作用的拖缆系统稳态仿真

1)仿真参数

在当前的实际勘探作业中，阵列缆的长度一般为3 000～8 000 m长，勘探船一般以4～5节的船速航行。参考文献［11］、［15］、［16］等中的拖缆参数，这里以250 m长的引导拖缆、3 000 m长阵列缆和50 m长的尾缆作为研究对象。

以10 m为一段，将引导拖缆分为25段，阵列缆分为300段，尾缆分为5段，共330个分段;以尾端为初始点(第1点)标记，直至拖缆与拖船结合点(即拖点)为末位点第331点，总共331个节点。其中，阵列缆在水中的净浮力为零(拖缆参数见表1)。

表1 拖缆系统的物理特性Tab.1 Physical properties of the towed cable

拖曳船以一定速度拖带拖缆系统沿直线稳定航行，拖曳系统尾部考虑拖船作用时，将其近似为尾部张力T=T0。参考并引用Egil Pedersen［16］实验结果，在拖船速度为 2.0 m/s 和2.6 m/s时分别取尾端水阻力(Fd)为406 N和743 N，则拖缆尾端边界条件如表2所示。

2)仿真计算结果

分别计算该条件下拖船以2.0 m/s和2.6 m/s速度沿直线稳定航行工况下，仿真结果如图2和图3。

表2 拖缆尾端边界条件Tab.2 Boundary conditions at the end of towed cable

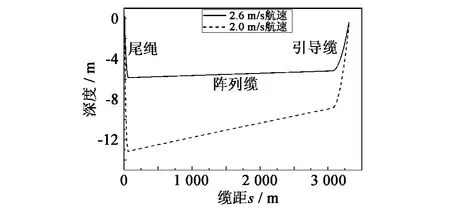
图2 考虑尾拖船时拖缆在匀速直线拖曳工况下深度响应Fig.2 Position of towed cable with tail boat in steady straight course

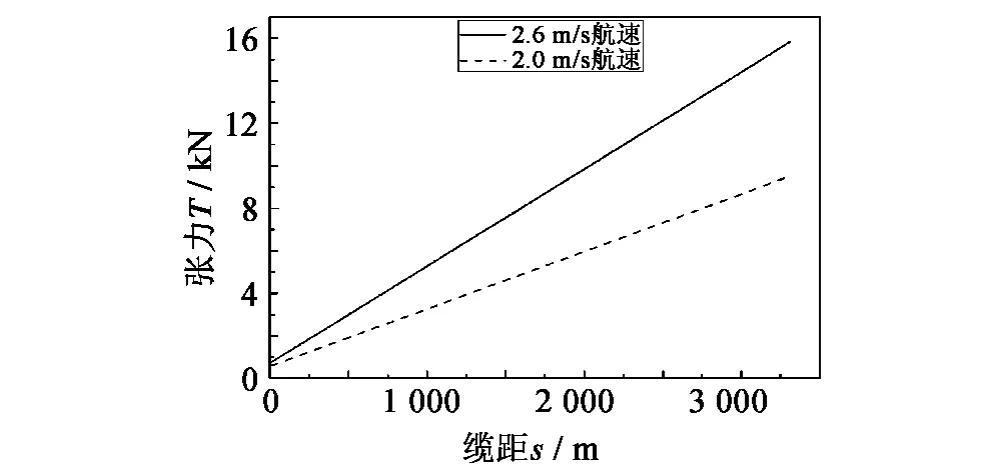
图3 考虑尾拖船时拖缆匀速直线拖曳工况下张力响应Fig.3 Tension of towed cable with tail boat in steady straight course

结果显示:2.0 m/s拖曳速度下，由于引导缆与尾绳净浮力不为零且拖船速度较慢，阵列缆深度在－8.8～－13 m之间，当拖船速度增大时，拖缆阵列有所上浮且整条缆姿态更趋于平稳(见图2)，同时全缆各处的张力均匀变化，在即定速度拖带下，拖缆拖点处所承受的张力最大，尾端张力最小(见图3)。

4.1.2 不考虑尾拖作用的拖缆系统稳态仿真

1)仿真参数

［12］、［14］、［15］中，当不考虑尾浮时，尾端可近似看做自由端，且有T=0。由于此时拖缆尾端为自由端，为了使尾绳在水中的重力影响拖缆原有的姿态，将尾绳调整水中净浮力为零的缆，参数详见表3。

表3 拖缆系统的物理特性Tab.3 Physical properties of the towed cable

2)仿真结果

结果显示:2.0 m/s拖曳速度下，阵列缆深度维持在－8.8 m左右;2.6 m/s拖曳速度下，阵列缆深度维持在－5.4 m左右(图4)。由于阵列缆为零浮力缆，其在水中姿态平稳。全缆各处的张力变化趋势不变(对比图5与图3)。

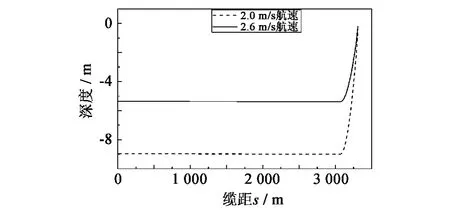
图4 不考虑尾拖船时匀速直线拖曳工况下拖缆深度图Fig.4 Position of towed cable without tail boat in steady straight course

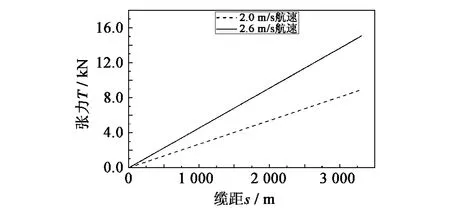
图5 不考虑尾拖船时拖缆匀速直线拖曳工况下张力响应Fig.5 Tension of towed cable without tail boat in steady straight course

4.2 拖缆系统动态仿真

拖缆分段方式及节点选取方式同稳态情况下的仿真计算一样，拖缆参数详见表3，各工况下的仿真不计尾拖船的影响。

4.2.1 拖船回转航行

船舶以一定速度拖带系统回转。计算工况:初始时刻，拖船系统以vx=2 m/s的速度匀速稳定直航;此后，进入半径为1 000 m的回转运动并完成180°回转;最后，仍以vx=2 m/s的速度开出，并持续航行至稳定状态。仿真6 000 s后，结果如图6和图7所示。

图6 回转航行缆上各点深度随时间变化曲线Fig.6 Response of depth on different points of towed cable under circular manoeuver

结果显示:拖缆上的点在进入回转状态时先有所下沉，在回转运动的尾声接近最低点，之后再缓慢上浮并趋近初始平衡位置(如图6所示);对比图6(a)与图6(b)，缆上后端位置的点在回转过程中深度的波动幅度小于缆上前端位置的点;拖点处张力在此过程中，先缓慢变小并于回转运动的尾声到达最低点，之后张力缓慢增加并趋近初始平衡位置水平(如图7)。这与文献［15］所得的结果趋势相符。

4.2.2 拖船沿直线变速航行

船舶开始以vx=2.6 m/s的的速度沿直线行驶，假定某一时刻沿航行方向(即vx方向)船速做幅值为0.1 m/s，周期为1 000 s的正弦变化来模拟实船直线变速航行工况。仿真3 000 s后得结果如图8和图9所示。

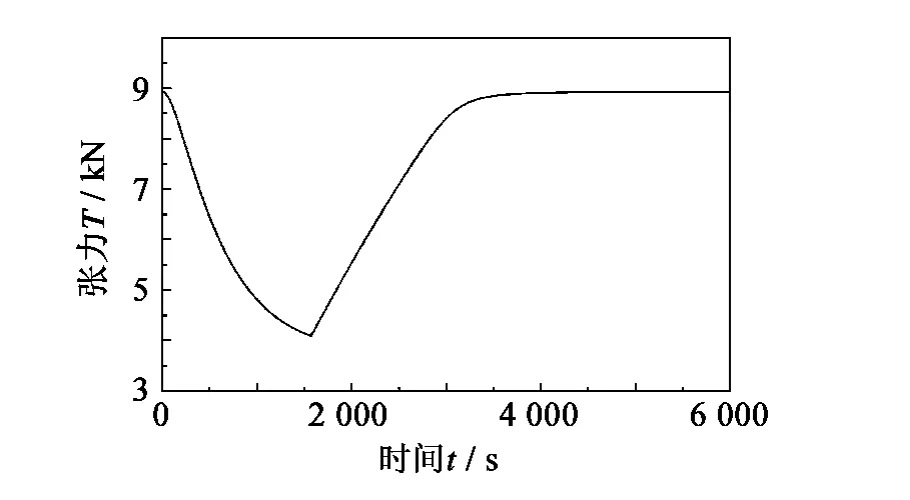
图7 回转航行拖点处张力随时间变化曲线Fig.7 Response of tension at towed point of the towed cable under circular manoeuver

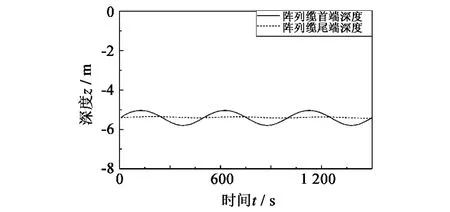
图8 直线变速航行拖缆各位置深度沿时间变化Fig.8 Response of depth at certain points of towed cable during speed change of straight run

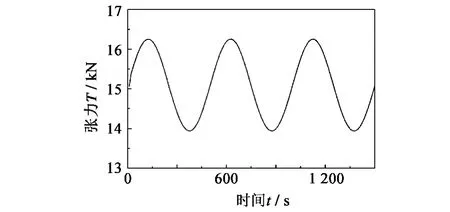
图9 直线变速航行拖点张力沿时间变化Fig.9 Response of tension at towed point of towed cable during speed change of straight run

结果显示:1)在船舶变速直线行驶过程中，缆上各点的深度波动变化不大，较之缆长可以忽略不计;2)对于低频扰动，拖缆深度变化的影响难以传到尾端，故尾端在深度上基本没有变化;3)拖缆上各点张力变化却非常大，在±0.1 m/s速度变化的情况下拖点处张力变化范围超过2 kN。

4.2.3 拖点处有升沉运动

船舶以vx=2.6 m/s的速度沿直线航行，在拖点处沿深度方向(即vz方向)增加正弦变化速度以模拟拖点处升沉运动，其幅值为1.59 m，周期为10 s。仿真结果如图10和图11。

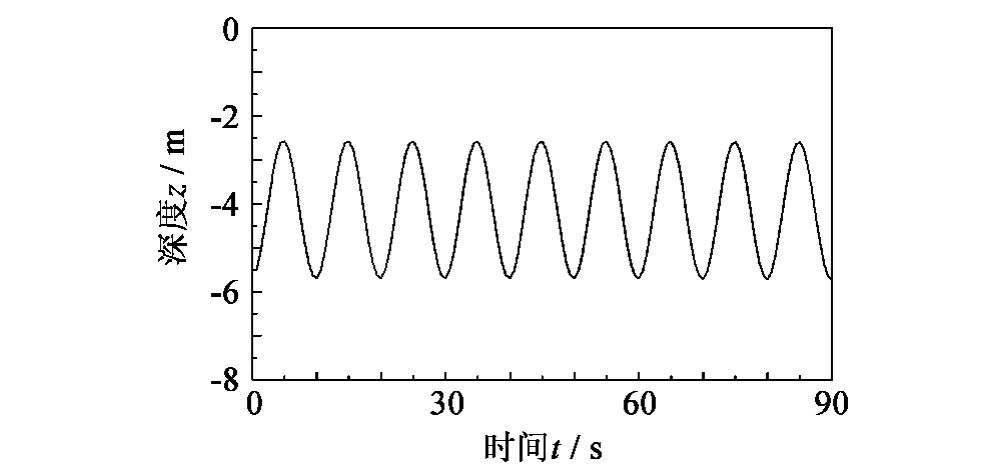
图10 升沉运动时阵列缆首端深度变化Fig.10 Response of depth at certain points of towed cablein heaving motion

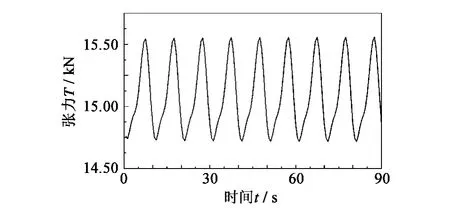
图11 升沉运动时拖点张力变化Fig.11 Response of tension at certain pointss of towed cable in heaving motion

结果显示:拖缆在深沉运动激励下深度变化较为明显;然而张力变化相对直线变速工况而言变化较小。

通过上述计算，可以看出在时间步长从0.625 s到10 s，仿真时间从100 s到6 000 s过程，工况从直线稳定到回转运动、变速直线运动以及拖点升沉运动的状况下都未出现不稳定情况。再次表明，这里所用广义α算法稳定性良好，进一步验证了此算法在求解拖缆动力学模型是正确可行的。仿真结果可为下一步制定拖缆在上述工况下的动态控制策略给出了良好的分析依据。

5 结语

采用微元法对海洋资源四维勘探拖缆阵列建立三维动力学模型进行动力学特性研究，并用广义α算法对拖缆阵列姿态在空间和时间上离散求解，弥补了传统有限差分法对于时域不稳定的缺陷。通过计算机仿真程序编译，算出拖缆在匀速直线航行、回转航行、变速直线航行以及拖点升沉运动四种工况下拖缆的动力学特性，为后续进一步探究拖缆动态控制策略及缆上控制器设计等提供了依据。

参考文献:

［1］赵政璋，赵贤正，李景明，等.国外海洋深水油气勘探发展趋势及启示［J］.中国石油勘探，2005(6):71-76.

［2］陈小宏，牟永光.四维地震油藏监测技术及其应用［J］.石油地球物理勘探，1998(6):707-715.

［3］Ablow C M，Schechter.Numerical simulation of undersea cable dynamics［J］.Ocean Engineering，1983(10):443-457.

［4］Sanders J V.A three-dimensional dynamic analysis of a towed system［J］.Ocean Engineering，1982，9(5):483-499.

［5］Delmer T N，Stephens T C，Coe J M.Numerical simulation of towed cables［J］.Ocean Engineering，1983，10(2):119-132.

［6］Milinazzo F，Wilkie M，Latchman S A.An efficient algorithm for simulating the dynamics of towed cable systems［J］.Ocean Engineering，1987，14(6):513-526.

［7］Wang F，Huang G L，Deng D H.Steady state analysis of towed marine cable［J］.Journal of Shanghai Jiao Tong University:Science，2008，13(2):239-244.

［8］Sun Y，Leonard J W，Chiou R B.Simulation of unsteady oceanic cable deployment by direct integration with suppression［J］.O-cean Engineering，1994，21(3):243-256.

［9］Huang S.Dynamic analysis of 3-dimensional marine cables［J］.Ocean Engineering，1994，21(6):587-605.

［10］张维竞，张小卿，陈 峻.基于嵌入式水鸟的海洋地震拖缆运动状态仿真研究［J］.海洋工程，2009，27(4):81-86

［11］王春杰，张维竞，刘 涛，等.横向海流作用下海洋地震拖缆姿态控制［J］.大连海事大学学报，2011，37(1):9-17.

［12］邓德衡，黄国樑，楼连根.拖曳线列阵阵形与姿态数值计算［J］.海洋工程，1999，17(1):17-26.

［13］王 飞，陈锦标，涂兴华.低速低应力时拖缆运动仿真［J］.上海交通大学学报，2010，44(6):828-832.

［14］罗 薇，张 攀.拖缆系统运动仿真［J］.武汉理工大学学报，2005，29(5):724-726

［15］王 飞.海洋勘探拖曳系统运动仿真与控制技术研究［D］.上海:上海交通大学，2006.

［16］Egil Pedersen.A Nautical Study of Towed Marine Seismic Streamer Cable Configurations［D］.Doctoral Thesis in Nautical Engineering of Norweigian University of Science and Technology，1996.

［17］Jason I Gobat.The Dynamics of Geometrically Compliant Mooring Systems［D］.Massachusetts Institute of Technology，Woods Hole Oceanographic Institution，2000.

［18］Gobat J I，Grosenbaugh M A.Time-domain numerical simulation of ocean cable structures［J］.Ocean Engineering，2005(33):1373-1400.

［19］张广磊，张维竞，刘 涛.广义α算法在拖曳阵列动态仿真中的应用研究［J］.哈尔滨工程大学学报，2012，33(5):1-6.

Simulation study on dynamic characteristics of towed array for four-dimensional exploration of marine resources

WU Zhe-ying，ZHANG Wei-jing，LIU Tao，ZHANG Guang-lei，SHI Bin-jie
(National Key Laboratory of Ocean Engineering，Shanghai Jiao Tong University，Shanghai 200240，China)

In the face of the growing demand of marine resources exploration，studies are increasingly concentrated on towed array for four-dimensional exploration of marine resources.As the premise and basis of further study on dynamic control strategy of towed array，dynamic characteristics of towed array are always the crucial task of technology development in this field.Based on the classic Ablow model，a three-dimensional model is established by applying micro-element method to towed array in this paper and a generalized-α algorithm is introduced to temporally discrete and solve the nonlinear equations.By programming，the computation analysis of response of towed cable，especially the variation in depth and tension，under four different motions，such as steady straight motion，circular manoeuver motion，speed changing motion and heaving motion，is made，which provide an important basis for the following research in making dynamic control strategy of towed array.

marine resources exploration;towed cable;generalized-α;dynamic characteristics;simulation

P741

A

1005-9865(2012)04-0118-07

2011-11-18

国家自然科学基金资助项目(51079083)

吴喆莹(1986－)，女，上海人，硕士生，主要从事轮机工程方向的研究。E-mail:tracywzy@sjtu.edu.cn

张维竞。E-mail:wjzhang@sjtu.edu.cn