斜坡面波浪冲击力试验研究及现场资料分析

冯卫兵，张 惠，郝青玲

(1.河海大学港口海岸及近海工程学院，江苏 南京 210098;2.南海舰队 湛江设计所，广东 湛江524003)

斜坡面波浪冲击力试验研究及现场资料分析

冯卫兵1，张 惠1，郝青玲2

(1.河海大学港口海岸及近海工程学院，江苏 南京 210098;2.南海舰队 湛江设计所，广东 湛江524003)

通过莆田试验站实测资料分析和物理模型试验，对单一斜坡护面板的打击力进行了研究，阐述了斜坡上最大相对波压力和波坦、堤坡坡度以及水深的关系，提出了波压力、波压力打击点位置以及波压力沿斜坡分布的计算公式，并给出了不同累积频率下的波压力换算关系。

不规则波;斜坡堤;波浪打击力;波压力;莆田

斜坡式防浪结构以其造型简单，对地基要求低，施工方便，消波性能好等优点被长期、广泛使用。其护面常采用抛石、干砌块石、人工块体等。在波浪较大地方，护面层采用人工块体防护，在波浪不大的地方，如土坝、水库库岸、运河护坡等，特别是在石料缺乏的地区，常常采用混凝土和钢筋混凝土板作护坡。

在波动过程中由于面板受到向下、向上两个方向波压的反复作用，面板可能出现不同形式的破环。一种情况是面板在浮托力作用下，由于自重不足引起的整体失稳，表现为面板绕上缘或绕下缘的转动，造成面板移位，沿接缝处上翘，整板向上浮动等等，这是较多发生在面板尺寸不大，板厚不足的情况。另一种破坏形式面板发生裂缝、断裂，它由多种原因引起，如面板强度不够，在波浪冲击力打击下产生裂缝、断裂;或由于垫层移动、土体沉陷等原因引起的面板支撑条件恶化导致面板破坏［1］。

混凝土板护坡的设计计算内容是根据其工作特性而决定的。目前多数情况下混凝土板的设计只进行浮托力作用下的整体稳定性验算以及波浪冲击压力作用下的强度计算。一般计算程序为先按整体稳定性要求确定所需的混凝土板厚度，在此基础上再进行强度计算。混凝土板护面强度计算首先应确定作用于其上的波浪产生的波动压力。

关于波浪对斜坡面打击力的计算在国内应用最为广泛的是前苏联规范采用的波压力公式，该方法从规则波在斜坡上破碎后水质点运动方程出发基于射流理论并引入一些系数半理论半经验地导得斜坡坡面上波压力公式［2］。该公式在20世纪70、80年代又利用大型波浪水槽试验加以完善。近年来国内有关单位对斜坡堤压力进行了一些研究，王鉴义［3］等通过对前苏联规范方法进行试验验证，得到前苏联规范公式应用于不规则波计算时，只需将计算式和图表中的规则波波高换成不规则波的有效波高;计算其他累积频率的压力，将求得的有效压力乘以文中给定的换算系数即可。钟南艳［4］对不规则波的冲击力也进行较系统试验。此外，规则波对斜坡打击力的计算还有 ШАНКИН 方法、Fuhboter A 方法［5］、S Neelamani方法［6］，钟瑚穗方法［7］等等。不规则波有夏依坦(ШАЙТАН)基于水库观测资料整理提出的方法，但该方法未考虑坡度的影响，应用上受到一定限制。

利用莆田试验站现场测得的一些波压力资料的整理分析，同时在室内进行不同堤坡坡度，不同波坦，不同相对水深条件下的不规则波压力试验，并提出波浪打击力计算方法。

1 莆田海堤试验站现场观测资料分析

1.1 莆田站简况

莆田海堤试验站位于福建省兴化湾内南洋海堤镇海堤段，水深不大，最大堤前水深2.4 m左右，该地常年受台风影响，大风速均为台风引起，观测到最大风速25.4 m/s，实测最大波高为1.3 m。试验堤段全长185 m，设4个观测断面，全部为干砌规整花岗岩护面，波压力观测在m=3的单坡断面上进行。在断面中部开一0.3 m宽的槽子，可安放平面尺寸0.3 m×0.3 m的混凝土块。在混凝土块中部放置外直径为10 cm的电阻式传感器，传感器中心部为直径6 cm的波纹圆形钢片，自振频率为400 Hz左右。压力传感器沿斜坡布置为4～5个，堤脚水平底处1个。斜坡上传感器间距为0.6～1.2 m不等。波压力现场资料为1965年7～9月中6次受台风影响时观测得到的。波要素观测通过在堤前80 m设置的电接触式波高仪和堤前20 m处测波杆(目测)进行观测。波压力和波要素记录采用16线紫外线示波器。

1.2 资料整理方法

采用波压力观测记录中比较完整的14组资料，每组记录波数大约为200个左右。波压分析时统计求出各测点压力峰平均值¯p，有效值p1/3，十分之一大值平均值p1/10，及该组的最大压力峰值pmax。由于一般情况下有效值较为稳定，故采用有效值分析其变化规律。对应波要素采用有效波高HS及平均波周期¯T，最后求出各组次各测点的相对波压力ps/γHS。

1.3 波压力沿斜坡分布

根据整理出来的数据，作出相对波压力沿斜坡分布规律图，但由于台风影响期间现场观测条件较差以及当时仪器设备条件的限制，常出现个别传感器失效的情况，使一些组次记录的波压力沿斜坡分布的资料不完整。图1为1组波压分布的示例，图2为所有组次汇总。由图1、2可见，波浪在水下一定距离的打击点附近出现ps/γHS最大值，两侧波压力很快减小，向上波压力降低较快，向下波压力降低较慢，这种变化规律和以往的室内研究成果是一致的。

图1 波压力沿斜坡变化的示例Fig.1 The example of wave pressure along the slope

图2 所有组次ps/γHS～x/L的关系Fig.2 The relationship between ps/γHSand x/L in all cases

1.4 最大相对波压力与波坦、水深的关系

由图3(a)可见最大相对波压力是随着波坦的增大呈现增大的趋势。波坦小于25时最大相对波压力随波坦增大而增大的幅度较大，随后增大的趋势减缓。由图3(b)可见最大相对波压力是随着相对水深的增大呈现增大的趋势。

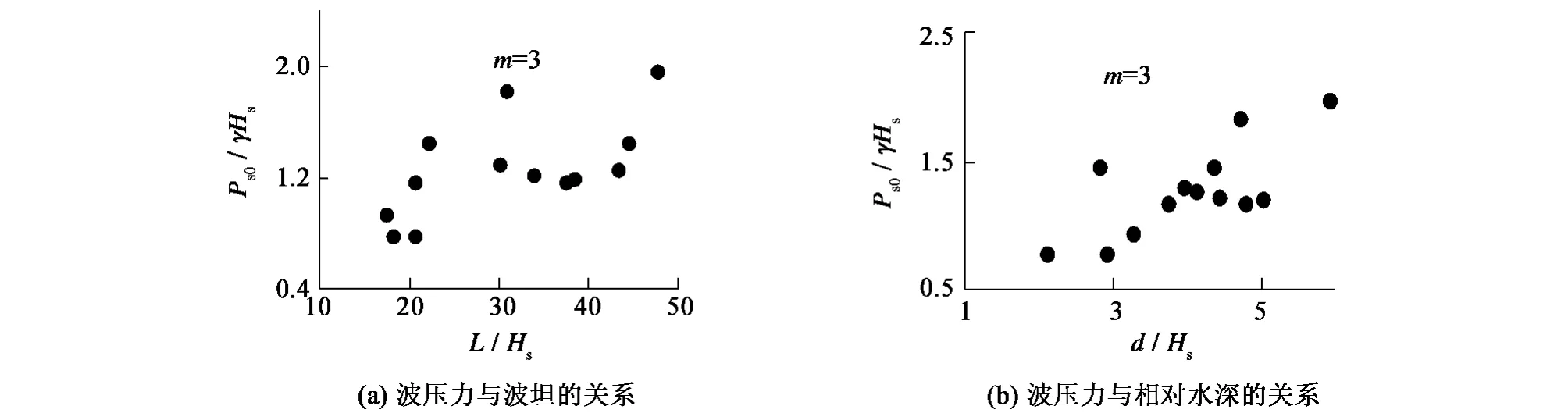
图3 最大相对波压力随波坦和相对水深的变化示意Fig.3 Change of maximum relative wave pressure with wave flatness and relative water depth

2 不规则波室内试验

2.1 试验设备、采样和资料整理方法

斜坡波压力的试验是在长80.0 m×1.0 m×1.2 m(长×宽×高)水槽内进行。水槽中后部的试验段将水槽分隔成等间距的两部分，外侧水槽安放试验断面。水槽的一端设有液压式推板造波机。本试验中波压力的采集使用的是Dj800型多功能数据采集及处理系统和直径为2 cm的压力传感器。不规则波每组波列的持续时间约为5.0～6.0 min，波数约为120～150个左右，待水面平静后进行下一组试验，每组试验重复三次。

试验的断面形式为单坡，模型中堤面采用不透水的厚度为2 cm的硬塑料板。为了保证护面板的刚度，护面板下侧钢架由两条角钢和四排钢横杆组成，并在两侧加了四条可调节长度的角钢支撑杆。

为了较准确测到最大压力点位置，在模型中布置测压点的位置时，静水位点处附近以及沿斜坡在静水位向下一定距离内尽可能密集布置测压传感器，斜面上一般布置15～19个压力传感器。

本次试验的期望谱选用JONSWAP谱，谱峰参数γ=3.3，试验中取堤前水深d=30 cm、40 cm，坡度m=2、3、4，相对水深 d/HS=5.0、4.0、3.0、2.5、2.0，波坦 L/HS=15、20、25、30、40，在对采集的波压力数据进行分析时，采用波压力的峰值作为波压值，以冲击压峰值的1/3大值的平均值记为ps，斜坡面上冲击压力最大值记为 ps0。

2.2 最大冲击力试验成果分析

2.2.1 波坦L/HS对最大打击力的影响

试验表明在不规则波作用下，ps0/γHS随波坦变化比较复杂，以m=3，d=40 cm情况为例(图4(a))，当d/HS=2.5、3.0 时，ps0/γHS有随着波坦 L/HS增大而增大的趋势;当 d/HS=4.0、5.0 时，随波坦增大，ps0/γHS开始减小，之后又出现增大。关于波坦对最大打击力的影响，现有的室内试验结果并不一致，其变化规律与坡度、相对水深均有关系。呈现比较复杂的交错状态。本结果与现场观测资料对比，变化规律也有差异，现场资料是包含不同相对水深条件下测得的结果，与室内试验条件是不同的。

2.2.2 坡度的影响

试验表明:对不同波坦、不同相对水深d/HS以及相对波压强ps/γHS随坡比m变化而变化的情况十分复杂。对于L/HS=15、20，当相对水深较大时，多数情况下相对波压强随m增大呈先增大后减小，在m=3时出现最大值;对于L/HS=25、30，当m增大时，相对波压强ps/γHS变化的峰值不甚明显，有的单一增大趋势，有的呈单一减小趋势，也有在m=3时出现峰值的;对L/HS=40，多数情况是随m增大，相对波压强略有减小。总之，m变化对ps/γHS的影响很难用单一参数来描述。由于这里只取三个坡度反映坡度变化受到限制。钟瑚穗曾在较大坡度范围进行坡度影响的试验，并且得出存在最大波压的临界坡度，对不同波坦出现最大波压的临界坡度是不同的。

2.2.3 相对水深d/HS的影响

图4(b)可见，不规则波的作用下最大相对波压力基本随着相对水深的增大而增大，随着坡度的减缓这种关系越是明显。但是当L/HS≥30和m=2时，相对最大波压力却是随着相对水深的增大而略有减小。

图4 m=3，d=40 cm时最大相对波压力随波坦和相对水深的变化Fig.4 Change of maximum relative wave pressure with wave flatness and relative water depth when m=3，d=40 cm

2.2.4 波压力沿斜坡的分布

波压力沿整个斜坡面分布极不均匀，打击点压力最大，随着离开打击点两侧的压力急剧衰减，以最大波压力打击点位置为分界点，在最大打击点位置右边波压力衰减程度明显比左边来的大。图5为d=30 cm，d/HS=4时三个坡度的波压力沿斜坡分布图，图中横坐标原点在静水面处。

3 波浪冲击力的计算方法

3.1 最大值及作用点位置公式

为了考虑各因素对波浪冲击力的综合影响，引入伊里巴伦数ξ来拟合最大相对波压力ps0/γHS的包络线。伊里巴伦数又称破波参数，由入射波高，波长和斜坡坡度组成:

图6是莆田试验站实测资料和室内试验的最大相对波压力ps0/γHS～ξ的相关图，最大相对波压力随ξ的变化其实就是从缓坡到陡坡再到直墙的变化过程中相对波压力的变化。从图形的顶点处对应的破波参数为对应点ξ=1.36，在0.97≤ξ＜1.36区段大体上为缓坡情况，随着ξ的增大相对最大波压力增大。在1.36≤ξ≤3.16区段大体上为陡坡情况，随着ξ的增大相对最大波压力逐渐减小，但是减小的幅度慢慢变小，最后应趋近于一个数值。这是由于ξ很大时，斜坡坡面趋近于直立面的缘故。

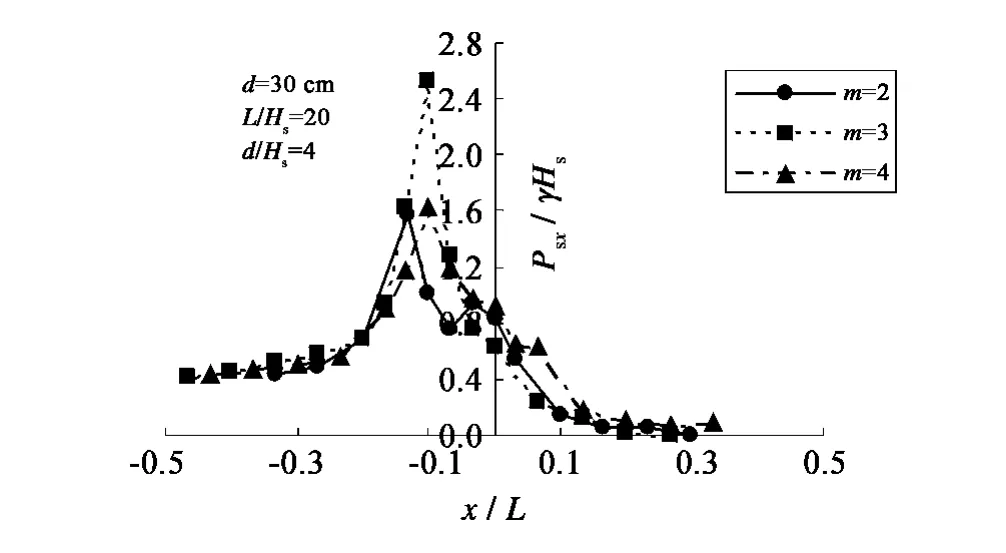
图5 m=2，d=30 cm时波浪冲击压力沿斜坡分布Fig.5 Wave pressure along the slope when m=2，d=30 cm

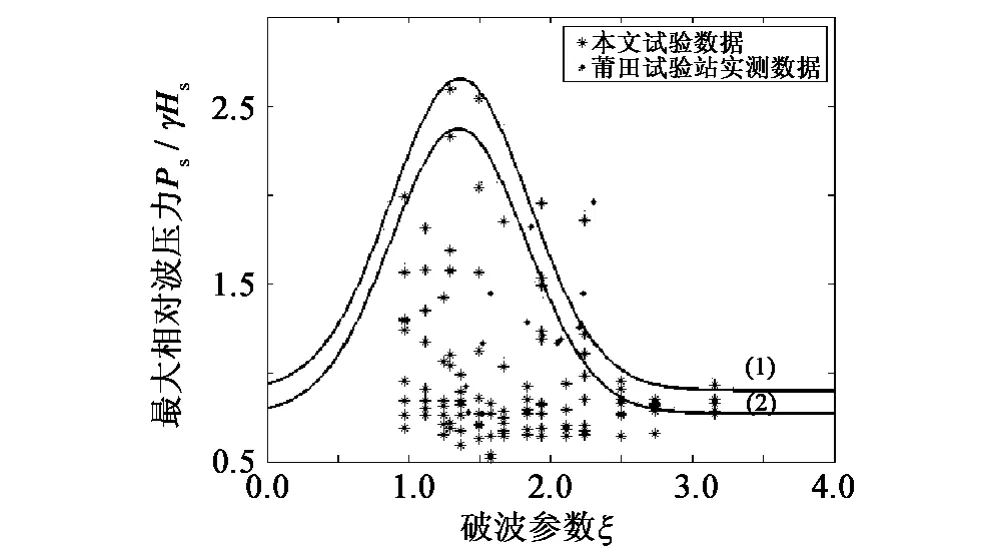
图6 最大相对波压力包络线拟合曲线Fig.6 The envelop of maximum relative wave pressure

根据资料可得到最大相对波压力ps0/γHS与伊里巴伦数的拟合公式:

式(2)拟合曲线接近试验点外包络线，式(3)相当于90%的试验点小于拟合曲线值，一般情况可采用式(3)计算。式(2)、(3)在ξ=1.36时，最大相对波压力取极值，相当于卷破波破碎时比较剧烈作用的情况。试验参数的变化范围:ξ=0.97 ～3.16，m=2 ～ 4，L/HS=15 ～40，d/HS=2 ～5。

以王鉴义［3］文中的算例作一比较，计算条件为 HS=1.34 m，L=26.08 m，d=10 m，m=3 的单坡堤，由于计算通常采用p1%，故用p1%进行比较。按前苏联规范可得最大打击压力p1%=45.9 kN;按王鉴义方法可得ps=43.4 kN，p1%=51.2 kN;按式(3)可得 ps=29.1 kN，p1%=51.2 kN。

对于最大冲击波压力在斜坡上的位置，试验表明波坦的影响较小，与相对水深和坡度有一定关系，文中忽略波坦对打击中心点位置的影响，考虑相对水深和坡度的影响，利用Matlab软件对最大压力点相对深度进行拟合，得出打击中心点相对位置公式:

式中:e0为波浪最大冲击力在静水位下的竖直深度。

3.2 波压力的统计分布

采用韦伯分布、对数正态分布对室内试验的相对波浪冲击力ps0/γHS进行拟合优度检验，用最大似然法求其分布的参数值，再用K-S假设检验验证其是否符合假定分布。结果表明对数正态分布优于韦伯分布，参与统计分布的组次共有351组，对数正态分布通过检验的有322组，通过率为91.7%。得到通过组数中参数μ在-0.05～-0.3之间，参数 σ 在0.3～0.7之间，将所用通过组次的参数平均不同累积频率下的波压力换算关系列于表1。对莆田试验站资料仅进行统计特征值计算，其主要结果和室内试验比较如表2所示。

表1 波压力在不同累积频率下的换算关系Tab.1 The conversion coefficient of different cumulative frequencies

表2 相关压力统计特征值表Tab.2 Statistical characteristic values of related wave pressure

对照表1和表2，通过统计适度检验采用理论分布得出p1%/p1/3的与莆田站实测的p1%/p1/3尚接近，但与室内试验结果差别较大。根据一些室内试验研究，如李翔［8］得出p1%/p1/3与破波参数ξ有关，实测值变化在1.1～4.0之间;钟南艳［3］根据分布检验，由理论分布得出的变化范围在1.36～1.77之间。表2中室内试验的pm值是一组试验(120～150个波)的波压最大值，大于p1%。

无论现场观测还是室内试验，由于试验数据的随机性，直接从有限的试验数据得出的统计特征值较不稳定，故建议按数理统计方法得出的理论分布的换算系数。

3.3 波压力沿斜坡分布公式拟合

在进行强度计算时需确定波压力沿斜坡分布。以最大相对压力打击点(最大压力点)为坐标原点，可做出波压力沿斜坡的相对距离x/L的变化图，为计算方便纵坐标采用psx/ps0，psx表示沿打击点两侧相对距离为x/L处波压ps，ps0为最大压力冲击点o点的ps，图7是m=3，d=30 cm的psx/ps0～x/L的相关图。

假定选取式(5)、(6)曲线形式来拟合波压力沿斜坡的分布的包络图规律:

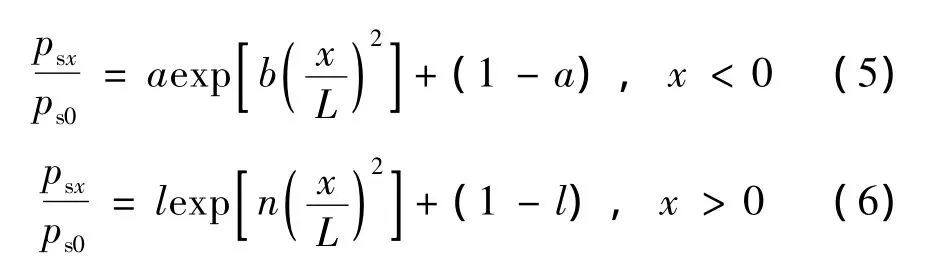
式中:左侧指向水下方向x/L，取负值;右侧指向水上方向x/L，取正值。基于Matlab数学软件平台，根据实测试验数据拟合出psx/ps0与x/L的关系曲线得出待定系数如表3所示。

由表3可见，m变化时，系数变幅不是很大，因而从简化计算出发，采用系数的平均值，可得相对波压力沿斜坡分布的拟合曲线公式:

图7 m=3时psx/ps0与x/L拟合包络曲线Fig.7 The envelop of wave pressure along the slope when m=3

式中:x是不同条件下以最大压力冲击点为起点的沿斜坡的距离，取向上为正。

表3 坡度m与各系数的关系Tab.3 The relationship between slope m and coefficients

4 结语

通过莆田试验站实测资料整理分析和室内不规则波对单一斜坡护面板的打击力试验分析，结果表明:

1)波浪打击斜坡面瞬时在静水位至水面下1.0HS范围内出现最大冲击力，冲击点处相对波压力ps0/γHS可达2.6左右。

2)波浪最大冲击力两侧压力很快衰减，其中向上一侧波压衰减较快，两侧波压力分布包络线可采取负指数函数表示。

3)相对最大冲击力ps0/γHS和波坦、坡度的关系不是单调变化的，而是呈较复杂的交叉状态。ps0/γHS～ξ的相关图包络线可采用指数函数表示。

4)统计检验表明最大冲击力符合对数正态分布。

5)这里建议的方法是在m=2～4，L/HS=15～40，d/HS=2～5的条件得出的。

［1］潘少华.混凝土板护坡的防浪特性［J］.上海水利，1996，S1:103-113.

［2］潘少华，译.波浪、冰凌和船舶对水工建筑的荷载与作用(СНиПⅡ57-75)［M］.北京:海洋出版社，1986.

［3］王鉴义，章家昌，周家宝，等.不规则波对平板护面单坡堤的波压力试验研究［J］.海洋工程，1996，14(4):22-29.

［4］钟南艳.斜坡堤护面板的波浪打击力研究［D］.南京:河海大学，2009.

［5］Alfred Fühböter.Model and prototype tests for wave impact and run-up on an uniform 1:4 slop［J］.Coastal Engineering，1986，10(1):49-84.

［6］Neelamani S，Schüttrumpf H，Muttray M，et al.Prediction of wave pressures on smooth impermeable seawalls［J］.Ocean Engingeering，1999，26(8):739-765.

［7］钟瑚穗.波浪冲击压力理论和模比影响的研究［J］.河海大学学报，1988，16(2):20-28.

［8］李 翔.不同开孔率混凝土护面波浪打击力和爬高试验研究［D］.南京:河海大学，2010.

Experimental study of wave impact pressure on the protection slab of uniform slope and field data analysis

FENG Wei-bing1，ZHANG Hui1，HAO Qing-ling2
(1.College of Harbor，Coastal and Offshore Engineering，Hohai University，Nanjing 210098，China;2.Zhanjiang Design Institute of South China Sea Fleet，Zhanjiang 524003，China)

The wave impact pressure of irregular waves on protection slab of uniform slope is studied by use of some wave pressure data measured at on-site experiment stations in Putian last century and recent physical model tests.Base on the test results，the influencing factors are presented.Experimental formulas of maximum impulsive pressure，water depth of maximum impulsive pressure and wave pressure along the slope are proposed.The conversion coefficient of different cumulative frequencies is got by counting and analyzing the impact pressure of irregular waves on the protection slab.

irregular wave;uniform slope;wave impact pressure;wave pressure;Putian

U656.1

A

1005-9865(2012)04-0097-06

2011-06-30

冯卫兵(1960-)，男，博士，教授，主要从事波浪方面的研究工作。E-mail:wbfeng60@126.com