水深对系泊起重船运动影响的数值与试验分析

董 璐，徐 慧，高 巍，骆寒冰

(1.天津大学建筑工程学院，天津 300072;2.北京高泰深海技术有限公司，北京 100011)

水深对系泊起重船运动影响的数值与试验分析

董 璐1，徐 慧1，高 巍2，骆寒冰1

(1.天津大学建筑工程学院，天津 300072;2.北京高泰深海技术有限公司，北京 100011)

以一艘现役起重船为研究对象，对其进行不同水深(46 m和36 m)，缩尺比1∶50的模型试验。采用基于二次传递函数QTF的时域准静态分析法对实际尺度起重船与系泊系统进行耦合数值分析，并与试验结果进行比较。结果表明，当水深变浅时，浅水对二阶载荷的影响是系泊力明显的主要因素，浅水对一阶载荷的影响有限。在保持系泊系统刚度线性不随水深变化的前提下进行了三个水深吃水比的数值模拟计算，结果表明，对于系泊起重船，随着水深的减小，二阶定常力有所增大;浅水对差频载荷的影响在30 m水深(吃水水深比d/h=0.27)时变得明显。对于浅水系泊系统的相关分析需要充分考虑水深对二阶慢漂运动的影响，保证系泊系统的安全。

起重船;系泊系统;模型试验;数值分析;水深影响

起重船是海洋工程领域中不可缺少的工程船舶。有限水深下，起重船系泊运动的稳定性、系泊系统的安全性对起重船相关作业有着重要作用。影响系泊起重船运动响应的主要载荷是二阶波浪载荷中的二阶定常载荷与二阶差频载荷。

浅水系泊的相关研究多集中在浅水作业的FPSO、穿梭油轮、LNG船等方面［1-4］，浅水对系泊系统安全的影响因素有浅水波影响及一阶载荷与二阶载荷的浅水效应等方面，其中二阶差频载荷由于与系泊系统固有周期较为接近，对系泊系统安全有着重要影响，是相关研究的热点之一。

二阶差频载荷由海浪中两个不同频率的成分波相互作用产生，可通过二次传递函数QTF(quadratic transfer function)来进行计算。QTF主要由一阶速度势引起的二阶量和二阶速度势引起的一阶量两部分组成。有限水深条件下，二阶速度势量对差频载荷的影响不可忽视［5］。

为了考察水深变化对系泊起重船慢漂运动的影响，以一艘作业水深变化的现役起重船为研究对象，在天津大学建筑工程学院港口与海岸工程水池进行多点系泊状态下，水深分别为46 m、36 m的模型试验，缩尺比为1∶50。采用基于全QTF法的时域准静态分析法对实尺度系泊起重船进行数值分析，研究随水深变化的系泊起重船运动性能与系泊力。

1 模型试验

1.1 不规则波参数、系泊系统与起重船参数

起重船主要参数:垂线间长153.5 m，船宽48 m，型深12.5 m，吃水8 m。试验包括静水试验，规则波试验和不规则波试验三部分。表1为不规则波主要参数，从表1中可以发现造波机造波情况良好，符合要求。规则波波长范围为0.3～2.0倍船长，经比较发现规则波试验中的波浪均为有限水深波，排除了浅水波的影响。图1为系泊系统布置示意图，系泊系统由八根钢丝缆组成，预张力17 t，船艏指向x正方向，左舷指向y轴正方向。

表1 不规则波主要参数Tab.1 The main parameters of irregular wave

造波机造可依照JONSWAP谱造不规则波，JONSWAP谱表达式为

式中:Sζ(ω)为谱密度;ω为圆频率;HS为有义波高;γ为形状参数，由于本起重船多在南海、东海进行相关作业，为了尽可能贴近实际作业海域海况条件，取γ=1;T1为谱峰周期。

1.2 系泊系统刚度

图2为系泊系统刚度试验值与理论值比较。各个工况下系泊缆预张力相同，随着水深的减小，系泊系统的刚度有所增加。系泊系统的回复力与位移关系符合线性规律，46 m水深系泊系统刚度为22.41 t/m;36 m水深系泊系统刚度为24.65 t/m。试验中系泊系统刚度情况与理论计算结果非常接近。

图1 系泊布置示意Fig.1 The arrangement of mooring system

图2 不同水深系泊系统刚度情况Fig.2 The mooring stiffness with different water depths

2 数值计算与试验结果的对比

2.1 数值模型及求解

二次传递函数QTF是由一阶速度势的二阶产物和二阶速度势影响两部分组成，即［1］:

QTF表达为两个相互影响的成分波频率的函数:

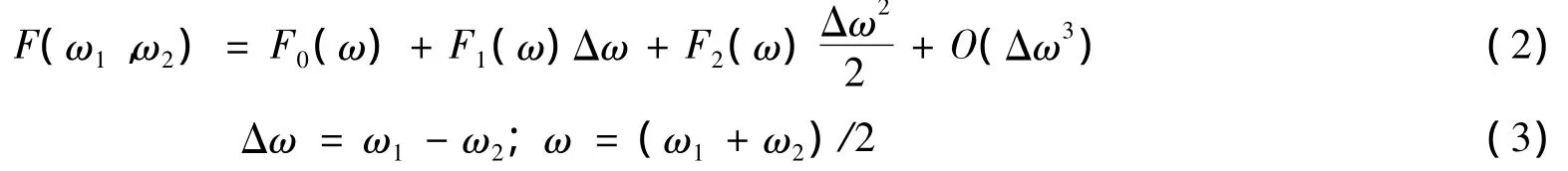
式中:ω1，ω2为两相互影响的成分波频率;F0(ω)是依赖于ω的实函数，即二阶定常力;F1(ω)是与Δω呈线性比例关系的虚函数;F2(ω)与Δω2呈比例的复函数［4］。

Newman近似法通过F0(ω)估算QTF。有限水深条件下，使用Newman近似法将低估二阶差频载荷［6-8］，这对于系泊安全分析是不利的。数值模拟计算中使用全QTF法计算二阶慢漂载荷。

图3为起重船水动力计算模型。使用三维势流理论进行水动力求解，采用近场法求解二阶定常载荷。为了改善尖角处计算结果的收敛性，对尖角处单元进行了手动修改，最终建立的水动力模型面元总数为709。二阶慢漂载荷采用全QTF法进行求解。重心、回转半径等参数保证与试验一致。

系泊系统与浮体耦合分析模型如图4。由于波高较小，试算发现起重船的运动幅值较小，此时锚泊阻尼与缆绳动力响应对于最终结果的影响较为有限［8］，因而采用时域准静态法求解耦合方程，以减少计算时间。

图3 起重船水动力模型Fig.3 Hydrodynamic model of the crane ship

图4 耦合分析模型Fig.4 Coupled analytical model

2.2 数值计算结果与试验结果对比分析

图5为46 m、36 m水深下起重船迎浪纵荡、垂荡、纵摇RAO计算值与试验值比较。随着水深由46 m变为36 m:纵荡RAO在0.5 rad/s后的值有所增加;垂荡RAO高频处并无明显的变化，低频处结果有所下降;纵摇固有频率变小，大于固有频率的范围内RAO值有所减小，小于固有频率的范围内RAO值有所增加。总体来说，随着水深由46 m变为36 m，浅水对起重船垂荡、纵摇一阶运动的影响较小，对纵荡运动影响较大。

为了进一步考察水深变化对起重船迎浪RAO的影响，对30 m、50 m和100 m水深下的起重船纵荡、垂荡、纵摇进行了数值计算，结果比较如图6。从图6可以发现，随着水深的变浅:纵荡RAO在低频处(ω＜0.3 rad/s)逐渐增高，在0.6 rad/s＜ω＜0.8 rad/s区域有所增加，这与试验结果是一致的;垂荡RAO在ω＜0.6 rad/s区域逐渐减小，位于0.6 rad/s＜ω＜0.8 rad/s区域的峰值有向低频移动的趋势;纵摇RAO在ω＜0.6 rad/s区域逐渐增大，且该频率范围内的峰值向低频移动，这一点在试验中也有所体现。总的来说，随着水深的变浅，迎浪下起重船的纵荡、垂荡、纵摇RAO在频率较低的区域(ω＜0.6 rad/s)有明显的变化，纵荡、纵摇RAO有增大的趋势，垂荡RAO有减小的趋势;垂荡、纵摇RAO的峰值随着水深变浅均有向低频区域移动的趋势。

表2为46 m、36 m水深下，系泊起重船运动响应与系泊力计算结果与试验结果比较情况。随着水深由46 m变为36 m，系泊力有义峰谷值增大10%，低频系泊力的增加是最主要的影响因素;纵荡、垂荡、纵摇的波频运动结果并无明显变化，这与RAO比较结果是一致的;纵荡运动低频有义峰谷值并无明显变化，考虑到36 m水深下纵荡系泊刚度较大，因而推断刚度一致情况下纵荡低频运动随着水深变浅会有较明显变化;运动计算结果与试验结果较为符合，纵荡计算结果有所偏差，纵摇与垂荡计算结果较为可信;系泊力计算结果均比试验值偏大，从工程的角度讲该计算结果是偏于保守的。

表2 46 m和36 m水深系泊起重船运动响应与系泊力计算结果与试验结果比较Tab.2 Results of the experimental and numerical analyses with 46 m and 36 m water depths

图5 迎浪46 m和36 m不同水深下起重船RAOFig.5 Crane ship head sea RAO

图6 迎浪30 m、50 m和100 m不同水深下起重船RAO比较Fig.6 Crane ship head sea RAO with different water depths

3 二阶差频载荷的水深敏感性分析

对起重船吃水8.0 m，三个不同吃水水深比(水深分别为h=100 m，50 m，30 m，吃水水深比d/h=0.08，0.16，0.27)下的系泊运动进行数值分析计算。系泊系统是这样布置的:在船的四周各有一根线弹性绳，与船呈90°角，缆绳的刚度为1.47×105N/m;缆绳斜向外延伸50 m，不与自由表面接触(如图7)，保证整个系泊系统的刚度是线性的并且不随水深变化。

波浪环境条件为JONSWAP谱描述，其中 γ=1.0，有义波高 HS=6.50 m，谱峰频率 Wp=0.495 rad/s，波向为迎浪。

不同水深下系泊起重船的运动响应统计值，低频运动响应值，波频运动响应值及平均飘逸距离结果分别如表3、4。从表3可以发现:随着水深的变浅，系泊浮体纵荡运动有了明显提高，纵摇和垂荡运动变化不大，其他自由度均不同程度的减小;随着水深的变浅，系泊浮体纵荡低频运动增加较为明显，垂荡、纵摇运动有所增加，其他自由度低频运动有所减小。综合来看，随着水深的变浅，二阶浅水响应对差频载荷的影响逐渐显现，在30 m水深，吃水水深比d/h=0.27时有了较为明显的提高。从表3可以发现:水深变浅，系泊浮体的波频运动变化并不明显，由此可见浅水对一阶载荷的影响并不是影响系泊浮体运动的主要因素，这与试验结果也是吻合的。从表4可以发现:由于系泊浮体的初始位置一定，随着水深变浅，系泊浮体的最终漂移距离加大，因而可以推断随着水深变浅，二阶定常力有所增加。

图7 水深敏感性数值分析模型Fig.7 Water sensitivity numerical simulation model

表3 不同水深下系泊起重船相关运动响应二倍均方值比较Tab.3 Twice the mean square value results of the numerical analysis with different water depths

表4 不同水深下系泊起重船平均漂移距离对比Tab.4 The average offset distance numerical analysis results with different water depths

4 结语

以一艘现役起重船为研究对象，进行了不同水深(分别为46 m和36 m)系泊状态下模型试验，使用基于全QTF法的时域准静态法进行了数值计算，通过比较得出如下结论:

当水深由46 m变为36 m时，系泊力有较明显的增加，浅水对二阶载荷的影响是主要因素，浅水对一阶载荷有所影响，但是影响程度非常有限。通过比较30 m、50 m、100 m水深下起重船迎浪纵荡、垂荡及纵摇RAO，发现浅水对起重船一阶运动的影响主要位于频率ω＜0.6 rad/s的区域，且纵荡、纵摇RAO有增大的趋势，垂荡RAO有减小的趋势;垂荡、纵摇RAO的峰值随着水深变浅均有向低频区域移动的趋势。

在保持系泊系统刚度为线性且不随水深变化前提下，对起重船进行了三个水深(100 m、50 m、30 m，吃水水深比d/h对应为0.08、0.16、0.27)下运动响应数值计算。对于起重船船型，随着水深减小，二阶定常力有所增大;二阶浅水响应对差频载荷的影响在30 m水深，吃水水深比为d/h=0.27时变得明显;浅水对一阶载荷的影响并不是影响系泊浮体运动的主要因素;50 m水深，吃水水深比为d/h=0.160时水深对二阶差频载荷的影响较小。

对于浅水系泊系统的相关分析需要充分考虑水深对二阶慢漂运动的影响，保证系泊系统的安全。

［1］肖龙飞.浅水波及软刚臂系泊FPSO浅水效应研究［D］.上海:上海交通大学，2007.

［2］肖龙飞，杨立军，杨建民.软刚臂系泊系统水平恢复力特性数值预报［J］.海洋工程，2008，26(1):24-28.

［3］史琪琪，杨建民.半潜式平台运动及系泊系统特性研究［J］.海洋工程，2010，28(4):1-8.

［4］Naciri M，Buchner B，Bunnik T，et al.Low frequency motions of LNG carriers moored in shallow water［C］∥Proc.of the 23rdInt.Conf.on Offshore Mechanics and Arctic Engineering.2004，3:995-1006.

［5］Chen Xiao-Bo，FlaviaRezende.Efficient computations of second-order low-frequency wave load［C］∥Proceedings of the ASME 28th International Conference on Offshore Mechanics and Arctic Engineering.2009:OMAE2009-79522.

［6］Chen Xiao-Bo.Approximation on the QTF of low freq loads［C］∥Proc.Boss’94.1994:289-302.

［7］Jo˜ao Pessoa，Nuno Fonseca，C Guedes Soares.Experimental and numerical sludy of the depth effect on the first order and slowly varying motions of a floating body in bichromatic waves［C］∥Proceedings of the ASME 29th International Conference on Offshore Mechanics and Arctic Engineering.2010:OMAE2010-21188.

［8］Jo˜ao Pessoa，Nuno Fonseca，C Guedes Soares.Drift force om a floating body of simple geometry due to secong order interactions between pairs of harmonics with different frequences［C］∥Proceedings of the ASME 2009 28th International Conference on O-cean，Offshore and Arctic Engineering.2009:OMAE2009-80225.

Numerical simulation and experimental comparison about water depth’s influences to moored floating crane ship

DONG Lu1，XU Hui1，GAO Wei2，LUO Han-bing1
(1.Department of Naval Architecture，Tianjin University，Tianjin 300072，China;2.COTEC Offshore Engineering Solutions，Beijing 100011，China)

Taking a multi-point moored floating crane ship as an example，a model test at 46 m and 36 m water depth is performed with model scale 1:50.Based on full QTF method，an actual scale time domain quasi static numerical simulation is done and compared with model test value.The results show that with the water depth decreasing，the shallow water effect on second-order load is the major reason for mooring force increasing，and the shallow water effect on the first-order load is very limited.Maintaining the mooring system stiffness is linear and does not vary with water depth，and a numerical simulation is done with three draft depth ratio.The results show that for moored crane ships，as water depth decreases，the second-order steady force increases，and the shallow water effect on slowly drift load becomes apparent in 30 m water depth(draft depth ratio d/h=0.27).For shallow water mooring analysis，the second-order shallow water effects should be fully considered to ensure the safety of mooring systems.

floating crane ship;mooring system;model test;numerical simulation;water depth effect

U661.73

A

1005-9865(2012)04-0125-06

2011-12-08

董 璐(1987－)，女，主要从事船舶工程方面的研究。E-mail:donglujane@163.com

志谢:感谢BV船级社的软件支持。