中国证券市场非线性结构的实证检验

邹裔忠

（武夷学院，福建 武夷山 354300）

中国证券市场非线性结构的实证检验

邹裔忠

（武夷学院，福建 武夷山 354300）

用BDS统计量进行实证检验，找到了我国证券市场对数收益率序列存在非线性结构的证据，并且通过稳定性分析和线性过滤后的BDS统计量检验，排除了由非平稳和线性依赖产生非线性结构的可能。说明我国证券市场的非线性结构类型只能是混沌或非线性随机过程。

BDS统计检验；非线性结构；混沌

现代金融经济学建立在理性经济人的假定基础上，证券价格能够快速地调整以反映任何新的公开得到的信息的“有效市场假说”成为其重要基石。但是大量实证支持收益率具有尖峰肥尾特征的非正态分布、自回归条件异方差 （ARCH）现象和长期记忆等非线性，经济学者开始反思以线性、理性和秩序为特征的研究范式。

BDS统计量是检验非线性性的主要方法，国内外学者在股票、期货、利率和汇率中都找到非线性的证据。Scheinkman和LeBaron（1989）对芝加哥大学证券研究中心（CRSP）的价值加权组合的周股票收益进行研究，BDS检验表明了检验数据是非线性的，并且可能是混沌的[1]。Hsieh在1989年对美元、英国英镑、加拿大元、德国马克、日本日元和瑞士法郎之间的汇率进行了BDS检验，他在汇率中发现了强烈的非线性[2]。王明进（2000）应用BDS检验分析纽约商品交易所3个月期货铜的日收盘价从1991年10月3日到1995年11月29日共1025天的数据，发现其中具有强烈的非线性结构[3]。但是，目前文献中只检测出存在非线性特征，没有判断存在何种类型的非线性结构。本文通过BDS统计量进行实证检验，并确定其非线性结构的类型。

一、BDS统计量

BDS统计量是 1987年由 Brock、Dechert和Scheinkman提出的一个检验统计量，用来检测一个时间序列的独立同分布假设。与其他讨论过的检验统计量主要集中在时间序列的2阶或3阶性质上不同，BDS统计量是基于相关维数估计设计出来的，能够探测其它一些统计检验所忽视的非平稳性、非线性性，因而在非线性检验中具有很强的功效性[4]。

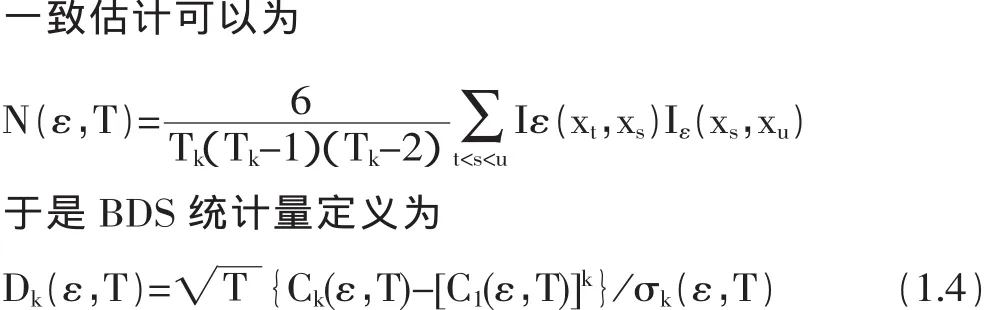
其中 σk（ε，T）是用 C1（ε，T）和 N（ε，T）分别代替 C和N时通过σk（ε）得到的。这个检验统计量的极限分布是标准正态的。该定义方式能检验出几乎所有的线性和非线性、随机的和确定性的时间序列，不幸的是，这种工具要求密集处理以及有效的计算机算法使它在相对小样本数据集上可行。Kanzler（1999）提出了一种非常快的、相当简单并且在普通程序环境下容易应用的算法[5]。其算法被设计成Eviews中的BDS检验工具，本文用这一方法来实证。

二、数据来源与处理方法

本文选取1992年2月1日至2008年6月30日的上证综合指数的日数据（记为shd）和周数据（记为shw），1991年5月1日至2008年6月30日的深证成份指数的日数据（记为szd）和周数据（记为szw），构建两个不同时间频率的时间序列。由于中国期货市场起步较晚，选取大连商品期货市场的黄大豆一0907的价格指数（记为dd）和郑州商品期货市场的硬麦连3的价格指数（记为ym）从1999年1月4日至2008年6月30日的数据，上海期货交易所的铜3月的价格指数（记为 cu）从 1995年 7月 14日至2008年 6月 30日的数据。数据全部来源于Wind资讯金融终端。

传统的有效市场理论认为对数收益率满足正态分布，本文使用对数收益来检验我国证券市场的非线性性，能更好体现非线性性对传统经典金融理论的冲击。资产的连续复合收益或对数收益定义为：

三、BDS统计量对非线性结构的检验

BDS统计量对嵌入维数k和维数距离ε的选取很敏感，Brock等（1993）检查了BDS统计量的有限样本分布发现：当样本有500或者500以上个观测值，嵌入维数k为5或者更低时，ε为0.5、1.0、1.5和 2.0倍数据标准差时，渐近分布能够较好地估计统计量分布[6]。 Kanzler（1999）的研究认为，嵌入维数 k从2取到15，ε为1.5倍标准差时，检验效果较好[5]。本文选取的样本数大多都大于2000个观测值，所以，对样本进行BDS检验时，嵌入维数k从2取到15，维数距离ε取1.5倍标准差，可以达到较好的检验效果。Eviews5.0软件根据Kanzler（1999）的算法设计出了BDS检验工具，本文用此软件进行实证研究。

检验结果见表1，可以看出BDS统计量均大于正态分布在5%显著性水平下的临界值1.96和1%显著性水平下的临界值2.58。BDS统计量提供了拒绝独立同分布（i.i.d.）的原假设的证据，说明我国证券市场的非线性结构。日数据的BDS统计量大于周数据，反映出日数据具有更为显著的非线性特征；股票日数据的BDS统计量大于期货日数据的BDS统计量，说明股票的非线性结构更为显著。

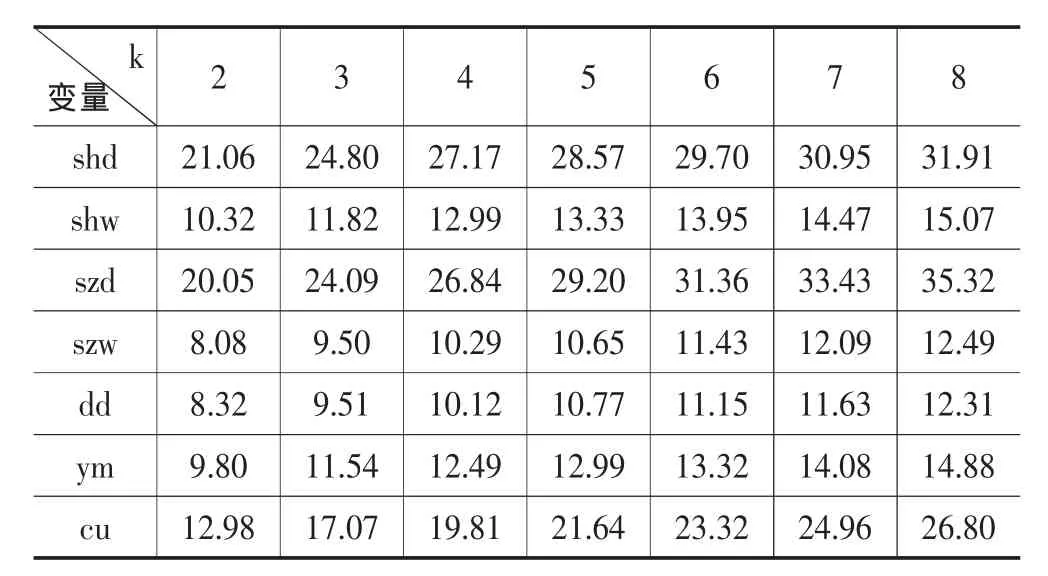
表1 证券收益率的BDS独立同分布检验 ε／σ＝1.5

BDS检验的不足在于不能判断存在何种类型的非线性结构。Hsieh（1991）通过模拟，BDS检验具有较好的功效来判断四种类型的非i.i.d.行为：线性依赖、非平稳、混沌和非线性随机过程，那么拒绝原假设，说明我们所研究的序列可能会是四种情形的任何一种[2]。以下内容就对这四种非线性结构进行分析。

四、平稳性分析

在经济上，非平稳是和结构性变化同步的，能够引起结构发生变化的原因有多种，可以是技术和金融创新，还可能是政策改变等其它原因。中国的证券市场也经历了许多次的深层次的结构变化，显然需要进行平稳性分析。

表2 证券收益率的平稳性检验

对于平稳性检验，我们这里考虑的主要是协方差平稳，即弱平稳。检验一个序列的平稳性，传统的检验方法是增广Dickey-Fuller检验（ADF检验），然而由于被分析的价格序列可能会包含异方差，这时我们借助于考虑到序列相关和异方差的Phillips-Perron（PP检验）的非参数检验。ADF和PP都用单位根作为原假设。

通过ADF检验和PP检验，从表2可以看出，检验值都很大，对应的p值都近似为0.00，有较强的证据拒绝单位根的原假设，说明所检验序列都是平稳的，这就排除了由非平稳引起的非线性结构的可能性。

五、经AR（p）模型线性过滤后的BDS检验

为了排除BDS检验显著拒绝i.i.d.是由证券收益率的线性依赖这一因素引起的可能，我们先用AR（p）模型对原始收益率序列进行线性过滤后，对其残差进行BDS检验，并与过滤前的BDS检验进行对比。

用经典的AR（p）线性模型对证券市场收益率序列进行拟合，滤去线性相关的成份，拟合结果如表3，阶数p的选取可以用偏自相关函数（PACF）方法，对一个AR（p）模型，间隔为p的样本的PACF不应为零，而对所有大于pp的参数应接近于零。用Ljung和box的Q统计量对收益率序列的线性相关性进行检验，通过过滤前后Q统计量的对比，来检验线性过滤的效果[7]。

表3 证券收益率的线性过滤的AR(p)模型

Q 统计量首先由 Box、Pierce（1970）提出的，后来，Ljung、Box(1978)提出一个在小样本条件下具有更好近似性质的修正Q统计量。k阶滞后的Q统计量的零假设是序列没有 k 阶的自相关，即：ρ1=ρ2=…=ρk＝0。 如果序列不是以ARIMA估计的结果为基础，在原假设下，Q 统计量是渐近 χ2（k）分布，即：

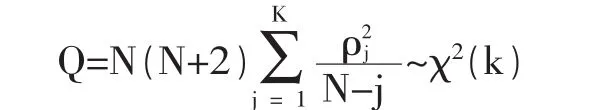
用Ljung-Box的Q统计量检验线性过滤效果如表4，因限于篇幅，表中只给出了部分滞后阶数的检验结果。表中可以看出证券收益率的原始序列的Q统计量对应的p值大部分为0.00，有较强的理由拒绝没有k阶的自相关的原假设，说明收益率原始序列存在强较的线性相关性。而经过AR（p）线性模型过滤后，其残差序列的Q统计量均小于临界值，其p值大部分都超过20%，说明AR(p)模型已经过滤掉了证券收益率序列中的线性相关成份。

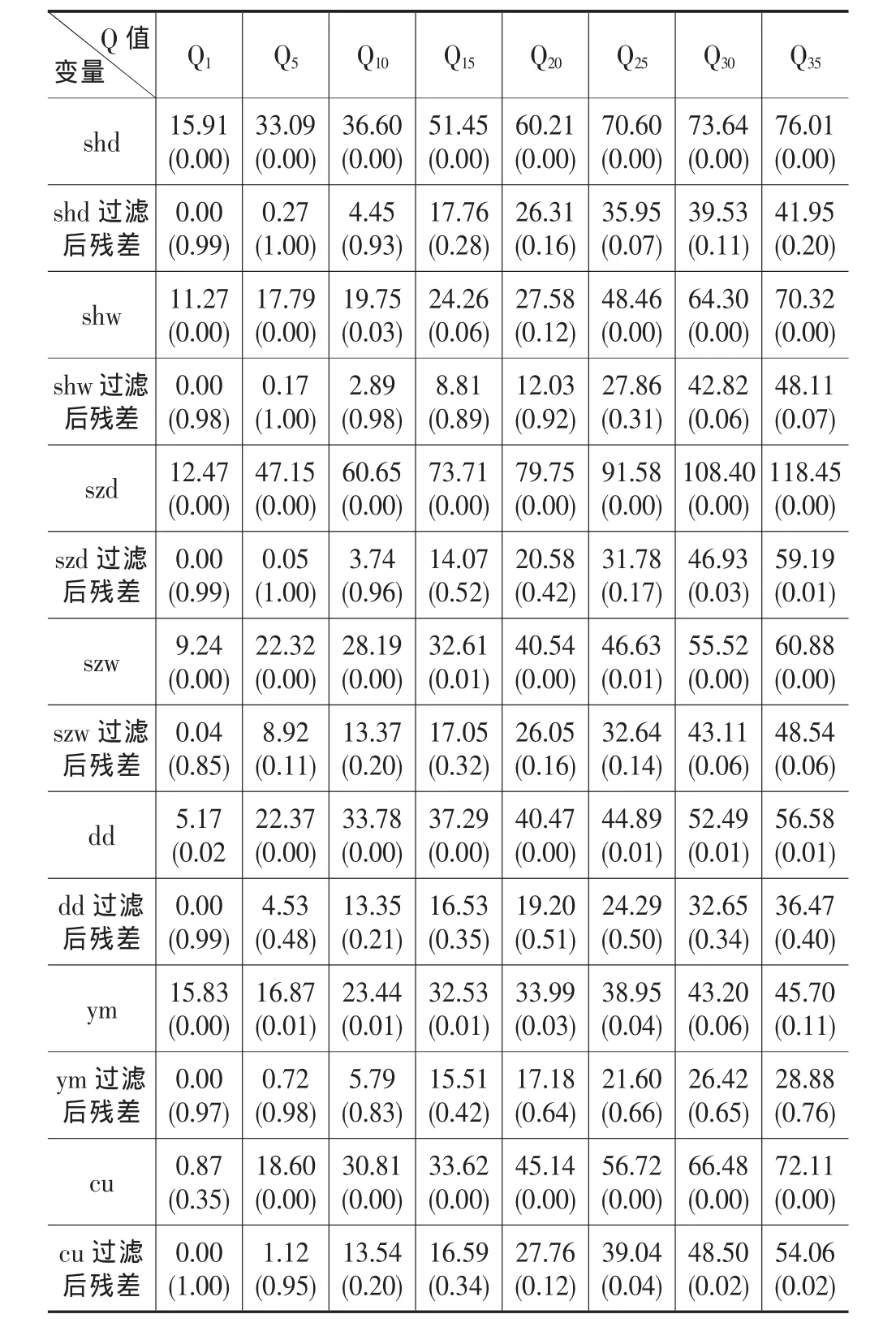
表4 证券收益率与线性过滤后残差线性相关性检验比较

对AR(p)模型过滤后的残差进行BDS检验，如表5的结果，在5%和1%的显著性水平下，检验临界值分别为1.96和2.25。所计算的统计值均远远大于临界值，因此所有检验均是显著的，说明该残差序列不是独立同分布的时间序列。同表1相比，线性过滤前与过滤后的BDS统计量相差不大，并且都是远远大于临界值，可以排除BDS检验显著拒绝i.i.d.是由证券收益率的线性依赖这一因素引起的，表明证券市场收益率序列的非线性结构是由混沌或者非线性随机过程引起的。

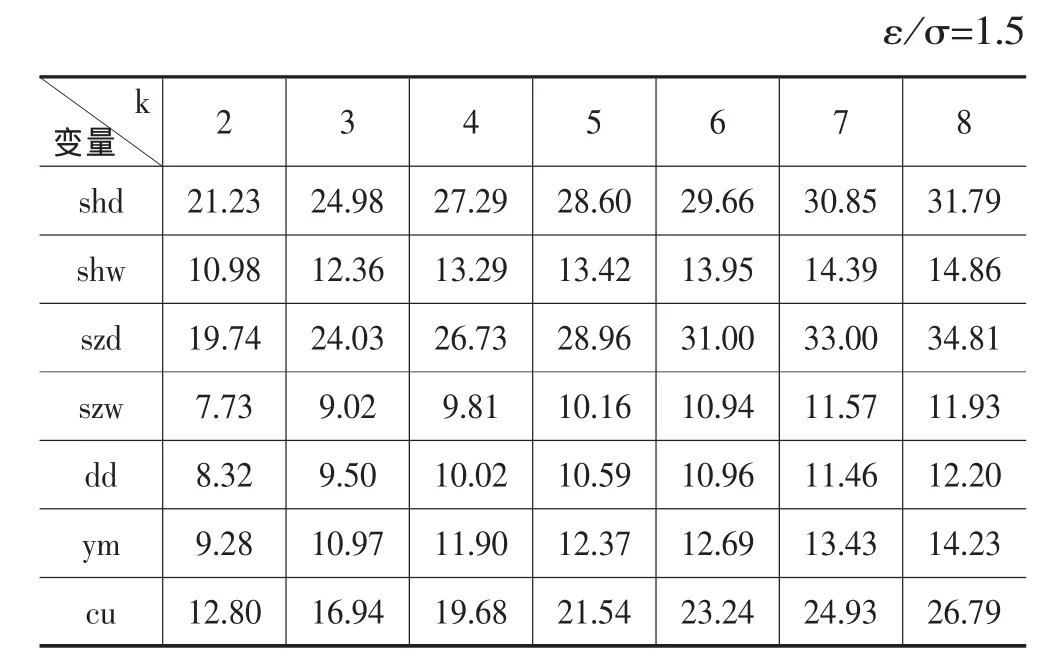
表5 证券收益率线性过滤后残差的BDS独立同分布检验

六、结论

用BDS统计检验方法，从统计上找到我国证券市场对数收益率序列存在非线性结构的证据，为混沌动力学行为的存在提供间接证据。通过稳定性分析和线性过滤后的BDS检验，排除了由非平稳和线性依赖产生非线性结构的可能。说明我国证券市场的非线性结构类型只能是混沌或非线性随机过程。这也就间接地提供了我国证券市场混沌存在的证据。

目前，能较好描述金融时间序列尖峰肥尾等非线性特征的主要有广义自回归条件异方差 （GARCH）模型、ARIMA模型和混沌三种非线性模型，其中ARCH和长期记忆模型都是随机模型，影响它们的因素很多，这些因素相互作用，造成复杂的价格行为；而混沌则不然，混沌是一种确定性的过程，这种过程是由几个变量所形成的简单函数所产生的[8]。这三种非线性模型哪种更能反映我国证券市场的非线性结构，这是本文进一步的研究方向。

［1］Scheinkman,J.,&B.LeBaron.Nonlinear dynamics and stock returns[J].Journal of Business,1989,62(3):311-338.

［2］Hsieh,David A.Chaos and nonlinear dynamics:application to financial markets[J].Journal of Finance,1991,46(5):1839-1877.

［3］王明进.一类期货数据的非线性数据特征分析[J].统计研究，2000，(7)：49-54.

［4］Brock W.,Dechert W.D.,Scheinkman J.A test for independence based on the correlation dimension[Z].Working paper,Department of Economics,University of Wisconsin,1986.

［5］Kanzler,Ludwig.Very fast and correctly sized estimation of the BDS statistic[Z].Working Paper,Christ Church and Department of Economics,University of Oxford,1999.

［6］Brock,William A.,David A.Hsieh,&Blake LeBaron.Nonlinear Dynamics,Chaos and Instability:Statistical Theory and Economic Evidence[M].Mass.:MIT Press,1993.

［7］罗奕,黄诒蓉.上海股市非线性结构的BDS检验[J].华北金融,2007,(6):7-9.

［8］赵华.混沌理论在经济中的应用研究[D].厦门：厦门大学.2005.

The Empirical Test for Nonlinear Structure of China's Stock Market

Zou Yi-zhong
（Wuyi University，Wuyishan Fujian 354300， China）

Through the BDS statistical test,the author discovered the evidence of the non-linear structure in the logarithmic return series of the China's stock market.And through stability analysis and the BDS statistical test after filtered linear,the author ruled out that the non-stationary and linear dependence are cause of the nonlinear structure.It is shows that the type of nonlinear structure in China's securities market only can be the chaos or nonlinear stochastic processes.

BDS statistical test； non-linear structure； the chaos

F830.91

A

1672-0547（2012）01-0033-04

2012-01-06

邹裔忠（1979－），男，福建泰宁人，武夷学院商学院讲师，硕士，研究方向：金融计量和物流金融。

福建省科技计划重点项目《武夷山生物多样性保护信息数据采集地方标准》（编号：2011Y0049）阶段性成果。