顺序更新式无序量测处理算法*
黄细凤,吴钦章
(1.中国科学院光电技术研究所,成都610209;2.中国科学院研究生院,北京100049)
在集中式融合目标跟踪系统中,所有传感器量测通过网络传输到融合中心,进行综合处理。处理中心和各传感器由各自的时统设备获得标准时间,各传感器对目标轨迹进行采样得到量测信息,并给每个量测加上一个“时戳”表示采样时刻。由于各传感器采样频率和量测预处理时间的不同,尤其是网络通信延迟的差异,使得多传感器量测传输到融合中心时,常会发生来自同一目标的较早的量测在较晚的量测之后到达的情况[1],即无序量测 OOSM(Out-Of-Sequence Measurement)现象。由于Kalman滤波算法只适于处理顺序量测ISM(In Sequence Measurement),因此基于Kalman滤波框架的量测融合算法不能直接处理状态估计的负时间更新问题,即用OOSM(量测时间为td)更新当前时刻tk(td<tk)的状态估计。
目前针对OOSM的滤波方法主要有4类:丢弃延迟量测法、重新滤波法、数据缓存法和直接更新法。丢弃延迟量测法采用丢弃OOSM的策略,它会造成大量信息丢失,导致目标跟踪精度下降甚至丢失目标。重新滤波法要求滤波器存储过去一段时间的量测数据和部分中间结果,从产生OOSM的时刻起重新滤波,它能得到与有序量测顺序处理时相同的结果,但其所需存储量和计算量会随传感器数目、目标数目及延迟时间的增长而显著增加。数据缓存法把过去一段时间的量测缓存起来,按探测时间排序,然后进行滤波,它也可以获得与有序量测顺序处理时相同的结果,但是需要较大的存储空间而且输出严重滞后。直接更新法[2-10]既不丢弃 OOSM,又不缓存历史数据,而是直接使用OOSM更新当前时刻的状态估计,使其能达到或逼近将量测顺序处理时的滤波精度。由于直接更新法存储量和计算量小,滤波输出没有滞后,又有高精度的滤波性能,因此是国内外学者的研究重点。
对于单个OOSM的一步延迟问题,Bar-Shalom提出了A1算法[2],同时命名Hilton等提出的次优算法为 B1算法[3]。周文辉等[4]指出:A1算法仅在过程噪声连续离散化模型下最优,同时提出一种与过程噪声离散化模型无关的最优OOSM滤波算法。对于单个OOSM的多步延迟问题,Mallick M等[5]提出了Bl算法,Bar-Shalom等[6]提出了 Al1和Bl1算法,用量测等效法将多步延迟问题等效为单步延迟问题,再使用A1和B1算法进行处理。在预先知道最大延迟的前提下,Zhang K S和Li X Rong提出了全局最优的 Zl算法[7-8]。随后又有多种方法被提出[9-13]处理单个 OOSM 的一步和多步延迟问题。对于多 OOSM 问题,目前研究成果还较少[1,14-16]
本文对于解决单个OOSM问题借用重新滤波法的思想,提出了一种基于等价量测的顺序更新式算法来处理单OOSM的多延迟问题。
1OOSM问题描述
假定对一目标进行跟踪,相应的运动方程和量测方程为:
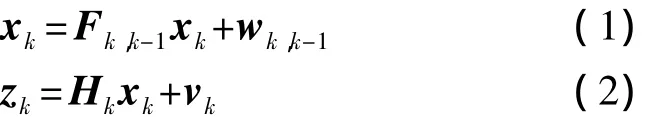
假定在tk时刻,已有状态估计
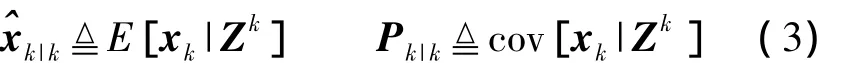

在式(3)的状态估计已经计算出来以后到达处理中心。然后要用较早的量测式(4)来更新tk时刻的估计,即计算

一般来说,量测时刻 td可能 l步延迟,即为最大滞后步数。当 l=1时,为一步滞后 OOSM,当 l>1时,即为多步滞后OOSM。解决多步滞后OOSM问题时,为了减小存储量和计算量,一般采用一步解算法处理[6-13]。
2 基于等价量测的顺序更新式算法
基于等价量测的顺序更新算法的基本思想是:当接收到滞后到达的量测即无序量测时,将滤波过程返回至该无序量测的探测时刻,重新滤波;但是在重新滤波时,探测时刻晚于该无序量测的所有量测用一个等价量测来代替,而不存储这段时间的量测数据和中间结果。因此,关键步骤是求这个等价量测。
2.1 等价量测
等价量测的概念在解决l>1步延迟的OOSM问题上应用普遍,Bar-Shalom Y教授等人在A1,B1算法的基础上提出的Al1,Bl1算法[6]就是基于等价量测进行的。
首先定义tk时刻的等价量测

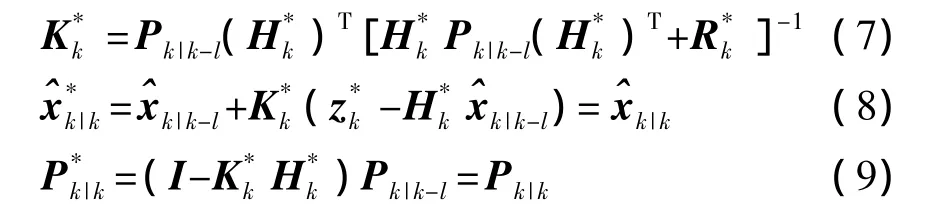

由式(9)、式(10),我们得到等价量测的滤波增益为
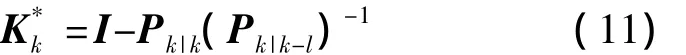
由式(8)、式(10),我们得到等价量测为
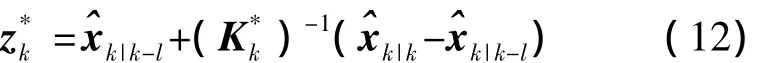
由式(7)、式(10)、式(11),我们得到等价量测噪声协方差阵
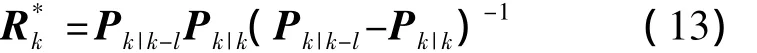
式(7)~式(13)中
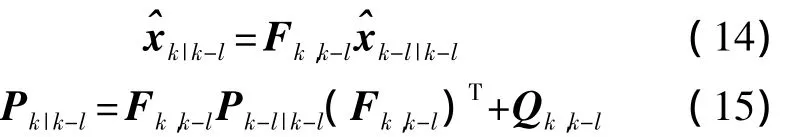
在式(10)的条件下,我们求得了等价量测,如果实际观测矩阵为,则实际的等价量测,实际的等价量测噪声协方差阵。
2.2 顺序更新
用zd进行更新,有:
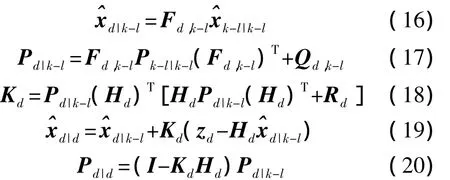
其中,有
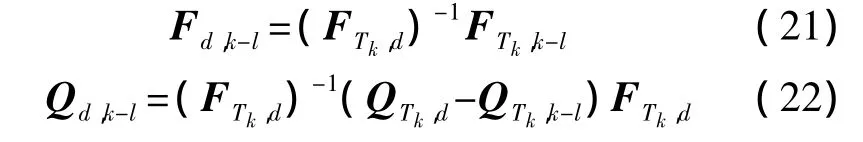
表征该量测噪声与其他各量测噪声之间的相关性。下标中的Tk表示该融合周期的融合时刻,且Tk≥tk。
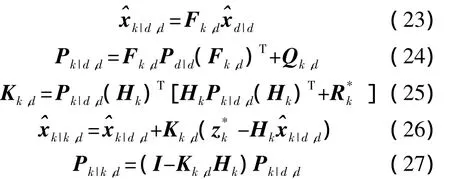
其中有:

3 算法分析
3.1 数据存储量
本文算法可处理多步延迟OOSM问题,所以与数据存储量较小的Al1,Bl1算法来比较。对于l步OOSM问题,在未收到OOSM之前,l未知,为讨论方便,假定最大延迟步数s是固定的。新算法需要存储:,n 个标量,③个标量,n为目标状态向量的维数,因而所需额外存储量为[(n2+3n+2)s]/2。由文献[6]知,Al1和Bl1算法额外存储量分别为[(n2+3n+2)s]/2 和[(n2+n+2)s]/2,因此本文算法的额外存储量与Al1算法相当。
3.2 最优性分析
4 仿真分析
假定有5个传感器对同一目标进行跟踪,各传感器的量测,测得噪声为零均值的高斯白噪声,方差分别为5、10、15、20、25。该目标沿 x 轴做匀加速运动,目标运动方程和量测方程分别为式(1)和式(2)。
式(1)中目标状态向量为

目标状态转移矩阵为

累积过程噪声的协方差为
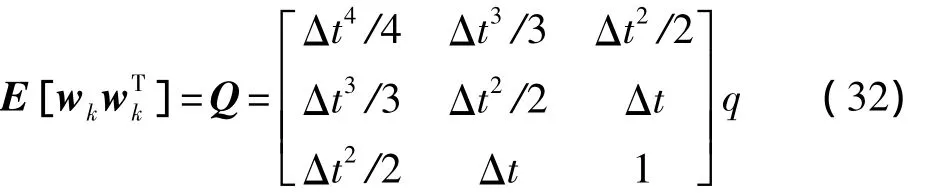
其中,Δt为探测时间间隔;q为连续时间过程噪声的功率谱密度,q=1 m2/s2。
式(2)中目标量测矩阵为

量测噪声的协方差为

4.1 仿真1
设在t0=50 s时,已获得状态估计和协方差,在Toosm=[t0,t1],t1=51 s的时间间隔内,接收到的传感器2的量测是无序量测,它的探测时刻为50.3 s。假定对应于延迟步数l=1,2,3,在Toosm内相应的各传感器探测时刻如表1所示。
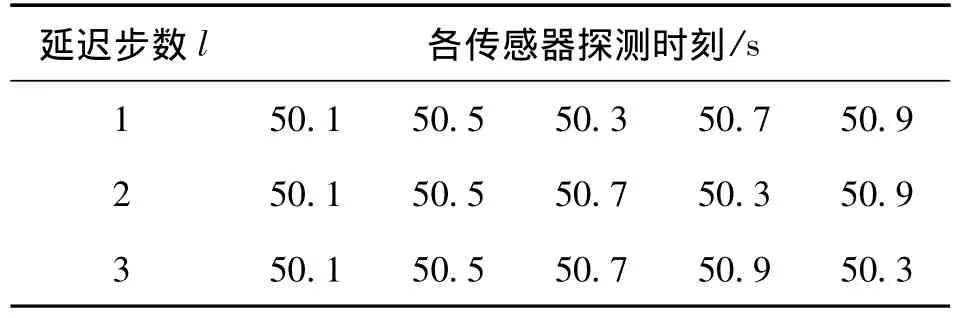
表1 仿真1 Toosm内相应的各传感器探测时刻
我们对本文的算法,Al1算法以及数据缓存法,在延迟步数l=1,2,3的OOSM情形下进行处理,将所得的用无序量测进行更新后的最新时刻的协方差矩阵的迹和位置均方根误差做出比较,比较结果显示在表2中,表中的数据是通过100次的Monte Carlo仿真得到的平均值。表中括号内求的是相对数据缓存法的结果的偏差,偏差越小,效果越好。
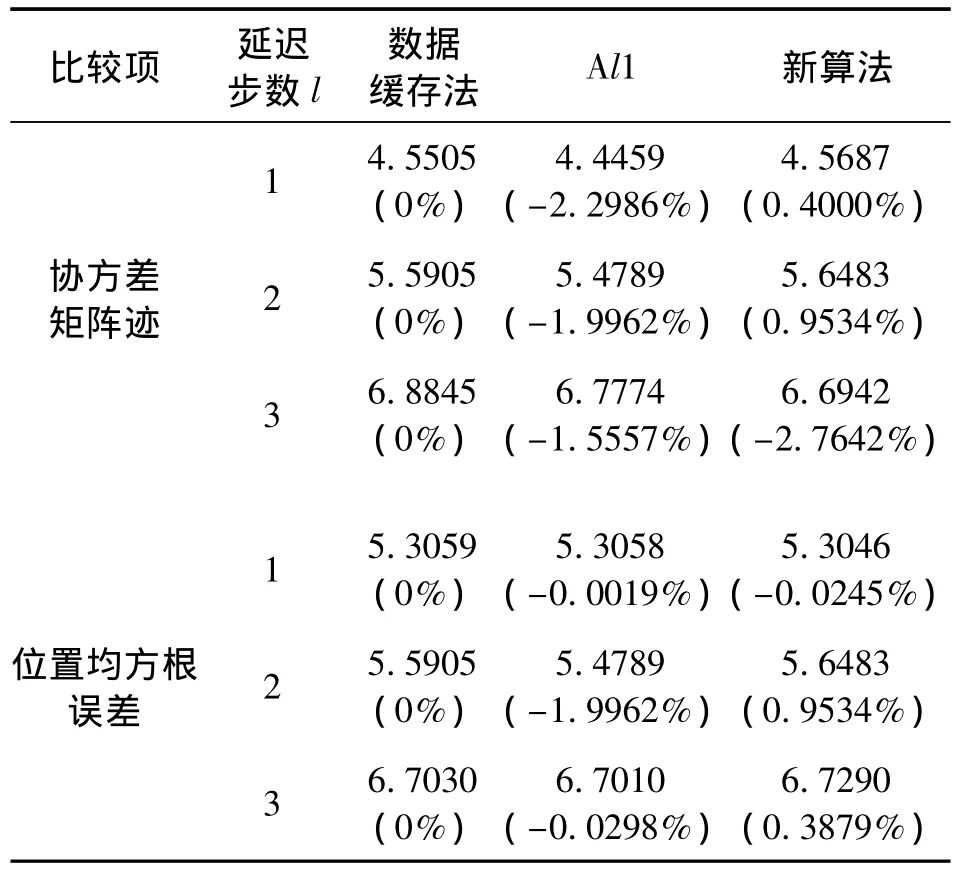
表2 仿真1的各算法的结果比较
4.2 仿真2
假设处理中心每个融合周期内接收到的传感器2的量测数据都是无序量测,对应于延迟步数l=1,3,参照表1。同样用本文的算法,Al1算法以及数据缓存法进行处理,将所得的用无序量测进行更新后的最新时刻的协方差矩阵的迹和位置均方根误差做出比较,比较结果如图1,图中的数据是通过100次的Monte Carlo仿真得到的平均值。

图1 仿真二的各算法的结果比较
4.3 结果分析
由于仿真中设置了算法的模型与目标的运动较匹配,因此过程噪声的影响较小,从仿真结果中可以看出:OOSM 延迟时间较短(Δt=0.2 s,0.4 s,0.6 s)时,能满足该算法的最优性条件。从误差协方差矩阵的迹的比较可知,新算法的误差协方差矩阵的迹的偏差略大于Al1和数据缓存法,且随延迟步数增加而偏差略有增加,这是由于求解等价量测时忽略过程噪声相关性所引起的;同时从表2中也可以看到,随着延迟步数增加,以最优的数据缓存法作为基准,性能下降是非常小的,有时甚至并不一定会下降。从位置均方根误差的比较可知,新算法与数据缓存法和Al1算法有着相同的滤波精度。
5 结论
本文针对无序量测处理问题,结合等价量测与重新滤波法,提出了一种基于等价量测的顺序更新式处理算法。该算法用等价量测代替重新滤波法中需要缓存的量测序列和中间结果,然后从无序量测处开始用无序量测和等价量测进行顺序式的更新。该算法有较小的额外存储量;对于一步延迟来说是最优的,对于多步延迟来说,当过程噪声很小且无序量测延迟时间较短时,接近最优且性能下降非常小。本文算法处理的只是单个OOSM的情况,对于多OOSM问题还有待进一步研究。
[1] 韩崇昭,朱洪艳,段战胜,等.多源信息融合(第二版)[M].北京:清华大学出版社,2010.
[2] Bar-Shalom Y.Update with Out-of-Sequence Measurements in Tracking:Exact Solution[J].IEEE Transactions on Aerospace E-lectronic Systems,2002,38(3):769-778.
[3] Hilton R D,Martin D A,Blair W D.Tracking with Time Delayed Data in Multi-Sensor Systems[R].Technical Report NSWCDD/TR-93/351,AD-A355269,Dahlgren,VA,August 1993.
[4] 周文辉,李琳,陈国海,等.单步延迟无序量测滤波算法的最优性分析[J].中国科学 E 辑:信息科学,2007,37(4):564-580.
[5] Mallick M,Coraluppi S,Carth el C.Advances in Asynchronous and Decentralized Estimation[C]//Proc.of the IE EE Aerospace Conference,2001,4:1873-1888.
[6] Bar-Shalom Y,Chen H M,Mallick M.One-Step Solution for the Multi-Step out of Sequence Measurement Problem in Tracking[J].IEEE Transactions on Aerospace Electronic Systems,2004,40(1):27-37.
[7] Zhang K S,Li X R,Zhu Y M.Optimal Update with Out-of-Sequence Measurements for Distributed Filtering[C]//Proceedings of the Fifth International Conference on Information Fusion,Annapolis,MD,2002,7:1519-1526.
[8] Zhang K S,Li X Rong,Chen H,et al.Multi-Sensor Multi-Target Tracking with Out-of-Sequence Measurements[C]//Proc.Of the 6th International Conference on Information Fusion.USA:IEEE.2003.:672-679.
[9] Yu Anxi,Liang Dian nong,Hu Weidong,et al.A Unified Out-of-Sequence Measurements Filter[C]//IEEE International Radar Conference,2005:453-458.
[10]高蕊,秦超英,张希彬.无序量测的状态更新估计算法[J].传感器技术学报,2006,19(2):501-503.
[11]何雅晶,徐毓.单个非顺序量测的异步航迹融合算法[J].火力指挥控制,2007,32(7):47-50.
[12]王炜,黄心汉,徐忠昌,等.一种新的无序量测处理算法[J].电子与信息学报,2009,31(8):1996-2000.
[13]王炜,黄心汉,王公宝.一种最佳多延迟无序量测处理算法[J].系统工程与电子技术,2009,31(11):2592-2596.
[14]高蕊,秦超英,张希彬.无序量测的状态更新估计算法[J].传感技术学报,2006,19(2):501-503.
[15] Xiaojing Shen,Zhu Yunmin,Song Enbin.Optimal Centralized Update with Mutiple Local Out-of-Sequence-Measurements[J].IEEE Transaction on Signal Processing,2009,57(4):1551-1562.
[16] Xiaojing Shen,Yunmin Zhu,Enbin Song.Globally Optimal Distributed Kalman Fusion with Local Out-of-Sequence-Measurements Updates[J].IEEE Transaction on Automatic Control,2009,54(8):1928-1934.
[17]葛泉波,文成林.基于状态转换的顺序式异步数据融合算法[J].系统工程与电子技术,2008,30(12):2322-2328.

