水下传感器网络移动节点定位问题研究*

胡 钢 ，张 瑞，刘宴佳

(1.河海大学计算机与信息学院(常州)，江苏 常州 213022；2.常州市传感网与环境感知重点实验室，江苏常州 213022)

无线传感器网络(WSN)是信息科学领域中一个全新发展方向，它融合了微处理器、智能传感器与通信技术，使得传感器节点成为集感知信息、交换信息、协调控制等功能于一体的有机结合体，被认为是下一代互联网的重要组成部分。根据应用环境的不同，无线传感器网络又可分为地面传感网、地下传感网以及水下传感网。近年来，随着各国政府对海洋开发的重视，水下传感网进步飞速，现在它已经广泛应用于海洋数据采集、污染检测、海上探测、灾难预警、救援打捞和军事监测等方面［1］。

在大多数应用中，如何快速有效地对目标节点的物理位置进行定位，是国内外许多研究机构和学者所共同探讨的问题［2］。在水下救援打捞等领域，则需要对移动的目标节点进行定位，对定位精度也提出了更高的要求，这就给水下传感网的定位算法设计带来了挑战。目前，针对水下传感网移动节点定位的研究并不多，本文首先分析了现有的定位算法及在水下定位中的优劣，然后针对水下传感网的特性，提出了一种基于Chan算法改进的M-Chan算法，它通过曲线拟合进行运动轨迹预测，利用节点移动特性修正估计位置，从而使节点定位达到较高的精度，并进行了仿真与误差分析。

1 相关算法分析

常见的节点定位算法，根据定位过程中是否需要测量节点间的距离，分为基于测距的算法和无需测距的算法两类。无需测距的算法主要通过节点之间的连通性实现节点定位；基于测距的算法依赖额外硬件测量节点间的距离信息，如接收信号强度(RSSI)、信号的到达时间(TOA)、不同信号的到达时间差(TDOA)以及信号的到达角度(AOA)。该类算法需要额外器件，增加了节点成本和功耗，但与无需测距的算法相比，定位精度更高［3］。而在水下环境中，温度、障碍物、传播模式等条件都是不断变化的，现有的传播衰减模型又不精确，故测量接收信号强度(RSSI)存在困难，精度受限［4］。基于到达时间差(TDOA)的算法不需要复杂的测距设备，定位精度较高，在水下传感网定位中最为适用。

水下传感器网络主要依赖声波进行通信，声波的传播速率比电磁波小几个数量级，通信过程中的传播延迟较大。如果目标节点移动速度很快，那么在定位信号从目标节点到锚节点的传播时间内，目标节点的位移较大，从而使定位精度下降。目前学术界提出的一些动态定位算法，如 DLS算法［5］、MSPF 算法［6］、MCL 算法［7］以及基于 MCL 的几种改进算法:如MCB算法［8］，解决了MCL方法采样效率低的问题；Dual-MCL、Mixture-MCL 算法［9］对预测和滤波阶段进行了改进等，这些算法并没有一项是特别针对水下传感网中锚节点多为静止状态的情形设计的，也没有考虑到水下传感网的传输特性，而且它们多不基于测距，定位精度普遍不高。

2 Chan算法原理

常见的 TDOA定位算法包括 Chan算法［10］、Fang算法［11］、Taylor级数展开算法［12］等。Chan 算法是一种求解双曲线方程组的非递归算法，算法首先用加权最小二乘法(WLS)得到一初始解，再用得到的估计位置坐标及附加变量等约束条件进行二次WLS估计，最后得到改进的位置估计。该算法计算量小，并且经仿真表明，Chan算法具有更精确的代数解。

图1 移动节点定位示意图

令未知矢量Za=［1］T，其中 Zp=［x y］T，有TDOA噪声的误差矢量:

其中

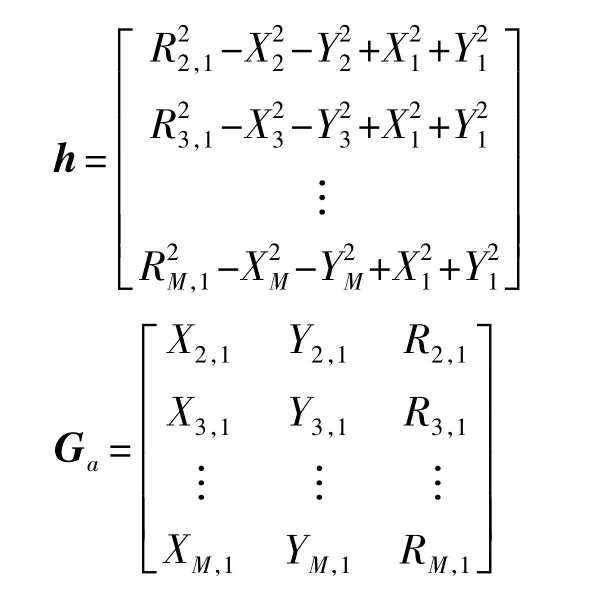
式中(xy)为移动目标的待估计位置，(Xi Yi)为第i个锚节点的已知位置，Ri，1为第i个锚节点相对于第一个锚节点的距离差，则将测得的Ri，1代入，经过一次WLS求解该方程得:

将Za的元素表示为:

其中e1，e2，e3为Z的估计误差，Z的前两个元素减去X1，Y1，再对各元素求平方可得Za的误差矢量:

其中

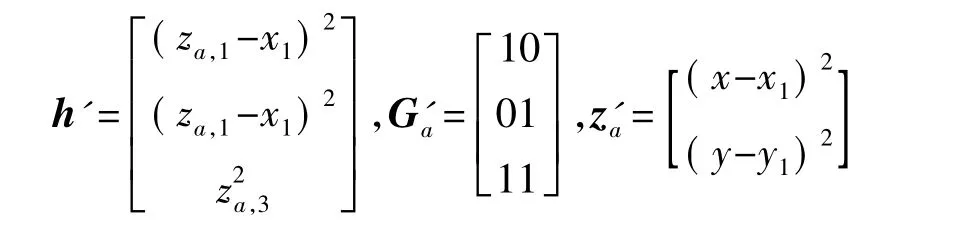
可得Z'a的ML估计为:

最终移动目标的定位估计位置为:

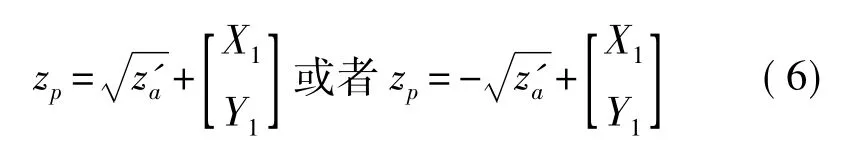
Chan算法的性能主要受非视距传播NLOS的影响，水下信道可认为是视距信道，因此Chan算法较适用于水下传感网的定位应用。但由于它是针对静态网络提出的算法，没有考虑到节点的移动性；当节点运动速度较快时，水下较高的信号传播延迟将会带来不小的定位误差。

3 改进的M-Chan算法

曲线拟合是用连续曲线逼近平面上离散坐标之间函数关系的一种数据处理方法。实际计算中通过观测得到一系列坐标Si(xi，yi)(i=1，2，3，…，n)，用相应的解析表达式y=f(xi)来反映坐标变量之间的依赖关系，就可以在一定意义下最佳逼近已知数据，反映其变化趋势。其中f(xi)常称作拟合函数，当f(xi)为多项式时又称多项式拟合，求解f(xi)时应满足:

式(7)称为曲线拟合的最小二乘条件，由多元函数求极值的必要条件，得

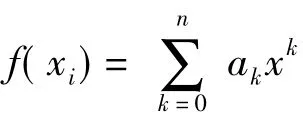
水下传感网进行TDOA定位时，锚节点可随机布置在水面某区域，配有GPS设备以确定自己的位置坐标，目标节点在水下运动并周期性地向锚节点发送定位信号。锚节点通过全向换能器接收水下节点的信号并计算到达时间差，锚节点之间需要时间同步，而目标节点只需保证自己的时钟稳定。在定位过程中，目标节点是移动的，假设其运动方向不确定，但是知道在当前时刻的运动速度Vi，如果mi是待定位节点在当前时刻的估计位置，那么该节点在经过Δt时刻后的可能位置就近似在以mi为圆心、VΔt为半径的圆上。本文提出的M-Chan算法正是利用节点的这种移动特性和曲线拟合方法对传统的Chan算法进行了改进，算法的基本流程如下:

(1)初始化阶段

本算法假设目标节点在水下某二维平面上随机运动(三维情况可由二维拓展坐标系得到，由于原理相同，故本文不再推导)，锚节点随机布置在水面上的某区域内，目标节点周期性地发送定位信号，假定周期为T，称每次发送信号的时刻为采样时刻。当目标节点进入锚节点定位区域时，首先节点根据传统Chan算法估计自己前3个采样时刻的位置坐标mi=(xi，yi)(i=1，2，3)，并存放在一个拟合数据队列S=(m1，m2，m3)中，然后对拟合队列中的坐标数据进行多项式拟合，计算出该节点运动轨迹的曲线参数，从而预测出移动节点的初始运动曲线fn(xi)。虽然前3个时刻的定位没有考虑声波的传播时延，但它们拟合出的节点运动曲线是可信的。

(2)定位阶段

从第3个采样时刻起，利用节点的移动性对估计位置进行修正。Chan算法得到的估计位置没有考虑声波从目标节点到锚节点的传播延迟Δt，那么节点的实际坐标应是在此基础上位移Δt时间后的新位置。系统发起定位计算的时刻为收集到足够的TDOA测量值时，此时的Δt等于声波从目标节点传播到其通信半径内最远的锚节点所用时间，为简化计算，用通信半径代替这个距离，从图2中可以看出，当锚节点密度较大时，目标节点到最远可定位锚节点的距离无限接近于通信半径。那么此时传播延迟Δt=R/c，其中R为通信半径，c为声波在水下的传播速度。

图2 不同密度下最远可定位锚节点距离示意图

假设前三次采样时刻分别为t1，t2，t3，函数h(ti)为ti上的函数值，那么根据牛顿插值多项式，可以利用前3个时刻的xi=h(ti)来预测t时刻的，公式如下:

其中

由式(9)可以求得目标节点在t3时刻x轴方向上的速度为

同理可求得y轴方向上的速度vy，可知目标节点在t3时刻的运动速度为

此时由于运动的连续性，以t3时刻的Chan算法估计坐标为圆心，v*Δt为半径作圆，将此圆方程与拟合曲线函数f(xi)联立，得方程组

求解方程组(15)，取其根中与上一时刻估计位置欧氏距离较远的一个作为t3时刻的估计位置，并将其写入拟合队列，替换掉原有的t3时刻估计坐标。如果所求方程组无解，则定位失败，直接采用Chan算法估计坐标作为节点的最终估计位置。

(3)拟合阶段

当移动节点在新的采样时刻产生定位信号时，通过Chan算法首先计算出该时刻的一个初始位置，将其添加到拟合队列的末尾，如果队列长度超过3，则丢弃队列第1项，以保证队列中保存的节点位置坐标是不断更新的。此时对拟合队列进行多项式拟合，即可得到节点当前预测运动曲线f(x)。然后重复定位阶段，计算出当前时刻的估计坐标，并将其写入拟合队列替换掉原当前时刻的估计位置。对于多项式曲线的拟合，要提高拟合精度和效果，就需要提高曲线阶数，而阶次太高又带来计算上的复杂性及其他方面的不利，故在实际应用中一般取不超过6的整数值［14］。

4 仿真分析

本文为了检验M-Chan算法的性能，用Matlab对M-Chan算法与传统Chan算法进行了仿真对比分析。仿真中，为了使结果更加接近真实，在边长L=1000 m的正方形区域内随机布置M=200个锚节点，锚节点的部署服从均匀分布。另布设一单目标节点，所有节点的通信半径R=200 m，声速取c=1 200 m/s，目标节点采用随机Waypoint移动模型，平均移动速度va=15 m/s，且认为节点在二维平面上运动。假定算法中锚节点之间是时间同步的，TDOA的测量误差的分布服从均值为0，方差为σ2=1的高斯分布［15］，图3即为一次仿真的定位结果示意图。

图3 移动节点定位仿真示意图

文中的平均定位误差为节点所有定位时刻的定位误差取均值，采用节点的估计位置和实际位置之间的欧氏距离来表示，拟合数据队列的长度为3，拟合多项式的阶数k=2。所有的仿真结果均为通过对20次独立仿真结果取均值获得。下面从几个方面分析该定位算法的定位性能:

(1)节点移动速度:

图4是节点移动速度对平均定位误差的影响。仿真结果显示，随着移动速度的增加，Chan算法的定位精度逐渐降低，因为节点速度增大使目标节点在定位信号的传播过程中移动更远的位置，从而使误差相应增大；而M-Chan算法则基本不受节点移动速度的影响，定位误差较为稳定，节点速度快时，性能较原算法有较大提高，当节点平均移动速度为27 m/s时，精度可提高8.87%。

图4 节点平均移动速度与定位误差

(2)通信半径

图5是随通信半径的变化，平均定位误差的变化曲线图。通常意义上，节点通信半径的增大可以使采样时刻接收到定位信号的锚节点数量增多，从而增加双曲线方程组的方程个数，使定位精度提高。但在实际仿真中，平均定位误差在通信半径增大时逐渐增高，表明定位性能不升反降。经分析仿真过程认为，造成这种现象的原因是当目标节点在锚节点区域外运动时，由于通信半径的增加，能够接收到定位信息的锚节点数量也随之增加，这就使得之前不能被定位的点变为可定位点，如图3中虚线框所示的定位点。这些点能够利用的锚节点有限，定位误差较大，所以总体定位误差随之增高。但误差大总要优于不能定位的结果，因此综合来看，总体定位性能还是随通信半径增大而提高的。对M-Chan算法来说，通信半径的增大意味着其不再近似等于目标节点距最远可定位锚节点的距离，这增加了计算信号传播时延的误差，使总体误差增大。节点通信半径为550m时，较原算法约提高精度8.59%。

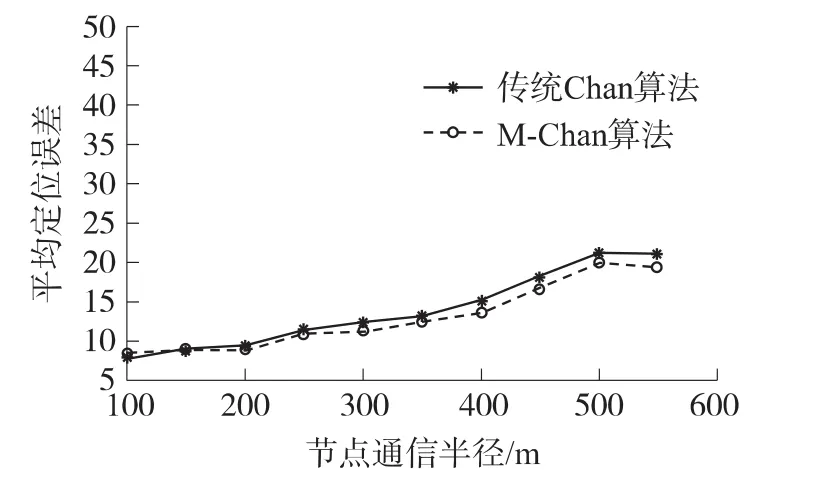
图5 节点通信半径与定位误差

(3)锚节点密度

仿真中的锚节点密度通过1 000 m×1 000 m区域内的锚节点个数来表示，从图6可以看出，增加锚节点密度可以有效提高定位精度，当锚节点密度达到某一阈值后，两种算法的平均定位误差均趋于稳定。这是因为仿真中，考虑到计算复杂度，Chan算法只取最多7个锚节点进行定位计算，锚节点密度达到一定程度时，每定位时刻可定位锚节点数量饱和，故定位误差趋于一稳定值。M-Chan算法在锚节点密度较大时性能较原算法有所提升，在每106m2布置450个锚节点的情况下，精度可提高8.01%。

图6 锚节点密度与定位误差

5 总结

本文针对水下传感网中研究较少的移动节点定位，提出了一种改进M-Chan算法。该算法通过曲线拟合进行运动轨迹预测，利用节点移动特性修正估计位置，从而提高了移动节点的定位精度。最后对照传统Chan定位算法，从节点移动速度、通信半径、锚节点密度等不同方面进行了仿真比较，对比了两种算法的平均定位误差。仿真结果表明，M-Chan算法的定位性能提高约5% ～10%，尤其当节点高速移动时，M-Chan算法明显优于传统Chan算法。

［1］Akyitdiz I F，Pompiti D，Melodia T.Underwater Acoustic Sensor Networks:Research Challenges［J］.Ad Hoc Networks(Elsevier)，2005，3(3):257－279.

［2］江冰，吴元忠，谢冬梅.无线传感器网络节点自定位算法的研究［J］.传感技术学报，2007，6(20):1381－1385.

［3］张正勇，梅顺良.无线传感器网络节点自定位技术［J］.计算机工程，2007，33(17):4－6.

［4］孙利民，李建中，陈渝，等.无线传感器网络［M］.北京:清华大学出版社，2005.

［5］Chen Xun，Han Peng.A Viable Localization Scheme for Dynamic Wireless Sensor Networks［C］//Computer and Computational Sciences，First Interactional Multi-Symposiums.Volume 2，Apri 2006:587－593.

［6］罗海勇，李锦涛，赵方.基于均值漂移和联合粒子滤波的移动节点定位算法［J］.传感技术学报，2009，3(22):378－386.

［7］Hu L，Evans D.Localization for Mobile Sensor Networks［C］//Proceedings of the 10th Annual International Conference on Mobile Computing and Networking，2004:45－47.

［8］Aline Baggio，Koen Langendoen.Monte Carlo Localization for Mobile Wireless Sensor Networks［J］.Lecture Notes in Computer Science，2006，4325(11):317－328.

［9］Baggio A，Langendoen K.Monte Carlo Localization for Wireless Sensor Networks［C］//Proc of the 2nd Int’l Confon Mobile Ad-Hoc and Sensor Networks(MSN 2006).Hong Kong:Springer Verlag Press，2006:317－328.

［10］ChanY T，Ho K C.A Simple and Efficient Estimator for Hyperbolic Location［J］.IEEE Transactions on Signal Processing，1994，42(8):1905－1915.

［11］Fang B T.Simple Solutions for Hyperbolic and Related Position Fixes［J］.IEEE Trans.on Aerosp.Electron.Syst，1990，26:748－753.

［12］Foy W.Position-Location Solutions by Taylor Series Estimation［J］.IEEE Trans.Aerosp.Electron.Syst，1976，AES－12(2):187－193.

［13］黄梅根，常新峰.一种基于蒙特卡罗法的无线传感器网络移动节点定位算法研究［J］.传感技术学报，2010，4(23):562－566.

［14］焦竹青，熊伟丽，张林，等.基于曲线拟合的无线传感器网络目标定位算法［J］.东南大学学报(自然科学版)，2008，91(38):249－252.

［15］Li Cong，Zhuang Wei-hua.Non-Line-of-Sight Error Mitigation in TDOA mobile location［C］//IEEE Global Telecommunications Conference，San Antonio TX USA，Nov 2001:680－684.