电容耦合电阻层析成像传感器结构优化设计研究*

王保良，张伟波，黄志尧，冀海峰，李海青

(浙江大学控制科学与工程学系工业控制技术国家重点实验室，杭州 310027)

电阻层析成像ERT(Electrical Resistance Tomography)作为一种重要的过程层析成像技术，是20世纪80年代中后期发展起来的一种成像技术［1］。在冶金、石油、食品、能源等领域的两相流测量中具有广泛的应用前景。与其它成像技术相比，如X射线、γ射线、超声等，ERT成像技术具有成本低，响应速度快，安全性好等优点［2］。但传统的ERT传感器电极安装时需要穿透管壁并与被测液体直接接触，因此有可能会降低管道耐压强度，同时引起电极腐蚀等问题。

20世纪80年代，分析化学领域有学者提出一种电容耦合非接触电导探测技术［3－5］，用于测量微米级通道内液体的电导率。该技术自提出之后就引起很多学者的关注，并得到了较深入的研究和改进［6－8］，但在多相流常规管道应用领域却鲜有文献报道。

基于此原理，本研究小组提出一种非接触式电容耦合电阻成像技术CCERT(Capacitively Coupled E-lectrical Resistance Tomography)［9］。该系统的传感器电极直接安装在管道外壁，不与管道内液体接触，结构与电容层析成像ECT(Electrical Capacitance Tomography)传感器类似［10］，如图1(a)所示。通过对每组电极对上施加交流电压，从而形成交流通路，就可以获得各电流通路上的串联耦合电容及电阻，而电阻即反映电极对所在电流通路上的管道内部溶液的电导信息，进而通过一定的图像重建算法获得电极所在管道截面的实时电导分布图像。基于电容耦合原理的电阻层析成像系统的可行性已得到了初步的实验验证［9］。

图1 CCERT传感器结构示意图

虽然新提出的CCERT传感器结构与传统ECT类似，但内部传感机理与ECT不同。同样，尽管管道内部液体的电导均为CCERT与传统ERT传感器的检测对象，然而二者的传感器结构又有很大的区别。因此，以往的ECT与ERT的设计经验虽然可提供一定的借鉴与参考［11－15］，但必须针对 CCERT 这种新的传感器重新进行建模和优化设计研究，从而提高系统稳定性及检测精度等。本文主要针对CCERT传感器屏蔽罩及径向电极对传感器性能影响进行分析研究，从而为传感器设计提供指导。

1 CCERT系统组成及数学模型

1.1 CCERT系统组成及测量原理

CCERT系统主要由电极阵列传感器、数据采集系统和成像系统3部分组成。电极阵列等间隔围绕被测管道安装一周，如图1所示。数据采集系统从传感器电极阵列采集反映内部电导分布的数据，在上位机利用一定的图像重建算法进行图像重建及显示，从而获得管道内部截面电导分布的实时图像。

每次测量中，任意两个电极分别作为激励和检测电极，其中激励电极接交流电压源，检测电极接地，如图1(b)所示，图中电极1为激励电极，电极7为检测电极，从而在管道内部建立起敏感场。激励检测电极间等效电路如图2所示，其中R表示电流所在通路上管道内部液体的等效电阻值，C1和C2分别表示电极、管壁及导电液体表面形成的两个耦合电容。通过采集检测电极上的交流电流值，经过计算就可获取相应电流路径上的等效电容及电阻值。当任意两个电极(激励和检测电极对)间的测量结束后，就完成一个测量周期。对于N电极传感器，每个测量周期共有N(N－1)/2组独立测量值。本文以12电极传感器为研究对象，因此共有66组独立测量值。最后在上位机通过一定的图像重建算法，利用这66个电阻值重建内部液体电导分布的实时图像。

图2 激励检测电极对间的等效电路

1.2 传感器场域数学模型

为了对CCERT正问题进行深入研究，建立其场域数学模型是研究问题的基础。由于数据采集系统的激励频率暂定为100 kHz，而管道直径为0.11 m，远小于电磁波的1/6波长，满足第3类似稳场条件，因此CCERT传感器敏感场域可用准静态电磁场分析。同时基于实际的传感器结构及数据采集系统工作模式，传感器场域描述为:

其中 σ(x，y)，ε(x，y)，φ(x，y)分别表示管道内部场域电导率，介电常数以及电势分布。Г1，Г2，…，Г12表示电极在管道上的空间位置，Ω表示传感器场域，n表示管壁单位法向量。由此可得，各电极边界条件分别为:激励电极接交流电压源、检测电极接地、其它电极悬空。

1.3 灵敏场

首先对正问题进行研究，建立了场域的2D有限元模型，为进一步计算模型的灵敏场及后续的图像重建提供基础。

电阻灵敏度定义为［16］:

式中:δRi，j定义为检测电极对i，j之间的电阻值变化量，δσ指某个单元的电导率变化量，ΔA指相应单元的面积。

对于N电极CCERT传感器，由于电极空间位置的对称性，典型的灵敏场共有N/2组，对于本研究采用12电极模型，共有六组典型的电阻灵敏场，以电极1 为激励电极，分别是 1－2、1－3、…、1－7 电极对。其它灵敏场可通过对此六组典型灵敏场进行一定旋转变换获得。六组电阻灵敏场如图3所示。

图3 6组典型电极对间电阻灵敏度

由图3可以看出，电阻灵敏度在传感器场域分布不均匀，随着离散相的位置不同而变化。激励电极和检测电极附近的灵敏度最大，场域中心灵敏度最低，这与典型的ECT传感器灵敏场类似［10］。但不同的是CCERT传感器场域无负灵敏区，这是由于离散相会使电场线重新分布，对于ECT传感器，其激励电极以外的其它电极同时接地，可能会造成某些检测电极上的电场线减少，由此产生负灵敏区。但由于本研究CCERT所采用的数据采集模式中只有检测电极接地，其它电极悬空，因此检测电极上的电流线不会因为电流线重新分布而减少，所以CCERT的敏感场无负灵敏区。

2 传感器设计

本节首先利用实验数据对仿真建立的有限元模型进行验证，之后分别讨论了两种不同结构的传感器模型对测量值的影响，即屏蔽罩传感器模型与屏蔽罩及径向电极传感器模型(如图6)。最后，在确定了传感器的基本模型后，对屏蔽罩尺寸进行了优化。

2.1 基础模型的仿真与实验对比

首先通过实验来验证仿真所建立的有限元模型。传感器管道内径R1=55 mm，外径R2=57 mm，电极夹角θ=25°，电极长150 mm，管壁相对介电常数 εpipe=6，连续相(自来水)电导率 120 μs/cm，离散相电导率0，相对介电常数为1。

图4表示实验与仿真的66组电阻值相对变化量的对比，其中电阻相对变化量λi，j定义为

图4 仿真与实验的电阻变化量对比

由于CCERT灵敏场与ECT类似，因此初步判断ECT图像重建算法适用于CCERT。基于CCERT的灵敏场并结合ECT的线性反投影(LBP)图像重建算法，分别利用仿真及实验的66组电阻值获得管道截面的电导分布图像，如图5所示，其中图像中黑色区域表示离散相。由重建的图像分析可得，LBP算法基本适用于CCERT内部场域电导分布的图像重建。

图5 仿真与实验数据的重建图像对比

通过对基础仿真模型与实验模型的测量数据以及后续的重建图像对比可以得出，通过仿真建立的模型与实际模型基本吻合，因此可以基于该模型对实际传感器设计进行研究。

2.2 屏蔽罩传感器模型分析

为了减小外界电磁场对传感器以及检测电路的影响，首先设计了屏蔽罩模型，即在电极阵列外部安装与管道轴向平行的屏蔽罩，如图6(a)所示。但接地屏蔽罩必然会引起传感器场域内部电流线的重新分布，从而影响检测值大小。以下以典型空间位置的六组电极对间测量值为研究对象，即1－2、1－3、…、1－7这六组电极对间的测量值，通过对比两种不同尺寸的屏蔽罩及无屏蔽罩模型下这六组值的变化情况，进一步分析屏蔽罩对传感器内部场域的影响。

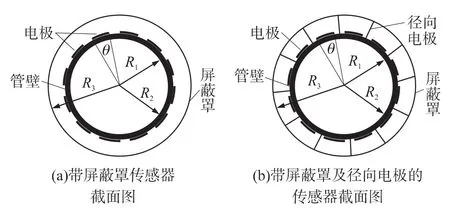
图6 传感器外安装屏蔽罩

如图6(a)所示，R2表示管道外半径，R3表示屏蔽罩半径，设h=R3－R2，即h表示沿管道径向屏蔽罩与管道外壁间的距离。

图7 屏蔽罩对6组典型电阻值的影响

从图7可以得出，两种尺寸的屏蔽罩都会使激励检测电极对间等效电阻值增大，且当屏蔽罩与外管壁间距离越小时影响越大。这是由于当屏蔽罩与管壁间距离较小时，屏蔽罩与其它悬空电极间会形成较大的寄生电容，使一部分电流线通过悬空电极流向屏蔽罩，造成检测电极上的电流线减少，从而改变之前建立的传感器等效模型，对系统测量产生影响。因而，在传感器空间允许的条件下，应尽量增大屏蔽罩尺寸。

2.3 径向电极传感器模型分析

径向电极的传感器模型如图6(b)所示，径向电极同时与管壁及屏蔽罩接触，指向管道截面圆心，轴向与传感器电极同长。在简化模型下，每组激励检测电极对间可等效为如图2所示的耦合电容与电阻的串联，但在管道外部激励检测电极间也会通过空气形成外部寄生电容Cp，等效电路如图8所示。并且由于相邻电极对空间距离最近，所以此寄生电容对相邻电极对的影响较其它电极对的影响大，对于本研究采用的传感器模型，会引起等效电阻值大约4%的相对变化。由于CCERT传感器结构与传统ECT类似，ECT检测中也存在同样问题，因此借鉴ECT传感器设计经验，希望通过安装接地的径向电极来降低这种影响，以下主要分析径向电极对CCERT传感器性能的影响。

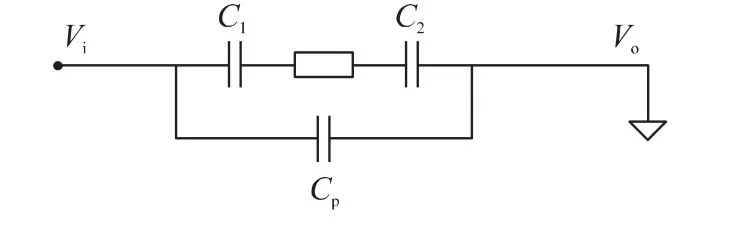
图8 原始模型电极对间等效电路图

当安装径向电极后，激励和检测电极对间等效电路如图9所示，其中Cs1与Cs2分别表示激励检测电极与屏蔽罩间的等效寄生电容；Cp1与Cp2分别表示激励检测电极与径向电极间的等效寄生电容。激励电极外部的寄生电容所在通路可看作检测电路的另外一个支路，而检测电极外部的寄生电容两端处于等电势状态，对测量电路无影响，由此即可抑制外部寄生电容对检测电路的影响。

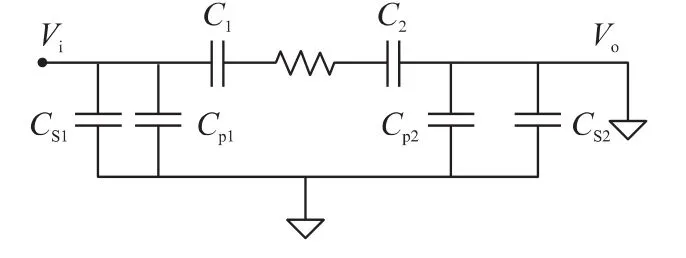
图9 安装有径向电极及屏蔽罩电极对间等效电路

以下仿真研究了不同尺寸的径向电极模型对各电极对间等效电阻值的影响，并与无屏蔽罩的原始模型，有屏蔽罩无径向电极模型的相应电阻值进行对比。图10(a)、10(b)、10(c)分别表示径向电极长度h为10 mm、30 mm和80 mm时，三种模型的6组典型电极对间的等效电阻值。由图10可以得出，当传感器安装有径向电极后，均会使等效电阻值急剧增大，与原始模型相比，电阻值的最大相对变化量均超过200%。对电阻值急剧增大的原因分析为，当径向电极安装在管壁外之后，径向电极都接地，且与电极间距离很小，约2 mm，径向电极与悬空电极通过空气会形成耦合电容，因此流向检测电极的电流必然减少，对等效电阻值产生影响。比由于外部空气耦合电容对等效电阻值造成的影响大很多。因此，从降低对电阻测量影响的角度考虑，不采用有径向电极模型。

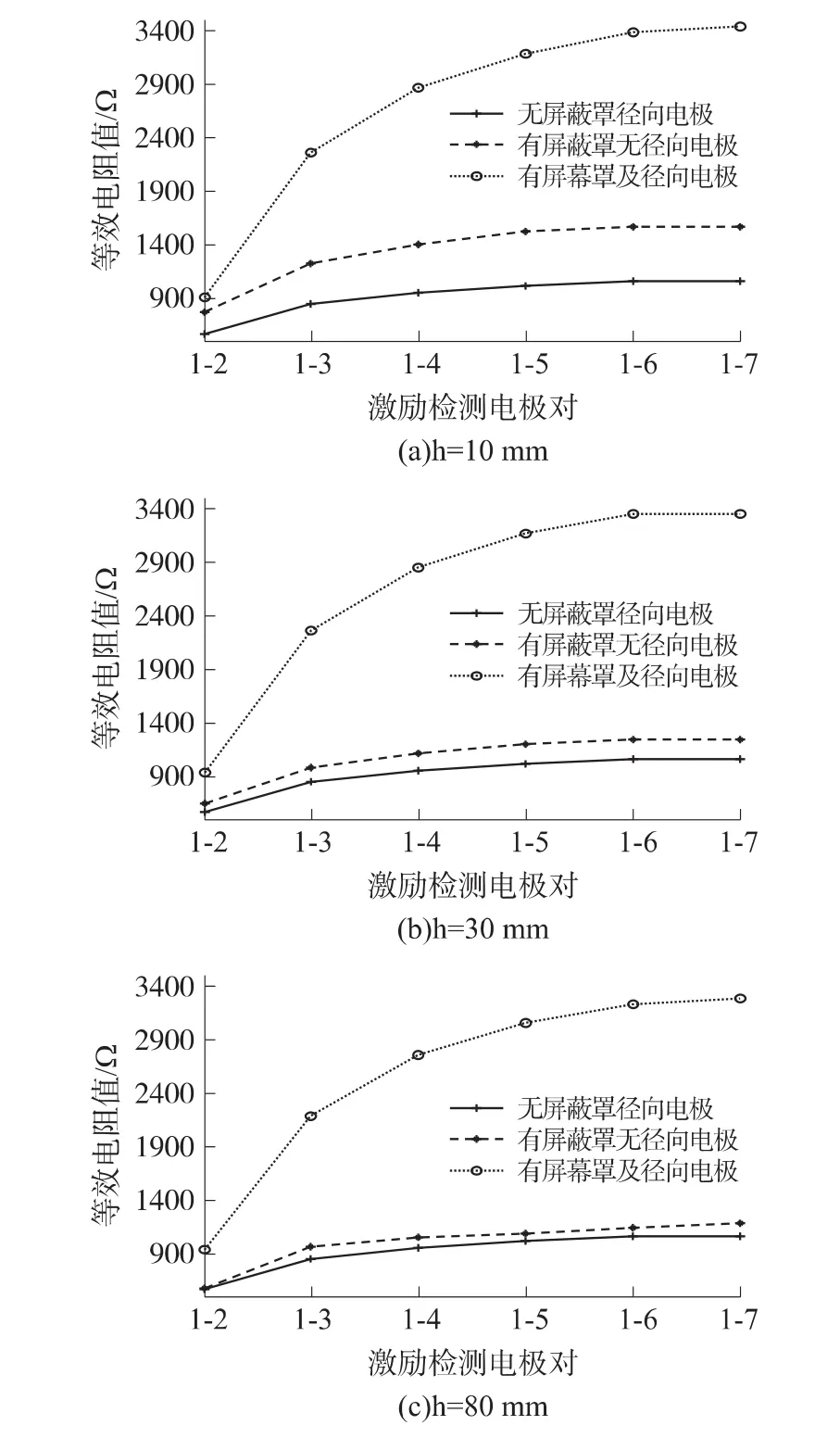
图10 有径向电极的6组典型电极对间等效电阻值

2.4 屏蔽罩尺寸优化

在确立了传感器的基本模型后，本节主要研究不同尺寸的屏蔽罩对各典型电极对间等效电阻值的影响，从而为屏蔽罩选取提供依据。以屏蔽罩与管道外壁距离h为研究对象，分析每种尺寸屏蔽罩模型中6对典型等效电阻值的最大相对变化量。图11表示h为10 mm、20 mm、30 mm、60 mm、80 mm 和120 mm 时等效电阻值的最大相对变化量。由图11可得，随着屏蔽罩尺寸的增加，屏蔽罩对等效电阻值的影响逐渐降低。当h为10 mm时，等效电阻值的最大相对变化量达到50%。随着h增大到120 mm，相对变化量降低到6%。因此在设计传感器屏蔽罩时，当条件允许时，应尽量选择较大尺寸的屏蔽罩，从而降低其对内部场域的影响。但增大屏蔽罩尺寸就必然使整个传感器体积增大，会对系统的紧凑性及安装或应用造成一定影响。因此可根据实际需要，以及检测电路的工作范围选择相应尺寸的屏蔽罩。

图11 各尺寸屏蔽罩的最大电阻值相对变化量

3 结论

首先建立了CCERT传感器场域数学模型，并将仿真建立的传感器有限元模型与实验模型进行对比，证明该模型与实际模型基本吻合，基于该模型的传感器设计及优化具有实际意义。

(1)为了降低外部电磁场的影响以及保护传感器电极，在基础模型的基础上，首先研究了带屏蔽罩传感器模型对系统测量值的影响。分析表明，屏蔽罩会令内部场域电流线重新分布，从而改变传感器等效模型，使检测电流减小，等效电阻值增大。

(2)研究了径向电极模型对系统测量值的影响。经仿真分析，各种尺寸的径向电极都会使检测电流降低，等效电阻值急剧增大，最大相对变化量均超过200%。因此在传感器设计时，建议不采用径向电极模型。

(3)最后，对屏蔽罩尺寸进行了优化，结果表明，对于本研究所采用的传感器模型及内部被测介质，当屏蔽罩与传感器外管壁间距离增大到120 mm时，电阻值的最大相对变化量降低为6%。

综上所述，本研究能够为传感器优化设计提供重要的依据。

［1］Beck M S，Williams R A.Process Tomography:a European Innovation and Its Applications［J］.Meas.Sci.Technol.，1996，(7):215－224.

［2］李海青，黄志尧.特种检测技术及应用［M］.杭州:浙江大学出版社，2000，1－9.

［3］Gas B，Demjanenko M，Vacik J.High-Frequency Contactless Conducti-vity Detection in Isotachophoresis［J］.J.Chromatogr，1980，(192):253－257.

［4］Zemann A J，Schnell E，Volgger D，et al.Contactless Conductivity Detection for Capillary Electrophoresis［J］.Anal.Chem.，1998，(70):563－567.

［5］Da Silva J A F，Do Lago C L.An Oscillometric Detector for Capillary Electrophoresis［J］.Anal.Chem.，1998(70):4339－4343.

［6］Kuba P，Hauser P C.A Review of the Recent Achievements in Capacitively Coupled Contactless Conductivity Detection［J］.Anal.Chim.Acta，2008，607(1):15－29.

［7］Pumera M.Contactless Conductivity Detection for Microfluidics:Designs and Applications［J］.Talanta，2007，74(3):358－364.

［8］Huang Z Y，Jiang W W，Zhou X M，et al.New Method of Capacitively Coupled Contactless Conductivity Detection Based on Series Resonance［J］.Sensors and Actuators B，2009，(143):239－245.

［9］Wang B L，Huang Z Y，Ji H F，et al.Towards Capacitively Coupled Electrical Resistance Tomography［C］//In Proc:6th World Congress on Industrial Process Tomography，Beijing，China，2010，1574－1577.

［10］XIE C G，HUANG S M.Electrical Capacitance Tomography for Flow Imaging:System Model for Development of Image Reconstruction Algorithms and Design of Primary Sensors［J］.IEE.Proc.G，1992，139(1):89－98.

［11］问雪宁，王化祥，胡理.基于ANSYS的ECT阵列电极三维优化设计［J］.传感技术学报，2007，20(7):1639－1643.

［12］颜华，邵富群，王师.电容层析成像传感器的优化设计［J］.仪器仪表学报，2000，21(2):139－145.

［13］孙强，石天明，刘景，等.ECT传感器结构影响分析［J］.自动化与仪器仪表，2008(6):83－85.

［14］胡松钰，王保良，黄志尧，等.高速电阻层析成像数据采集系统设计［J］.传感技术学报，2008，21(1):79－82.

［15］Wang Y，Sha H，Ren C S.An Optimizing Design Method for Electrode Structure Parameter of Electrical Impedance Tomography［C］//Engineering in Medicine and Biology 27th Annual Conference，Shanghai，China，2005:1525－1528.

［16］Kotre C J.A Sensitivity Coefficient Method for the Reconstruction of Electrical Impedance Tomograms［J］.Clin.Phys.Physiol.Meas.，1989，10(3):275－281.