基于有限元法的MEMS加速度计热应力分析*
游侠飞,吴昌聚,郑阳明,金仲和
(1.浙江大学信息与电子工程学系,杭州310027;2.浙江大学航空航天学院,杭州310027)
微机电系统MEMS(Micro Electro-Mechanical Systems)是由机械、电子、光学及其他一些功能元件,集成在单片或多个芯片上,构成对声、光、热、磁、运动等自然信息进行感知、识别、控制和处理的微型智能系统[1]。MEMS惯性传感器具有成本低、体积小、可靠度高、易于批量生产等优点。电容式加速度计作为MEMS惯性传感器的典型代表具有温度系数小、稳定性好、灵敏度高、可以通过静电回复力工作在力平衡模式等优点,是目前研究最多的一种加速度计[2],被广泛运用在航空航天、惯性导航、消费电子、汽车电子和地质勘探等关系国计民生的各个领域[3-4]。
电容式加速度计在加工过程中受材料性能,所连接的基底,边界条件,工艺过程和参数等条件综合影响存在残余应力[5],而残余应力严重影响器件的成品率,可靠性和动力学性能[6]。所以分析电容式加速度计的残余应力的具体来源,研究其影响大小以及减小应力的方法具有非常重要的意义。
从残余应力的来源来看,残余应力可分为本征应力和热应力。本征应力有微晶聚结,晶粒缺陷,掺杂,空位湮没等多种来源,其共同点是改变了材料内部的原子和分子间距,造成材料组织密度不均匀,局部晶格失配[7-8]。本征应力一般情况下不能完全消除,但可以通过改善工艺条件来进行有效控制和减小。热应力主要是由于多层材料热胀系数的不匹配以及器件温度的不均匀造成的,相应的变化规律一般可以根据公式计算或者仿真求解获得。
本文以MEMS电容式加速度计为模型,基于有限元热结构耦合场分析方法,对残余应力对器件的影响进行了建模仿真分析,总结了相关规律,并与既有实验测试结果进行比较,分析讨论了本征应力的可能影响因素,并从工艺的角度提出了相应的改良建议。为下一步加速度计温度补偿模型的完善以及加速度计的改版设计提供了一定的理论及实验依据。
1 基本理论
图1为本课题组研制的电容式MEMS加速度计的结构原理示意图。栅形可动电极和叉指固定电极构成了一个电容器,这两块极板对应的是敏感质量块和基底玻璃上上溅射的铝电极。
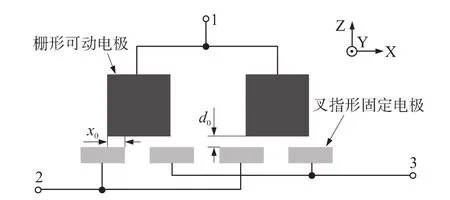
图1 加速度计结构示意图
MEMS电容式加速度计是由多层不同材料组成,由于不同材料存在热膨胀系数的不匹配,当温度变化时,器件中便会产生应力,即为热应力的主要来源[9]。对于二维各向同性的弹性材料来说,热应力可通过公式1计算获得[10]。
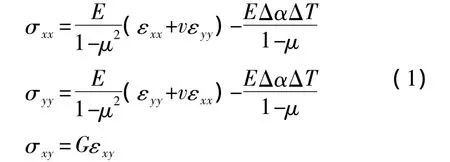
其中σij和εij分别为应力和应变,E、G和μ分别为杨氏模量、剪切模量和泊松比,Δα为薄膜和基底材料的热膨胀系数之差。此式具有较大的局限性[11],对于较为复杂的结构,如本课题所研制的器件,热应力不能通过此公式直接计算获得。本文则是借助于有限元耦合场分析法求解热应力,对热应力带来的MEMS电容式加速度计性能变化进行分析。
当加速度计没有受到加速度时,可动电极在初始位置,加速度计的初始电容值的大小是:

式中,n为栅电容的个数,y0为交叠长度,x0为交叠宽度,d0为电容间隙。当环境温度变化,由于器件材料本身的温度特性以及热应力的综合影响,加速度计的结构尺寸将发生变化。假设加速度计交叠宽度,交叠长度以及电容间隙的变化分别为Δx,Δy和Δd,则此时加速度计检测电容为:
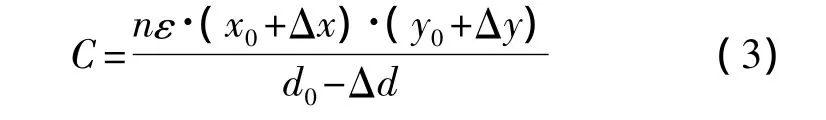
由于加速度计在结构上前后左右对称,所以采用实际结构的1/4建模,如图2所示。中间的硅质量块通过U型梁与外框连接,外框与玻璃基底通过阳极键合工艺连接在一起。

图2 加速度计1/4实体模型
2 残余应力对MEMS加速度计性能的影响
加速度计的主要部件的结构尺寸如表1所示。

表1 加速度计模型参数
加速度计各个结构的材料在室温(25℃)时的属性如表2 所示[12]。
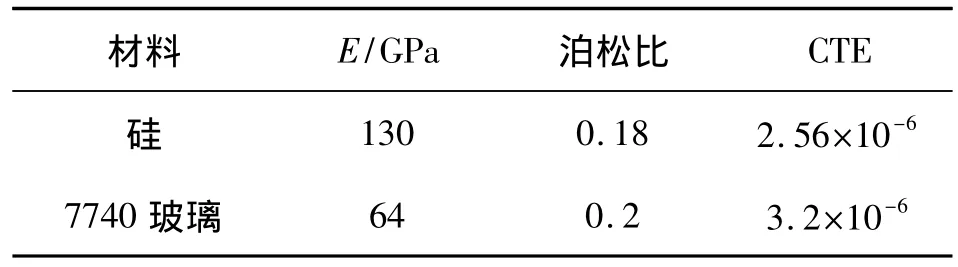
表2 模型中材料的属性(25℃)
需要注意的是硅和7740玻璃的热膨胀系数都是温度的函数,随着温度变化,两种材料的不匹配度也在不断变化,且变化规律直接影响键合温度和结构释放温度的选择。图3所示为Pyrex7740玻璃与硅材料热膨胀系数与温度的关系曲线[13]。
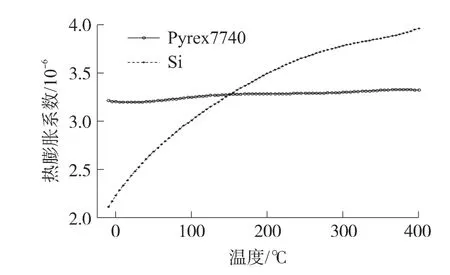
图3 硅与7740玻璃热膨胀系数温度关系曲线
2.1 热应力随温度变化规律
以室温25℃为参考温度点,在25℃ ~65℃范围内,加载结构约束和温度载荷求解计算获得加速度计热应力,取每种温度载荷下的最大应力值作为参考绘制热应力和温度关系曲线如图4所示。从图4可以看出,热应力随着温度的升高而增大,且两者之间基本呈线性关系。分析原因是温度升高后,由于键合材料的热膨胀系数的不匹配,两材料之间存在相互约束作用而产生热应力,温度升高越多,两者之间的约束作用就越强烈,最终导致了热应力的增大。而在此温度范围内,两键合材料热膨胀系数的失配度波动较小,所以基本呈线性变化。

图4 加速度计热应力-温度曲线
2.2 热应力对加速度计的影响
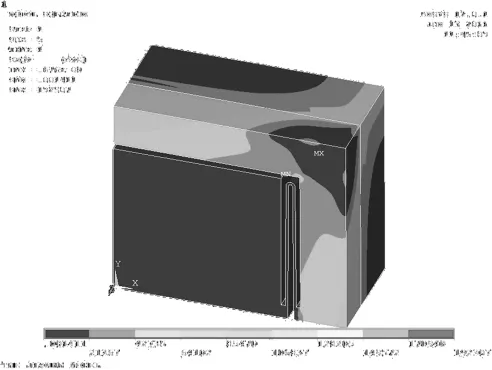
图5 加速度计等效应力分布图
图5为加速度计以25℃为基准,升温1℃时的等效应力分布图。从图中可以看出,应力主要集中在键合外框处,相对的整个质量块上的应力都非常小且均匀。说明加速度计质量块上所有节点具有相同的位移特征,故选取中心点作为样本点来计算热应力对加速度计性能的影响。在25℃~65℃的温度范围内,分别提取样本点的x、y、z 3个方向的位移,获得数据如表3所示。

表3 仿真初始数据
将表3中数据代入式(3)中可得受热应力影响下的加速度计初始电容。根据数据得到加速度计初始电容温度-电容值的拟合曲线为:C=1.0676×10-16×t+4.3308×10-12(F),如图6 所示。加速度计初始电容的温度系数为:
1.0676 ×10-16/4.3308×10-12=24.7×10-6/℃
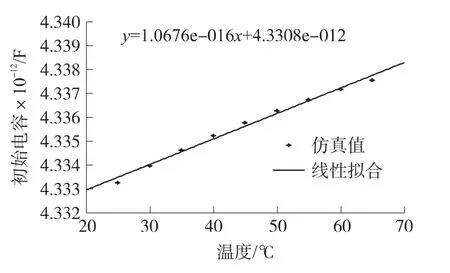
图6 初始电容随温度变化曲线
3 实验测试
由于加速度计工作在静止状态下,因此传感器内部的静态检测电容随温度的变化将影响加速度计系统的零位输出。测试原理框图如图7所示。
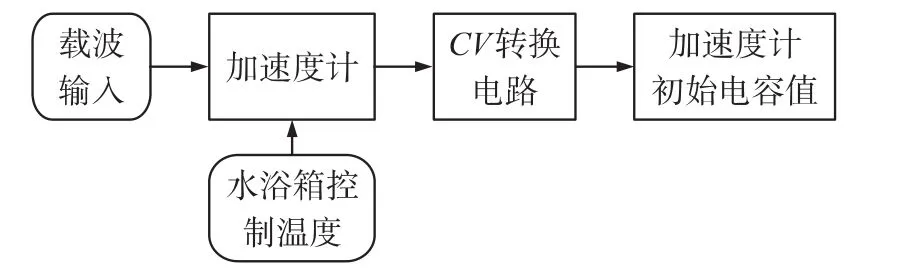
图7 实验测试原理框图
测试原理电路图如图8所示。载波信号Vc接到一对差动电容的公共端,差动电容的另外两端分别接到两电容反馈运算放大器的反相输入端,两个运算放大器的输出端分别接到仪表放大器的正相和反相输入端。
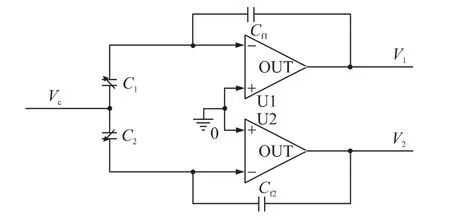
图8 测试原理电路图
运算放大器的输出可以表示为

由式(4)和式(5)可知通过测量两路CV电路的输出即可计算出加速度计对应的初始电容值。
在25℃~65℃范围内,采用水浴箱作为控温装置,每隔5℃测试一次加速度传感器系统中的两路CV转换电路输出信号的幅度,统计随温度的变化来间接获得加速度计内部初始检测电容的温度特性。总共对3个加速度计样品进行了测试,测试结果列于表4中。

表4 加速度计初始检测电容及其温度系数
4 结果与讨论
由表4可见,同一型号的加速度计个体之间在性能上存在较大差异,说明加速度计目前的加工工艺过程存在较大的误差。从表中还可以发现同一器件内部的两个初始检测电容的容值也不同。这是由于加工过程中光刻对准标记并没有完全对准,传感器封装过程的不理想,以及栅电极和铝电极表面的不平整也会引起C01和C02的大小不同。表4中的测试结果也表明同一加速度计器件内部的两个初始检测电容的温度系数也不一致,且远高于前面所分析过的热应力所造成的影响。
通过对仿真结果和测试结果的比较以及器件个体的差异性说明在目前课题组加速度传感器的工艺条件下,热应力不是影响器件性能的主要因素,仿真模型中没有考虑到的一些物理效应以及工艺误差可能是引起加速度计电容温度系数的主要因素。
首先,在热应力仿真分析时,没有考虑工艺误差以及本征应力对器件的影响。加速度计加工过程中存在一定的非理想因素,高温氧化、高温键合和结构释放等工艺也都会使结构产生一定的残余应力。测试结果也表明个体工艺误差不容忽视,所以必须对现有的工艺条件进行改善。
针对课题组加速度计目前的制备工艺提出以下工艺改良措施:
①采用退火等热处理工艺[14]目前课题组的加速度计制备工艺中没有引入退火工艺,增加退火工艺可以使材料组织密度更均匀,组织缺陷减少,有效减小氧化,掺杂等工艺引入的残余应力。
②调整键合以及结构释放温度[13,15-16]硅和7740玻璃的热膨胀系数都是温度的函数,见图3,两者之间存在一个最佳的配比可以使在结构释放时热应力达到最小,以期结构达到完美释放的效果。比如针对硅玻璃键合,两材料在300℃进行键合,当其冷却到25℃时,两材料拥有相同的自由收缩量,结构中热应力达到最小值,此时进行结构释放可以实现较理想的释放效果。而在其他温度下释放,则会由于结构中存在较大的热应力而达不到理想的释放结果。
③对结构进行分步释放 一次成形的结构释放法难免会因为残余应力的作用使结构产生微小形变,分布释放法基于去除材料释放应力的原理,对前几步的结构释放进行时效处理,有效释放残余应力,使结构释放达到理想效果。
5 结论
本文以MEMS电容式加速度计为模型,基于ANSYS有限元软件的耦合场分析方法,通过建模仿真分析,总结了器件中热应力随温度的变化规律,在25℃~65℃范围内热应力随温度变化基本呈线性关系。归纳了器件初始电容受热应力影响的温度特性曲线,获得其温度系数为24.7 10-6/℃,并与实测结果相比较,发现在目前工艺条件下热应力不是影响器件性能的主要因素。提出了增加退火工艺,调整键合温度以及采用分步结构释放法等工艺改进措施,为下一步加速度计温度补偿模型的完善以及加速度计的改版设计提供了一定的理论及实验依据,从而可以大大降低设计成本,大幅度缩短产品的设计时间。
[1] Stephen D S.微系统设计[M].北京:电子工业出版社,2004:330-351.
[2] Smith J H,Montague S,Sniegowski J J,et al.Embedded Micro-mechanical Devices for the Monolithic Integration of MEMS with CMOS[C]//Electron Devices Meeting,International.1995:609-612.
[3] Clark W A.Surface Micromachined z-Axis Vibratory Rate Gyroscope[C]//Hilton Head Island.Technical digest of the Solid-State Sensor and Actuator Workshop,South Carolina:1996:283-287.
[4] 姚素瑜,秦明,黄庆安.集成气象芯片中热应力对压力膜影响的有限元分析[J].传感技术学报,2006,19(5):1868-1870.
[5] Chen K.Techniques in Residual Stress Measurement for MEMS and Their Applications[J].2006:1252-1328.
[6] 虞益挺,苑伟政,乔大勇.微机械薄膜残余应力研究[J].微细加工技术,2005(2):46-50.
[7] Ohring M.The Materials Science of Thin Films[M].Boston:Academic Press,1992.
[8] Doerner M F,Nix W D.Stresses and Deformation Processes in Thin-Films on Substrates[J].Critical Reviews in Solid State and Materials Sciences,1988,14(3):225-268.
[9] Cheng-Hsin C,Wen-Hui L,Sony L.Thermal Analysis under Different Packaging Processes for MEMS Device with Diaphragm[C]//Electronic Materials and Packaging,International Conference,2008:153-156.
[10] Boresi A P.Elasticity in Engineering Mechanics[M].John Wiley and Sons,2010.
[11]王锡明,王军军,周嘉.多层薄膜微结构热应力计算[J].微细加工技术,2007,2(2):20-23.
[12] Lindroos V,Tilli M,Lehto A,et al.Handbook of Silicon Based MEMS Materials and Technologies[M].William Andrew,2010.
[13] Fung C D.Micromachining and Micropackaging of Transducers[M].New York:Elsevier Science Pub.Co.,1985:41-61.
[14] Chen K,Zhang X,Lin S.Intrinsic Stress Generation and Relaxation of Plasma-Enhanced Chemical Vapor Deposited Oxide During Deposition and Subsequent Thermal Cycling[J].Thin Solid Films,2003,434(1-2):190-202.
[15]李平,石云波,郭涛,等.MEMS高g加速度传感器封装热应力的研究[J].传感技术学报,2010,23(12):1695-1699.
[16] 黄庆安.硅微机械加工技术[M].北京:科学出版社,1996:215-216.

