基于磁流变阻尼器的触觉反馈系统

赵晓妍

(黑龙江科技学院 电气与信息工程学院,哈尔滨 150027)

基于磁流变阻尼器的触觉反馈系统

赵晓妍

(黑龙江科技学院 电气与信息工程学院,哈尔滨 150027)

针对传统触觉反馈系统安全性差、响应时间长、容易失真等问题,设计一种以磁流变阻尼器为核心的触觉反馈系统,并基于 Bingham模型推导了磁流变阻尼器的输出阻尼力计算公式。Simulink仿真结果表明:磁流变阻尼器的位移、速度与阻尼力的关系符合 Bingham模型,体现较好的动态性;当电流控制器输出电流为 0～1 A,速度为 10 mm/s时,输出阻尼力大小连续可调,最大阻尼力为 19.6 N,最小为 2.435 4 N。理论和仿真结果吻合,验证了该触觉反馈系统的可行性。

触觉反馈;磁流变阻尼器;Bingham模型;Simulink

触觉反馈是一种重要的感知模式,其技术已广泛应用在遥感操作机器人系统、远程外科手术等领域。传统的触觉反馈系统采用电机或其他执行机构的驱动方式,这些方式存在安全性较差、响应时间长、容易失真等问题[1]。磁流变阻尼器具有良好的可控性,不仅能实现触觉反馈系统的智能控制,还可提高其反应速度和安全稳定性,具有重要的应用和研究价值[2]。笔者设计了一种以磁流变阻尼器为核心的触觉反馈系统,通过电流控制实现反馈力的连续可调。

1 触觉反馈系统结构及工作原理

基于磁流变阻尼器的触觉反馈系统结构如图 1所示。该系统主要包括以 DSP为控制中心的数据采集模块、磁流变阻尼器、电流控制器三个组成部分。位移传感器和角度传感器与执行元件连接在一起,执行元件动作信息(位移和角度)通过传感器转换成电信号,再经A/D转换送入DSP进行运算控制处理。根据处理信号调节 PWM波形的占空比,控制电流控制器产生的电流,以改变磁流变阻尼器的磁场,从而产生相应的阻尼力。反应在操作杆上的力随电流变化,使操作者有不同的触觉感受,实现触觉反馈功能。

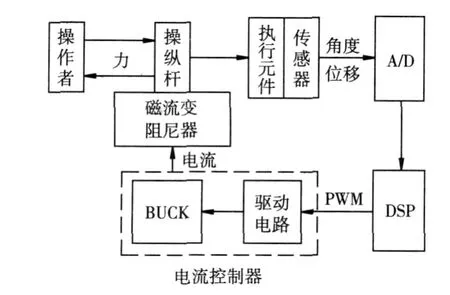
图1 触觉反馈系统框图Fig.1 Schematic of haptic system

2 磁流变阻尼器

触觉反馈系统的核心部分是磁流变阻尼器。操作杆与磁流变阻尼器中的活塞设置为固定连接、同步移动的形式,从而借助磁流变阻尼器将力的大小提供给操作者。

2.1 结构

磁流变阻尼器采用剪切阀式工作模式,其结构如图 2所示。活塞与缸筒之间有间隙,线圈通电后,间隙中的磁流变液受到磁场作用可以在毫秒级时间内转化为Bingham体[3]。当活塞运动时,磁流变液受到挤压而流过间隙,产生阀式运动和剪切作用。

图2 磁流变阻尼器结构Fig.2 Structrue ofM R damper

2.2 阻尼力计算

2.2.1 Bingham模型

剪切阀式磁流变阻尼器的阻尼力可以分解为剪切模式阻尼力和阀式模式阻尼力。活塞与缸体之间的间隙较小,一般取 1～2 mm,而磁流变阻尼缸体的内径、磁流变液工作区域有效长度远大于这一间隙,故可认为磁流变液是在两个平行极板之间流动。

由于磁流变液的动态本构关系非常复杂,而磁流变阻尼器动态阻尼力与磁场强度呈非线性关系,故文中依据简单的 Bingham模型进行计算。Bingham模型由一个线性黏滞阻尼器和一个库仑摩擦元件并联组成,如图 3所示。依据Bingham模型,稳态剪切场下的磁流变液本构关系可以近似描述为

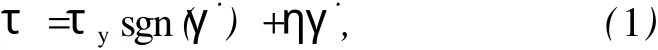
式中:τ——磁流变液的剪切应力;

τy——磁流变液的屈服强度,与磁场强度有关;

η——磁流变液的动力黏度系数;˙

γ——磁流变液的剪切应变速率。

根据式(1),Phllips提出磁流变阻尼器的力和位移的关系式

式中:F——磁流变阻尼器产生的力;

Fm——与磁场强度相关的屈服力;

F0——磁流变阻尼器气体蓄能器的气压产生的出力偏差,可忽略不计;

C0——磁流变液的阻尼系数;

v——活塞的相对速度[4]。

图 3 磁流变阻尼器的 B ingham模型Fig.3 Bingham model forM R damper

2.2.2 阀式阻尼力

根据平行极板的 Bingham模型,液体流变后会产生流动并在两极板上产生压差。设平板的宽度为b,取b为间隙的平均周长,即b=πD1。两极板间流体的体积流量qV可以由截面速度分布曲线沿y轴的积分乘以平板宽度b得到,即

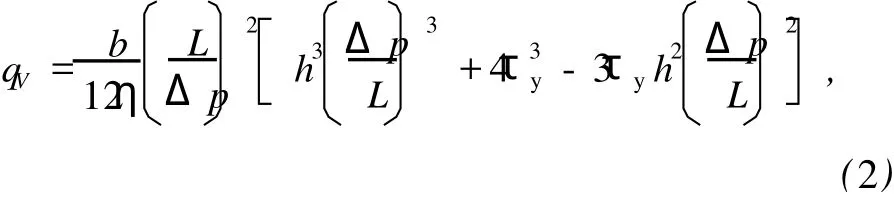
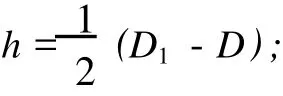
D——活塞的直径;

D1——缸体的内径;

L——磁流变液工作区域的有效长度。

对式(2)进行无量纲化处理,则

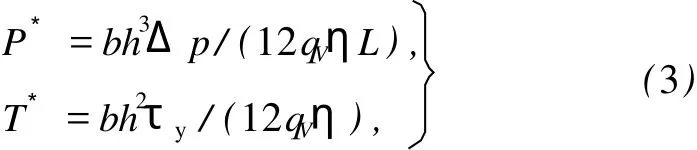
式中:P＊、T＊——无量纲化的压力差和屈服应力。

根据磁流变阻尼的参数进行计算后发现,T＊的取值比较小,与P＊存在近似关系,

由式(3)、(4)可得阀式阻尼器的阻尼力表示式,即

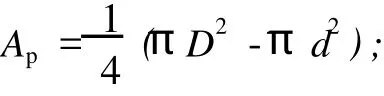
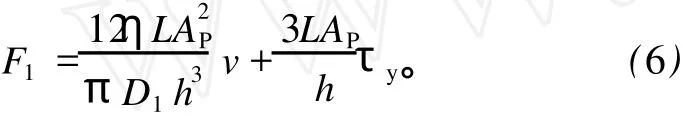
2.2.3 剪切式阻尼力

对于平行极板模型的阻尼力F2

由式(1)可得

将式(6)和式(7)联合,可以得到剪切阀式磁流变阻尼器的阻尼力

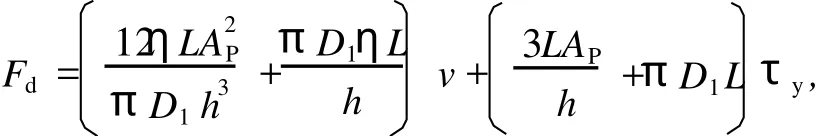
其中,第一项为黏滞阻尼力;第二项为库仑阻尼力,由磁场强度决定,是可控的,该项反映了磁流变阻尼器特殊的电控特性。由于h很小,剪切模式引起的阻尼力所占的比重较小,通常忽略不计。因此,磁流变阻尼器输出的阻尼力为

2.3 S imulink仿真

由式(8)可知,磁流变阻尼器输出阻尼力与很多因素有关,其中,间隙h、缸体内径D1、活塞杆直径d与阻尼力成反比;有效长度L、活塞的直径D与阻

d——活塞杆的直径。

当qV为磁流变液的体积流量时,qV=APv,式(5)可变为尼力成正比。一般h取 1～2 mm,动力黏度系数η取 0.2～1.0。根据触觉反馈系统要求,输出阻尼力一般在 4～20 N范围内。考虑系统的控制效果,确定磁流变阻尼器参数,如表 1所示。

表1 磁流变阻尼器基本参数Table 1 Basic parameters ofM R damper

屈服强度τy随磁场变化,与电流有关。因此,一般通过励磁线圈中电流的大小改变磁场强度,从而通过改变τy来控制阻尼力。根据表 1,计算得τy和控制电流I之间的关系式[5],

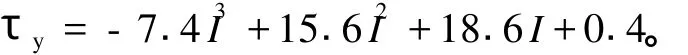
通过对磁流变阻尼器阻尼力、电流及速度关系的推导,建立磁流变阻尼器的 S imulink模型。对该模型施加频率为 1 Hz,位移为 10 mm的正弦振动激励信号x=0.1sin(2πt)时,输入不同的电流值,即可以得到磁流变阻尼器的阻尼力随位移、速度变化的关系曲线,如图 4、5所示。

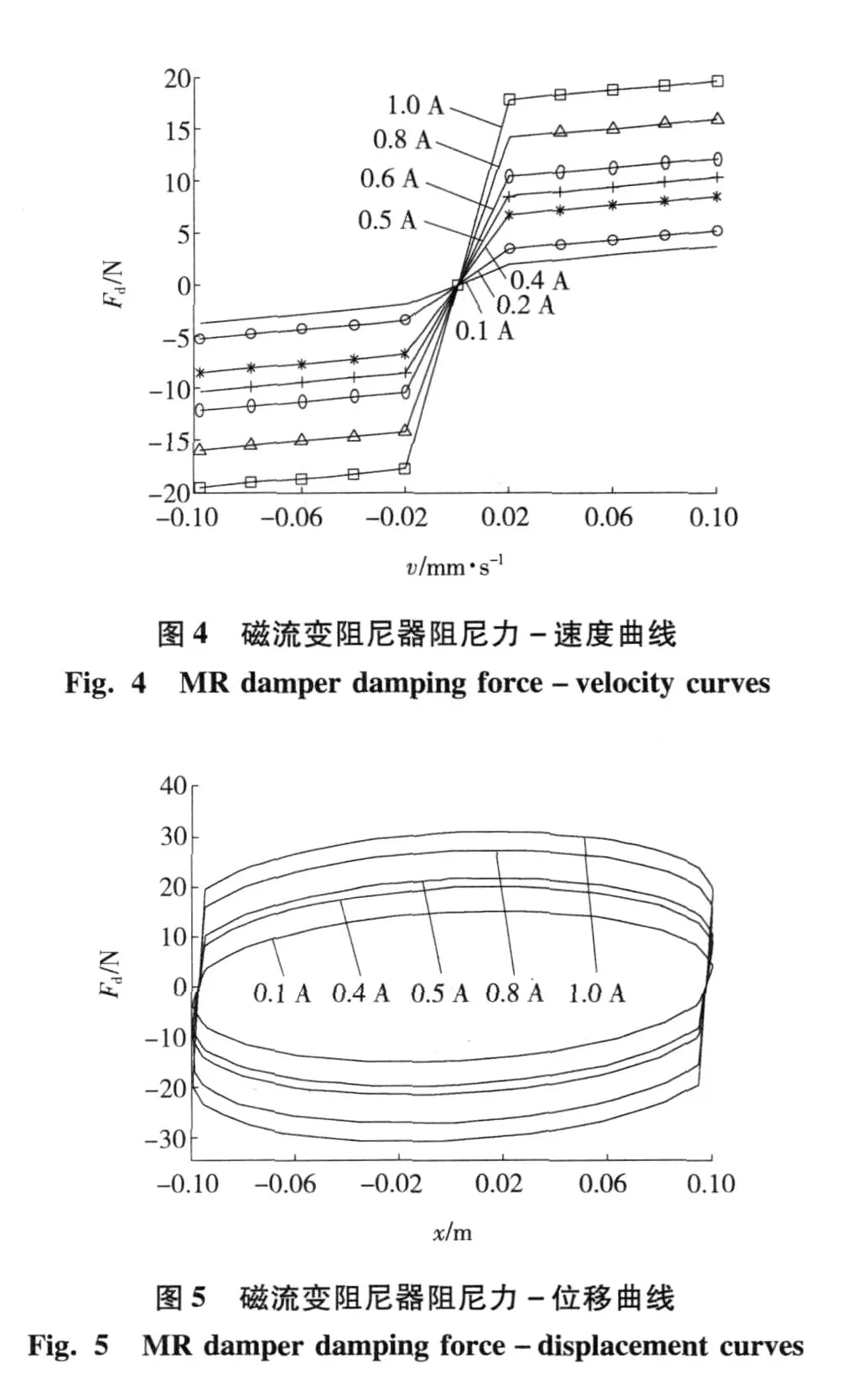
由图 4、5可以看出,阻尼力 -速度曲线符合B ingham本构关系,当速度、电流增大时,阻尼力及其范围明显增大;阻尼力 -位移曲线饱满,体现出较好的动态性能。

磁流变阻尼器阻尼力随电流变化的曲线如图 6所示。从图中可以看到,电流在 1.5A以下时与阻尼力满足线性关系,说明阻尼力的可控性良好,电流增大后阻尼力饱和。为保证安全和可控性,该阻尼器的最大励磁电流为 1.0A,产生的最大阻尼力为19.6N。当电流为 0A时,由式(8)计算的阻尼力为2.435 4N。

图6 v=10 mm/s时电流 -阻尼力曲线Fig.6 Current-damp ing force curve when velocity is 10 mm/s

3 触觉反馈的控制与实现

为了获得连续可调的电流,采用 DSP生成PWM信号,通过降压斩波直流变换电路,实现电流的控制[6-7]。系统要求电流控制器输出电流的变化范围为 0～1 A,具体电路如图 7所示。

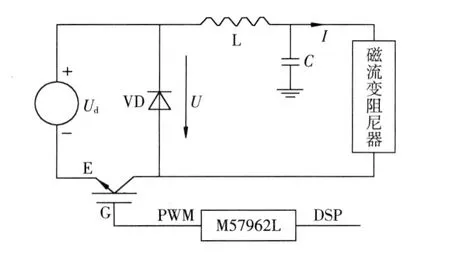
图7 PWM电流控制器Fig.7 PWM current controller

电路中的开关器件采用驱动功率较小的 IGBT,通过三菱的M57962L集成芯片驱动。由 DSP输出的 PWM波形经驱动芯片加载至 IGBT的栅极G端。当 PWM为高电平时,开关管 IGBT导通,二极管VD截止,电流经过 LC滤波电路后输送给磁流变阻尼器的励磁线圈;当 PWM为低电平时, IGBT断开,电流经过二极管形成回路。Ud为电路的输入电压,U为电路的输出电压,I为输出电流。通过DSP内部算法计算调整 PWM波的参数可使电路输出相应的控制电流,从而得到力反馈装置的输出阻尼力。

4 结束语

笔者设计了一种基于磁流变阻尼器的触觉反馈系统,并依据Bingham模型推导出该系统中磁流变阻尼器的基本参数和输出阻力的计算公式,确定了阻尼力与电流的关系。Simulink仿真结果表明,磁流变阻尼器的位移、速度与阻尼力的关系符合Bingham模型,且动态特性较好;当电流控制器输出电流为 0～1 A,速度为 10 mm/s时,输出阻尼力大小连续可调,最大阻尼力为19.6 N,最小为2.435 4 N,可以保证操作者的安全。理论与仿真结果验证了触觉反馈系统的可行性。

[1] 戴金桥,王爱民.新型智能材料在力/触觉反馈中的应用[J].测控技术,2007,26(7):3-6.

[2] 王爱民,戴金桥.基于液体智能材料的被动力反馈数据手套[J].测控技术,2007,26(11):10-12.

[3] YANG G,SPENCER B F,CARLSON J D,et a1.Large-scale MR fluid dampers:modeling,and dynamic performance considerations[J].Engineering Structures,2002,24(3):309-323.

[4] 邓志党,高 峰,刘献栋,等.磁流变阻尼器力学模型的研究现状[J].振动与冲击,2006,25(3):121-124.

[5] 顾 苗.冲击载荷作用下磁流变阻尼器缓冲控制算法研究[D].南京:南京理工大学,2006:19-25.

[6] 宋端坡,佘 红,王强锋,等.磁流变阻尼器阻尼力控制系统的设计[J].煤矿机械,2009,30(2):32-34.

[7] 潘之茂,刘佐民.基于 PC的磁流变阻尼控制器的研制[J].武汉理工大学学报,2002,24(8):67-68.

Haptic feedback system based on MR damper

ZHAO X iaoyan
(College of Electric&Infor mation Engineering,Heilongjiang Institute of Science&Technology,Harbin 150027,China)

A haptic feedback system with a core ofMR damper is designed in this paper,solving the problems of the traditional haptic feedback system with poor safety,long response t ime and easy distortion.The paper deduces the fo rmula ofMR damper dampingpower based on theBingham model.Simulation results indicate that the relations of the displacement,velocity and damping force ofMR damper are in accordance with Bingham model and show better dynamic characteristics.The controlled and continuous damping powerwill be produced by the haptic feedback system on the condition that the electricity output is from 0 to 1 A in current controller,and velocity is 10 mm/s.The max imum damping power is 19.6 N and the minimum is 2.435 4 N.That simulation results conform to the theory,proving the feasibility of the haptic feedback system.

haptic feedback;MR damper;Bingham model;S imulink

TP271.9

A

1671-0118(2011)02-0124-04

2011-01-26

赵晓妍(1979-),女,黑龙江省哈尔滨人,讲师,硕士,研究方向:电力电子、智能控制,E-mail:zhaoxiaoyan121@126.com。

(编辑荀海鑫)