偶数阶微分方程边值问题的上下解方法

王 刚, 朱思念

(中国矿业大学 理学院,江苏 徐州 221008)

偶数阶微分方程边值问题的上下解方法

王 刚, 朱思念

(中国矿业大学 理学院,江苏 徐州 221008)

针对实际应用中高阶微分方程的求解问题,讨论了一类偶数阶微分方程两点边值问题解的存在性,利用上下解方法,通过将 2n阶微分方程转化为二阶积分微分方程,得到其解的存在性定理,同时,在形式上推广了已知的四阶两点边值问题的结果。

微分方程;上下解方法;边值问题;存在性

0 引 言

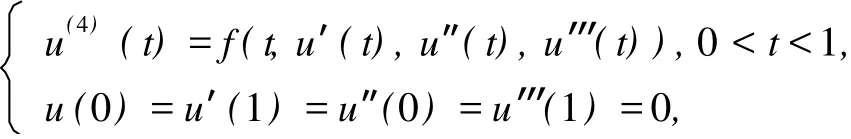
非线性高阶微分方程边值问题在应用数学和物理领域中具有深刻背景,其解的存在性有重要的理论和现实意义。关于偶数阶微分方程边值问题,目前多集中于讨论四阶微分方程边值问题解的存在性[1-7],其主要研究方法有上下解方法、单调迭代技术和不动点理论等。其中,白占兵[1]研究了四阶微分方程两点边值问题,通过降阶将其化为二阶微分 -积分方程,再利用上下解方法证明其解的存在性;张琴等[2]利用上下解方法和单调迭代技术考虑了一类四阶四点微分方程边值问题解的存在性;张兴秋[3]利用上下解方法和极值原理研究了一类具有积分边界条件的奇异四阶微分方程正解的存在性和唯一性。而对于任意偶数阶微分方程边值问题,研究其解的存在性问题较少。如郑惠军等[8]利用锥压缩与锥拉伸不动点定理,证明了一类 2m阶边值问题的正解存在性;梁思华等[9]利用上下解方法考虑了一类 2n阶多点边值问题解的存在性。受文献[1]启发,笔者研究 2n阶微分方程两点边值问题

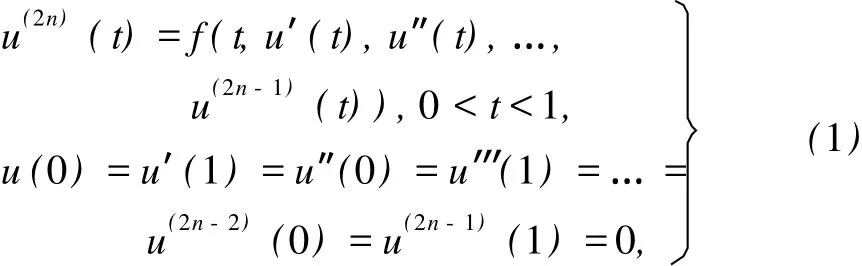
通过降阶和上下解方法,将其转化为积分微分方程,讨论其解的存在性。其中f:[0,1]×R2n→R是连续的。易知,当n=2时,问题(1)就转化为四阶两点边值问题,即文献[1]所讨论的结果,因此,文献[1]是文中的一个特例。

1 预备知识

2 主要结果

[1] BA I ZHANB ING.The upper and lower solution method for some fourth-order boundary value problems[J].Nonlinear Analysis, 2007,67(6):1 704-1 709.

[2] ZHANGQ IN,CHEN SHIHUA,LU J INHU.Upper and lower solution method for fourth-order four-point boundary value problems [J].Journal of Computational and Applied Mathematics,2006, 196(2):387-393.

[3] 张兴秋.奇异四阶积分边值问题正解的存在唯一性[J].应用数学学报,2010,33(1):38-50.

[4] DEL P INOM A,MANASEV I CH R F.Existence for a fourth-order boundary value problem under a two parameter non resonance condition[J].Proc AmerMath Soc,1991,112(1):81-86.

[5] CABADA A.The method of lower and upper solutions for second, third,fourth and higher order boundary value problems[J].J Math AnalAppl,1994,185(2):302-320.

[6] WEI ZHONGL I,PANG CHANGCI.The method of lower and upper solutions for fourth order singularm-point boundary value problems[J].J Math AnalAppl,2006,322(2):675-692.

[7] FENG HANY ING,JIDEHONG,GEWEIGAO.Existence and uniqueness of solutions for a fourth-order boundary value problem [J].NonlinearAnalysis,2009,70(10):3 561-3 566.

[8] 郑惠军,孔令彬.2m阶非线性边值问题的 Green函数与正解[J].大庆石油学院学报,2010,34(01):106-111.

[9] L IANG SIHUA,ZHAN JI HU I.Themethod of lower and upper solutions for 2nth-order multi-point boundary value problems[J]. NonlinearAnalysis,2009,71(10):4 581-4 587.

Method of lower and upper solutions for even-order boundary value problem s

WANG Gang,ZHU Sinian
(College of Sciences,China University ofMining&Technology,Xuzhou 221008,China)

Aimed at the solution to higher differential equation in practical application,thispaper discusses the existence of solutionsof two-point boundary value problem of a class of even order differential equation and describes the use of the method of upper and lower solutions to convert the 2n-order differential equation into second order integral-differential equation to obtain the existence theorems of solutions,alongwith the extension of the known results of fourth-order two-point boundary value problem in the fo rm.

differential equation;method of lower and upper solutions;boundary value problems;existence

O175.8

A

1671-0118(2011)02-0157-04

2011-02-21

王 刚(1985-),男,安徽省安庆人,硕士,研究方向:微分方程,E-mail:wangg0824@163.com。

(编辑王 冬)