光电稳定跟踪平台的载体运动耦合描述方法

李忠勤, 董 浩

(1.黑龙江科技学院 电气与信息工程学院,哈尔滨 150027;2.哈尔滨工业大学 控制与仿真中心,哈尔滨 150080)

光电稳定跟踪平台的载体运动耦合描述方法

李忠勤1, 董 浩2

(1.黑龙江科技学院 电气与信息工程学院,哈尔滨 150027;2.哈尔滨工业大学 控制与仿真中心,哈尔滨 150080)

针对载体运动的耦合机制及其角速度耦合模型不能准确描述角速度传递问题,采用理论建模的方法,分析了摩擦力矩与电磁转矩随载体运动的变化情况、控制系统的闭环作用下载体运动角速度的耦合机制。研究表明,捷联稳定方式下载体运动角速度存在1∶1传递,而直接稳定方式下载体运动角速度无 1∶1传递。旋转矩阵相应元素在捷联稳定方式下为 1,而在直接稳定方式下为 0。于是,按载体运动耦合情况建立了角速度耦合模型。该结果为制定有效的运载体角运动隔离方案提供了理论依据。

耦合机制;角速度传递;摩擦力矩耦合;直接带动耦合

0 引 言

稳定跟踪平台由于能隔离运载体角运动,不断测量平台姿态和位置的变化,精确保持动态姿态基准,并通过探测设备实现对机动目标自动跟踪,在导弹、飞机、战车、舰船中得到了广泛的应用。随着技术的不断发展,在航空光电侦察平台领域、机载和星载激光武器系统领域以及深空光通信领域需要高精度稳定平台。而深入分析运载体角速度耦合机制是建立高精度稳定平台的前提。

不考虑动力学耦合因素,载体的运动主要通过三种方式耦合给台体,即:直接带动耦合、摩擦约束耦合和几何约束耦合[1]。摩擦约束耦合是指通过平台环架支承轴的摩擦力矩将载体角速度传递给台体的过程,几何约束指通过平台支承轴和轴承侧面接触将载体角速度传递给台体的过程。目前仍存在如下两个问题。

(1)直接带动耦合存在多种认识:一是通过传动装置(在直接驱动方式下为刚性连接)的整体将载体角速度沿平台支承轴传递给台体[2];二是由反电动势产生的角速度传递[1,3],也有的将直接带动解释为摩擦约束[4],众说纷纭,表述不一。

(2)载体角速度耦合描述存在缺陷:以最简单的力矩电机直接驱动稳定瞄准线两轴平台为例说明问题。如图 1所示两轴稳定平台,定义载体坐标系b,方位环坐标系a,俯仰环坐标系f,方位环角θa,俯仰环角θf。设载体角速度ωb,方位环角速度ωa,俯仰环角速度ωf。

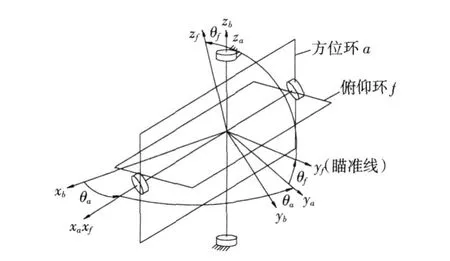
图1 两框架稳定平台Fig.1 Stabilizing platform of two frames

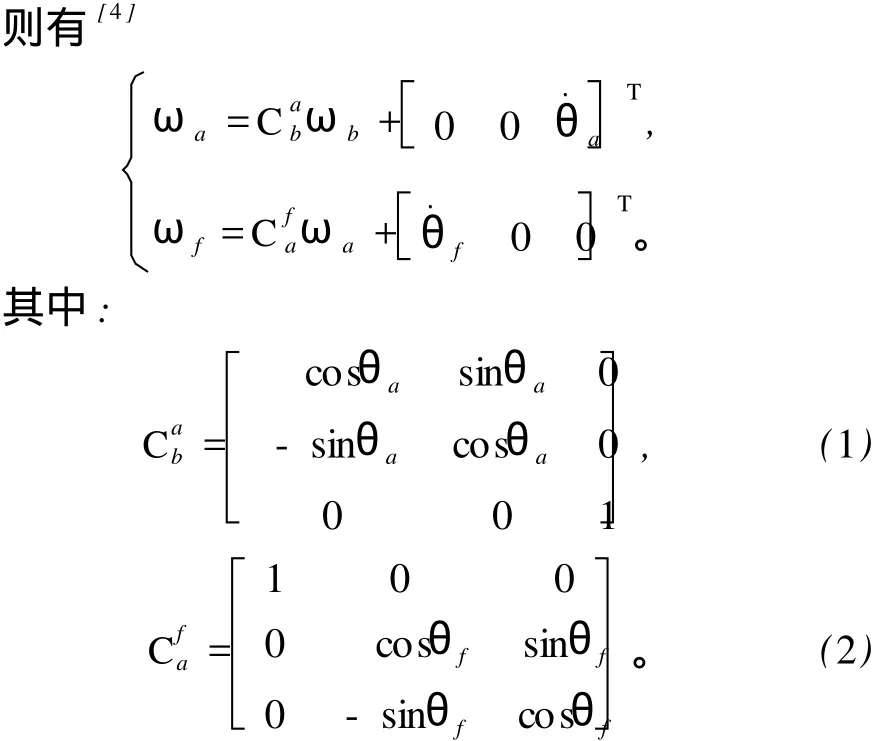
从物理意义考虑,存在如下问题:在方位环AZ方向ωbz在公式上看是1∶1传递的。然而在Z方向载体是通过电机轴与轴承相连,是活动非固连的,如何产成 1∶1的角速度传递以及如何对消该角速度,俯仰环也如此。这两个问题说明了目前对稳定平台的载体角速度耦合机制的认识尚不够明确统一。力是改变物体运动状态的原因,看物体运动状态变化首先要分析其受力情况,进行动力学分析,再对载体的运动耦合机制进行研究。

1 动力学分析及力矩变化

为简化分析,只取一个轴向并且假设载体仅作一维运动。以方位环为例,忽略轴弹性因素,忽略电机内部摩擦、磁滞力矩等相对小量作用,电机输出力矩为理想的电磁转矩。在AX、AY方向电机轴垂直与轴承为直接刚体固联,负载所受力矩无穷大,载体角速度按1∶1传递。在AZ方向负载受轴承摩擦力矩与电机电磁转矩作用。为便于说明问题,在分析一种力矩作用时忽略另一种力矩作用的影响。

1.1 摩擦力矩变化

方位环架受其支撑轴承摩擦力矩做用。假设摩擦力矩为最简单的库仑摩擦。设其值为Mf,当相对速度不为零时摩擦力矩为库仑摩擦Mc(Mc>0)方向与角速度方向相反,当相对速度为零时,摩擦力矩为多值非线性,设其为M:

J为负载转动惯量。

机械系统摩擦力矩扰动使得系统存在“死区”“平顶”,造成稳定平台稳定“尖峰”[3],是影响平台稳定精度的最主要原因。但是对于摩擦力矩影响的分析传统上只是建立在平台稳定到惯性空间零位基础上。

需要指出的是:(1)稳定并不一定稳定到零,跟踪状态下仍然存在稳定;(2)摩擦力矩的影响主要在于换向,即负载与载体——轴与轴承相对运动速度过零,摩擦力矩造成“死区”或者“尖峰”,摩擦为典型的非线性环节,其特性与相对运动速度有关,即与载体运动角速度、负载跟踪角速度有关,而载体角速度是独立的,所以不能只看摩擦对稳定到惯性空间零位的影响。

从式(3)可见,无论是稳定到零位,还是稳定于跟踪状态,摩擦力矩扰动的影响都应该看负载和载体的相对速度关系。

情况一:负载速度与载体速度存在换向。在过零时刻,摩擦呈非线性特征,载体角速度会通过摩擦力矩耦合到平台负载上。如果载体角加速度值有限,满足≤Mc,则摩擦力矩足以带动平台负载同载体一起同速运动,此时 Mf≤Mc,ωaz-ωbz=载体角速度按 1∶1传递到负载上;如果>Mc,则摩擦力矩不足以带动平台负载同载体一起同速运动,此时Mf=Mc,ωaz-ωbz=0,ω˙az< ω˙bz,载体角速度不能按 1∶1传递到负载上。在摩擦力矩作用下,平台负载随载体同向转动,摩擦力矩呈现直接带动作用。

情况二:负载速度与载体速度不存在换向。负载速度始终大于或小于载体速度,那么摩擦力矩为线性且始终没有变化。如果ωaz与ωbz方向相反或者ωaz与ωbz方向相同但数值较小,则Mf方向与ωbz方向相同,摩擦力矩起直接带动作用;如果ωaz与ωbz方向相同且数值较大,则 Mf方向与ωbz方向相反,摩擦力矩对ωbz起阻碍作用。

所以忽略电磁转矩情况下,摩擦力矩作用不一定产生直接带动作用。

实际中存在电机驱动力矩情况下,情况一表现为由于换向造成平台稳定尖峰;情况二表现为跟踪状态下电磁力矩同摩擦力矩相抵消,载体角速度不通过库仑摩擦力矩耦合到平台上。

1.2 电磁转矩变化

忽略摩擦等阻转矩影响,分析载体角运动对电磁转矩的影响。电机机身与载体固联,载体角运动使得电机内部磁场发生转动。则此时电机输出力矩驱动负载转速是相对于惯性空间还是相对于机身磁场,从直流力矩电机转矩平衡方程与电压平衡方程可以看得更加清晰,有

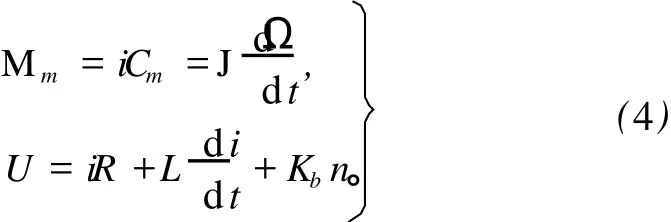
式中:Kb——电机反电势系数;

Cm——力矩系数;

JΣ——负载及电机转动部分转动惯量;

n——电机轴转速;

Mm——电机电磁转矩。

则问题表述为:在电机机身本身相对于惯性空间以角速度ωbz转动时,电机输出转矩Mm是如何变化的,Ω是相对惯性空间的物理量还是相对机身的物理量,n又如何。

(1)反电动势的影响

根据电磁感应定律,磁场中运动导体产生反电动势,反电动势大小与导体与磁场运动速度有关,即n为相对于机身的物理量。反电动势εb=Kb(ωazωbz),Kb为系数。可见,载体角运动引起反电动势变化,进而引起电流的变化,从而改变电磁转矩。

(2)磁场转动的影响

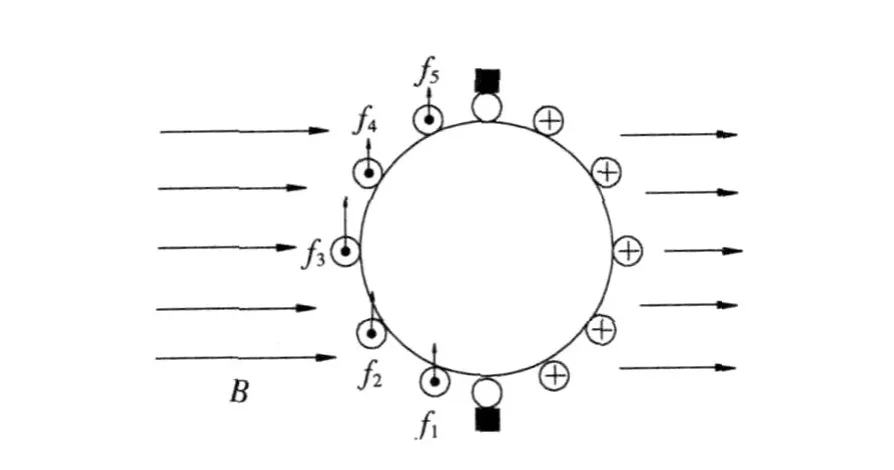
图2 电机机身转动工作原理Fig.2 Principle of electric motor body rotation

磁场的转动只是改变了电磁力的方向,并没有改变总的电磁力的大小,也没有改变电磁转矩,则式(4)中Ω为相对惯性空间的物理量。

所以载体角速度通过反电动势作用改变电机电枢电流,从而引起电机输出力矩变化,机身角运动对电磁力矩并无直接的刚性 1∶1传递作用。

综上所述,非稳定轴向载体角速度通过刚性连接直接传递到平台负载,载体运动速度存在 1∶1传递作用。稳定轴向为刚性连接,载体运动速度无1∶1传递作用,因此式(1)、(2)矩阵中的 1是否合适值得商榷。

载体角速度通过摩擦力矩及反电动势耦合到平台负载上,不同运动状态下摩擦扰动所起作用不同,摩擦扰动并不总是起直接带动作用;而反电动势所起的作用为直接带动作用,所以文中认为将直接带动耦合解释为反电动势耦合更恰当。

2 载体运动耦合机制及描述方法

通过以上分析可得平台没有速度闭环控制状态下的开环方框图,如图 3所示,它清楚的表述了摩擦干扰力矩、反电动势的传递方式:由于载体角运动引起的反电动势扰动为Kbωbz,在起作用下驱动平台和载体同向运动,是一种直接带动,开环状态下平台负载输出角速度为相对惯性空间物理量ωaz。

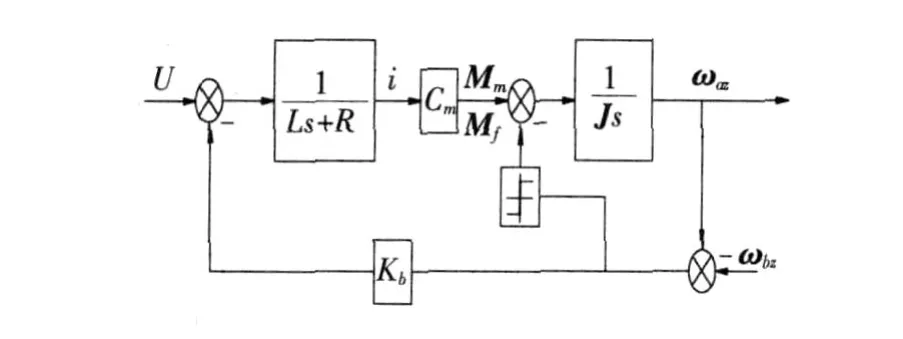
图 3 开环状态载体角速度传递框图Fig.3 Coupling of basement rotational speed at open loop

按陀螺安装方式不同稳定平台可分为捷联稳定式和直接稳定式[5],二者闭环控制作用不同,角速度扰动耦合有所不同。为简化分析,认为陀螺为理想的测速环节且陀螺只测量被稳定轴向角速度。

2.1 捷联稳定载体运动

捷联稳定方式下平台负载通过码盘等相对测量装置闭环在载体上,陀螺安装在载体上,敏感载体角速度ωbz,并以指令的形式发给控制器,结构图如图 4所示。其中,F(s)为控制器传递函数,ωi为跟踪指令角速度。ωbz由于闭环的作用会按 1∶1的方式传递到平台上,力矩电机实际控制负载与载体的相对转速 ˙θa=ωaz-ωbz,用以对消载体角速度ωbz。

所以捷联稳定方式下描述载体运动耦合的旋转矩阵为所以捷联稳定方式下载体角速度耦合模型为

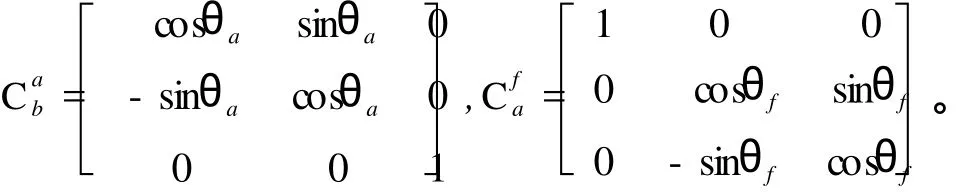
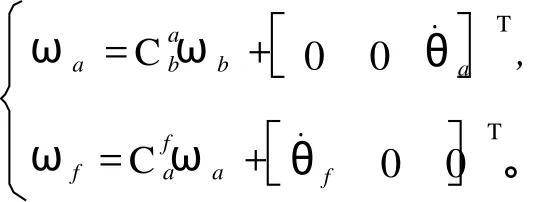
图 4 捷联稳定方式载体角速度传递框图

Fig.4 Coupling of basement rotational speed at strapdown stabilization

2.2 直接稳定载体运动

直接稳定方式情况下陀螺安装在平台负载上,平台通过陀螺闭环于惯性空间如图 5所示,此时电机更是驱动负载相对惯性空间运动。

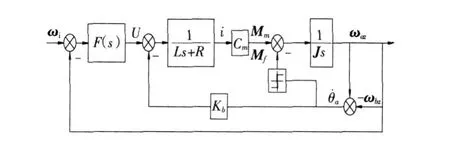
图 5 直接稳定方式载体角速度传递框图Fig.5 Coupl ing of basement rotational speed at direct drive stabilization

由于闭环的作用,ωbz对平台的影响较小,而力矩电机实际控制的是负载相对惯性空间转速,根本不存在 1∶1的传递,也根本不存在驱动框架转角速度对消,此时仅仅为一效果量。

直接稳定方式中常用的是一种速度双环串级控制结构的稳定方式[2,6],为通过测速机或者码盘测量载体与负载相对速度构成速率内环,通过陀螺测量平台相对惯性空间速度构成速率外环,内环隔离摩擦扰动,外环隔离载体扰动,其框图如图 6所示。

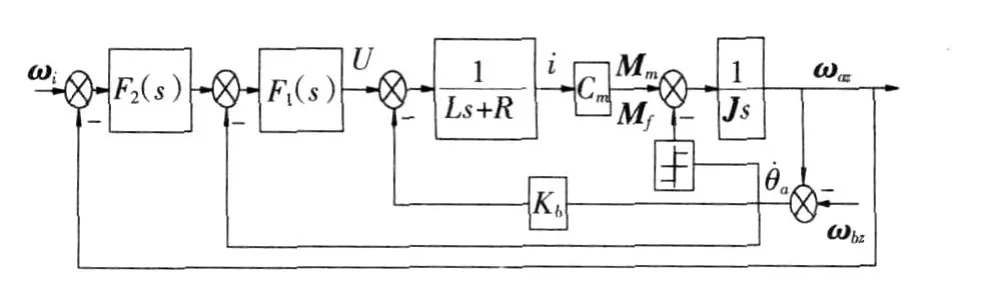
图6 双闭环稳定角速度传递框图Fig.6 Coupling of basement rotational speed at double closed loop stabilization

这种稳定方式的实质仍然是直接稳定,但不同频率段略有不同:双环系统内环带宽一般比外环宽,那么外环带宽以内,体现直接稳定方式的特性,力矩电机驱动平台相对惯性空间运动;外环带宽以外,内环带宽以内,体现捷联稳定特性,力矩电机驱动平台相对载体运动。通过设计合理带宽设计,使得外环低频段大于等于载体扰动ωbz的频率,那么ωbz影响被外环有效隔离,这种速度双环串级控制结构实际上等效于直接稳定方式,电机直接驱动负载相对惯性空间转动,即不存在载体扰动的 1∶1传递。

所以直接稳定方式下描述载体运动耦合的旋转矩阵为

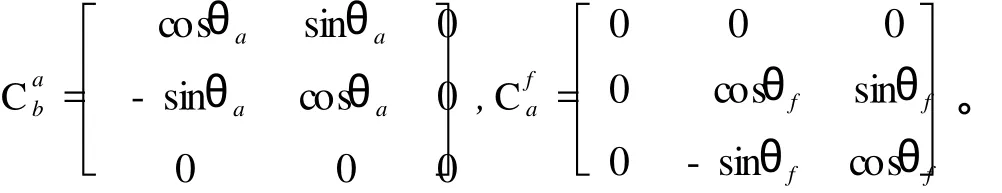
所以直接稳定方式下载体角速度耦合模型为

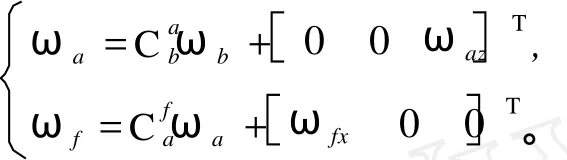
至于ωaz、ωfx如何变化应反映在动力学模型中,与载体角速度耦合模型没有关系。

3 结 论

(1)直接带动耦合包含反电动势耦合、摩擦约束耦合及通过传动装置 (直接驱动)情况下为刚性连接三种作用,但是摩擦约束耦合并不时时对载体运动传递起推动作用,有时起阻碍作用,有时没有作用。

(2)捷联稳定方式与直接稳定方式下载体运动传递的机制不同:直接稳定方式下载体运动角速度不存在1∶1传递,其运动模型的旋转矩阵中相应元素宜写为 0;捷联稳定方式下载体运动角速度存在1∶1传递,其运动模型的旋转矩阵中相应元素宜写为 1。按载体运动耦合的实际情况分开建立了直接稳定方式与捷联稳定方式下的角速度耦合模型。

[1] 郭富强,于 波,汪叔华.陀螺稳定装置及其应用[M].西安:西北工业大学出版社,1995.

[2] 王连明.机载光电平台的稳定与跟踪伺服控制技术研究[D].长春:中国科学院长春光学精密机械与物理研究所,2002.

[3] 胡浩军,毛 耀,马佳光,等.稳定平台对基座角速率扰动的抑制能力[J].电机与控制学报,2007,11(1):25-28.

[4] 秦永元.惯性导航[M].北京:科学出版社,2006.

[5] 范大鹏,张智永,范世珣,等.光电稳定跟踪装置的稳定机理分析研究[J].光学精密工程,2006,14(4):673-680.

[6] 姬 伟,李 奇,杨 浦.陀螺惯性平台视轴稳定双速度环串级控制的研究[J].仪器仪表学报,2007,28(1):114-119.

Description of E-O stabilizing and tracking platfor m carriermoving coupling

LI Zhongqin1,DONG Hao2
(1.College of Electric&Information Engineering,Heilongjiang Institute of Science&Technology,Harbin 150027,China; 2.Control&Simulation Center,Harbin Institute of Technology,Harbin 150080,China)

Aimed at addressing the insufficient knowledge of carrier moving coupling description and the failure of the mathematicalmodel of carrier angular velocity coupling to reflect the principle of angular velocity transference,this paper presents an analysis of the change of friction torque and electromagneti sm torque with carrier rotation through theoreticalmodeling,and the principle of angular velocity transference under closed loop control action.The paper stresses that there occurs 1∶1 transference from carrier angular velocity to the platfo rm under strapdown stabilized platfo rm while there is no 1∶1 transference under direct stabilized platfo rm.The paper features the carriermovement angular velocity coupling mathematicalmodel with rotationmatrix elementof 1 on strapdown stabilized platfo rm and of 0 on direct stabilized platfo rm.The results provide theoretical basis for effective isolation scheme of carrier angularmotion.

coupling principles;rotation velocity tran smission;friction moment coupling;direct drive coupling

TP273

A

1671-0118(2011)02-0116-05

2011-02-17

李忠勤(1980-),男,内蒙古赤峰人,讲师,硕士,研究方向:智能控制、数字图像处理等,E-mail:lizhongqin2008@qq.com。

(编辑王 冬)