选煤厂配煤调度中的云模型改进遗传算法
范大鹏, 王雪丹, 李 丹
(1.黑龙江科技学院 计算机与信息工程学院,哈尔滨 150027; 2.黑龙江科技学院 电气与信息工程学院,哈尔滨 150027)
选煤厂配煤调度中的云模型改进遗传算法
范大鹏1, 王雪丹2, 李 丹1
(1.黑龙江科技学院 计算机与信息工程学院,哈尔滨 150027; 2.黑龙江科技学院 电气与信息工程学院,哈尔滨 150027)
针对传统遗传算法求解最优值存在搜索速度慢、容易陷入局部最优解的问题,基于传统遗传算法和云模型,提出了云自适应遗传算法和云遗传算法,建立了选煤厂三产品配煤调度模型,并分别采用改进算法和传统遗传算法求解。实例表明,两种改进算法优于传统遗传算法,为选煤厂配煤调度优化提供了技术途径。
云模型;云自适应遗传算法;云遗传算法;配煤调度
0 引 言
基本遗传算法(GA)和自适应遗传算法存在搜索速度慢、容易局部陷入最优解等问题。遗传算法的操作规则是概率性而非确定性的。当传统遗传算法交叉变异操作以一定概率执行后,交叉点和变异位随机变化,所生成的下一代个体也随机变化,所以其进化的方向是随机的、不可控的和无记忆的。实数编码虽然很大程度上解决了 GA算法精度和存储量的问题,但其作为主要交叉算子的算术交叉都为凸运算[1],使整个群体寻找最优受到了限制,并有未成熟收敛于局部最优的可能,而且同样没有解决进化方向的无记忆和随机性问题。
云模型的概念是著名学者李德毅院士提出的。笔者在分析传统遗传算法的基础上,利用云模型的定性与定量间的转换方法,提出了云自适应遗传算法和云遗传算法,并将其应用于选煤厂配煤调度中。
1 传统遗传算法
1.1 基本遗传算法
基本遗传算法[1]可以表示为
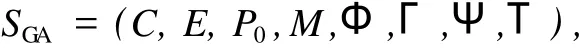
其中,C为个体的编码方法,E为个体适应度评价函数,P0为初始种群,M为种群大小,Φ为选择算子,Γ为交叉算子,Ψ为变异算子,T为遗传运算终止条件。其流程如图1所示。
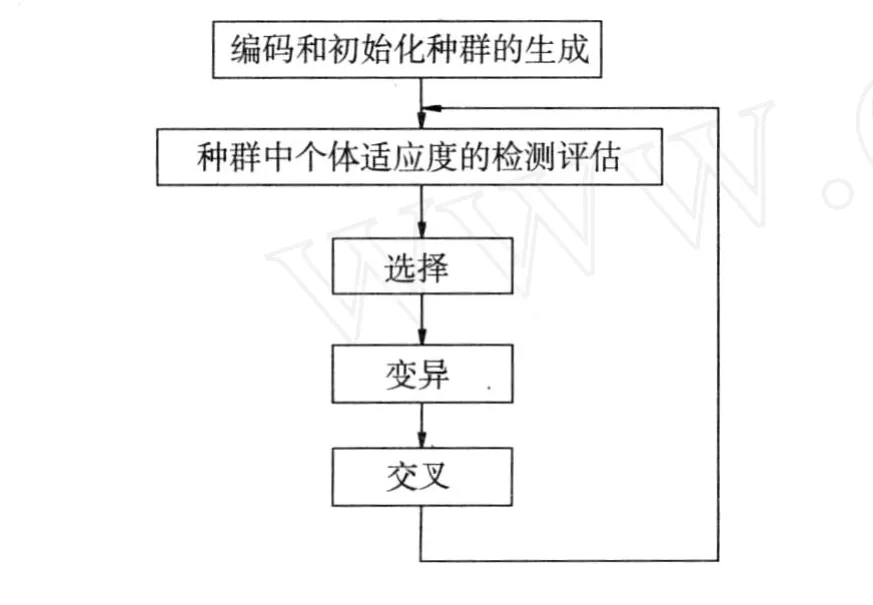
图1 基本遗传算法流程Fig.1 Flow chart of GA

1.2 自适应遗传算法
自适应遗传算法是指具有比例复制、自适应交叉和变异操作的遗传算法,与一般遗传算法相比,它能够较好解决早熟和停滞的问题。
该算法中的交叉Pc和变异Pm可表示为[1]:
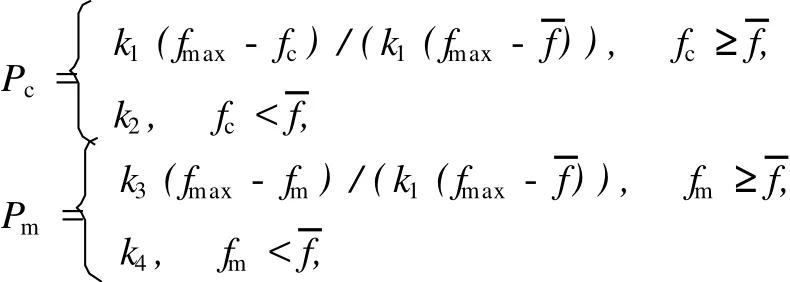

2 改进遗传算法
2.1 云模型
设U是一个用精确数值表示的定量论域,X⊆U,T是U空间上的定性概念,若元素x(x∈X)对T所表达的定性概念的隶属确定度CT(x)(CT(x)∈[0,1])是一有稳定倾向的随机数,则概念T从论域U到区间[0,1]的映射在数域空间的分布称为云(Cloud)。CT(x)在[0,1]上取值,故云是从论域到区间[0,1]的映射,即
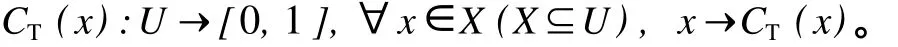
从云的基本定义可以看出,论域中某一元素与它对T的隶属度之间的映射是一对多的关系,而不是传统模糊隶属函数中的一对一的关系[2]。
云模型包括正态云、X条件云、Y条件云三种。
云模型具有稳定性和随机性,笔者根据这一特点,基于基本遗传算法和自适应遗传算法,提出了云自适应遗传算法和云遗传算法。
2.2 云自适应遗传算法
云自适应遗传算法[3]过程如下:
(1)初始化种群。
(2)计算适应度。
(3)选择操作。
(4)交叉。具体步骤为:
a 计算父母染色体适应值、种群规模的平均适应值 ave-f;
b 选取父母染色体大的适应值f;
c 当f小于 ave-f,选Pc为大概率交叉概率k3值,k3为[0,1]区间的数据;
d 当f大于 ave-f,Pc由云发生器产生,云发生器是以平均适应度为期望值,以适应度最大值减去平均适应度为熵和超熵产生的云模型图,云图的确定度μ是[0,l]区间的随机数,即要选取的交叉概率Pc。
(5)变异。具体步骤为:
a 计算当前染色体适应值f、种群规模的平均适应值 ave-f;
b 当f小于 ave-f,选Pm为大概率交叉概率k4值,k4为[0,1]区间的数据;
c 当f大于 ave-f,Pm由云发生器产生,云图的确定度μ是[0,l]区间的随机数,即要选取的交叉概率Pm;
d 随机产生变异点,采用单点变异,新个体复制到选择个体中,保留最优个体。
(6)将新种群复制到原种群,判定终止条件是否达到,若达到则转到步骤(7),否则转到步骤(2)。
(7)输出结果。
2.3 云遗传算法
云遗传算法(CGA)描述如下:
(1)初始化种群。
(2)计算适应度。
(3)选择操作。
(4)交叉。具体步骤为:

数Temp,当μ>Temp时,更新个体。
(6)转步骤(2),直到满足停止条件。
xf和xm分别为交叉操作的父个体和母个体,Ff和Fm则分别对应它们的适应度。F′为交叉父个体的最大值,意味着交叉操作中的Ex由父母双方按适应度大小加权确定,并向适应度大的一方靠近。c1、c2、c3、c4为控制系数。
显然,交叉操作实现了染色体(个体)的整体进化,而变异操作则反映染色体中某个基因在一定范围内的突变。CGA不再引入交叉和变异概率。
3 选煤厂配煤调度模型
3.1 三产品配煤模型
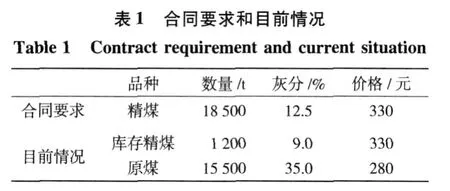
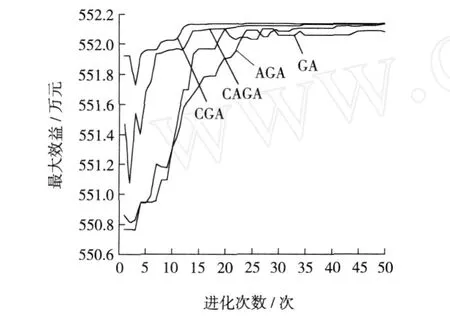
设三种参配产品的灰分、百分率分别为K1、K2、K3、X1、X2、X3,X1+X2+X3=1;目标产品灰分为K,满足Kmin 目标产品与参配产品存在如下关系: 可以看出,该问题为一定约束条件下的目标函数优化问题。设三种参配产品的生产成本分别为C1、C2、C3,则配煤的目标应为追求成本F(x)最低,即 其约束条件为: 对于上述线性规划模型,需根据约束条件和目标函数求解百分率,即求X1、X2和X3。 假设选煤厂洗选各种煤所消耗的吨原煤单位时间成本是近似相同的,调度模型就可转化为求一组合适的Km、Bk,使其经济效益最大。这是带有约束的数学规划问题,目标函数[4-5]为 其中,Km为实际生产精煤的灰分,Ke为单日计划(合同)要求的精煤灰分,K0为原煤的灰分,We为日计划目标精煤的产量,Wm为库存精煤量,W0为用来和实际生产的精煤配煤的原煤量,P为合同要求的精煤的价格,P0为原煤价格,Pb为中煤和煤泥的价格,Cm为洗煤时单位时间生产成本,Φ(K0,Km)为精煤的产率函数,V(K0,Ke)为洗煤厂的分选速度函数,Γ(K0,Ke)为中煤和煤泥的产率函数。 目标函数的约束条件为: 其中,Kk为库存精煤的灰分,Wk为实际生产精煤量,Bk为库存精煤用来配煤的百分比。 (2)运输工具(火车)到达时,应完成选煤过程,且 其中,Ttrain为运输工具到达时间。 (3)根据现实情况,还应有边界条件,如 0≤Bk≤1,K0≥Ke,K0≥Km,K0≥Kk。 以南屯选煤厂为例[6],合同要求和目前生产情况如表1所示。 该厂单位时间生产成本为 43元,基本处理速度为 1 500 t/h,中煤和煤泥的价格为 290元/t。已知 GA算法中交叉数值为 0.25,变异数值为 0.05,种群个数为 50个,分别采用基本遗传算法(GA)、云遗传算法(CGA)、自适应遗传算法(AGA)、云自适应遗传算法(CAGA)进行仿真,如图 2所示。 图2 四种算法的运行结果Fig.2 Run results of four algorithm s 从图 2可以看出,基本遗传算法的运行时间最长,云遗传算法运行时间最短,云自适应遗传算法和云遗传算法的运行时间均少于基本遗传算法和自适应遗传算法。从运行结果来看,云遗传算法运行结果精度最高,基本遗传算法运行结果精度最低。综上,改进的遗传算法优于传统遗传算法。 根据基本遗传算法、自适应遗传算法及云模型理论,提出云自适应遗传算法和云遗传算法。前者保留了交叉概率和变异概率,而后者去掉了交叉概率和变异概率。将两种改进算法应用于选煤厂配煤调度优化中,并与传统算法进行比较。结果表明,两种改进的遗传算法均优于传统遗传算法,具有应用价值。该研究为选煤厂配煤调度优化提供了更好的途径。 [1] 雷英杰,张善文,李续武,等.遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005. [2] 李德毅,杜 鹢.不确定性人工智能[M].北京:国防工业出版社,2005. [3] 戴朝华,朱云芳,陈维荣,等.云遗传算法及其应用[J].电子学报,2007,35(7):1 419-1 424. [4] 高 莉,于洪珍,王艳芬.基于多传感器信息融合的选煤厂配煤调度[J].中国矿业大学学报,2004,33(1):100-102. [5] 郭西进.选煤厂 C IMS环境下管理信息系统的分析、设计、应用[M].徐州:中国矿业大学出版社,2003. [6] 路迈西.选煤厂技术管理 [M].徐州:中国矿业大学出版社,2005. [7] 刘立民,潘 伟,庞彦军,等.多阶段复合型遗传算法的结构及性能研究[J].河北工程大学学报:自然科学版,2010(2): 107-112. Improved cloud-based genetic algorithm for coal blending scheduling in coalpreparation plant FAN Dapeng1,WANG Xuedan2,L I Dan1 In response to traditional genetic algorithm(GA)suffering from a lower convergent speed and greater tendency to get stuck at a local optimum solution,as is evident in the opt imal value solution, this paper proposes a cloud-based adaptive genetic algorithm(CAGA)and cloud-based genetic algorithm (CGA),based on traditional genetic algorithm and cloud model.The paper offers coal blending schedulingmodel of three productions,as is shown by reference[4]and provides solution by the two improved algorithms and GA respectively.The exper iment confi rms that the two improved algorithms exhibiting advantages over GA,are of application value. cloud model;cloud-based adaptive genetic algorithm;cloud-based genetic algorithm; coal blending scheduling TP301.6;TD928.9 A 1671-0118(2011)02-0112-04 2011-03-14 范大鹏(1979-),男,黑龙江省哈尔滨人,工程师,硕士,研究方向:智能控制、数据融合,E-mail:fandap-02@yahoo.com.cn。 (编辑荀海鑫)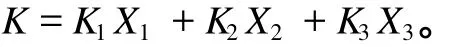
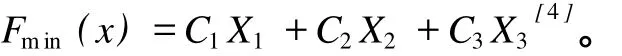
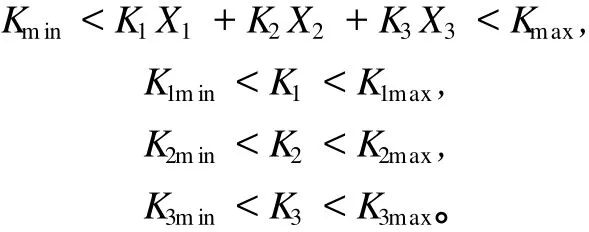
3.2 调度模型
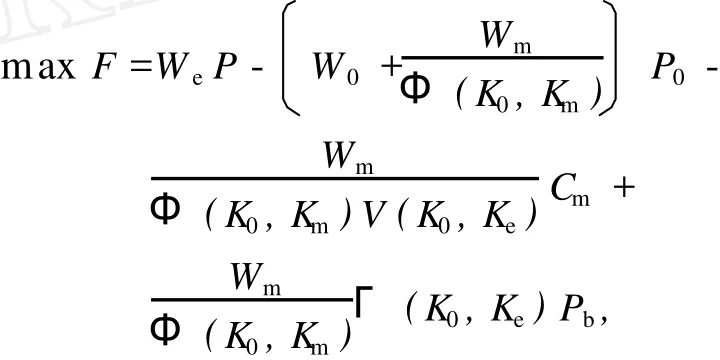
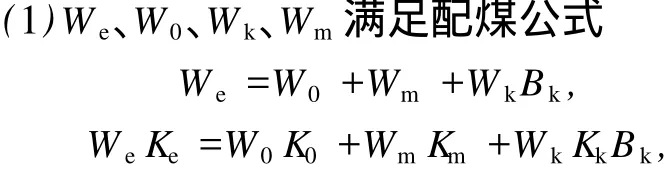
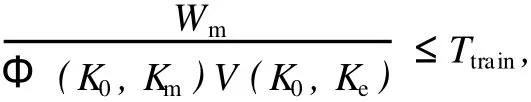
4 实 例
5 结束语
(1.College of Computer&Infor mation Engineering,Heilongjiang Institute of Science&Technology,Harbin 150027,China; 2.College of Electric&Infor mation Engineering,Heilongjiang Institute of Science&Technology,Harbin 150027,China)

