考虑焊缝尺寸的 T型相贯节点极限承载力计算

夏新强, 侯智超, 刘小蔚

(中国矿业大学 力学与建筑工程学院,江苏 徐州 221116)

考虑焊缝尺寸的 T型相贯节点极限承载力计算

夏新强, 侯智超, 刘小蔚

(中国矿业大学 力学与建筑工程学院,江苏 徐州 221116)

针对屈服线模型计算管结构节点的极限承载力偏于保守的情况,考虑焊缝尺寸的影响,修正了 T型相贯节点极限承载力计算公式,并借助有限元软件进行对比。结果表明,C IDECT公式计算结果偏于保守,修正公式计算结果与有限元计算结果吻合较好,修正公式合理。

T型节点;极限承载力;焊缝尺寸;屈服线模型

0 引 言

管截面在受压、受扭及受弯情况下仍能表现出良好的结构性能,因此,广泛应用于房屋、桥梁及特种结构等领域。管结构节点强度是影响管截面性能的重要因素之一。20世纪 50年代以来,国内外学者对管结构节点的极限承载力计算问题进行了大量的研究工作,提出了多种设计公式及标准。丹麦研究者Johansen提出的屈服线破坏模型广泛应用于主管表面塑性失效的方钢管节点中[1]。由于研究者在简化该模型时,往往忽略焊缝尺寸、圆角效应、局部应变硬化及张力场效应等因素的影响,致使公式的计算结果偏于保守[2-4]。为解决这一问题,笔者考虑焊缝的尺寸效应,修正了常见的 T型方钢管节点极限承载力计算公式,并借助有限元软件进行对比。

1 修正公式

图1为 T型方钢管相贯节点的外形尺寸。为方便研究,采用较为简化的屈服线模型,如图 2所示。

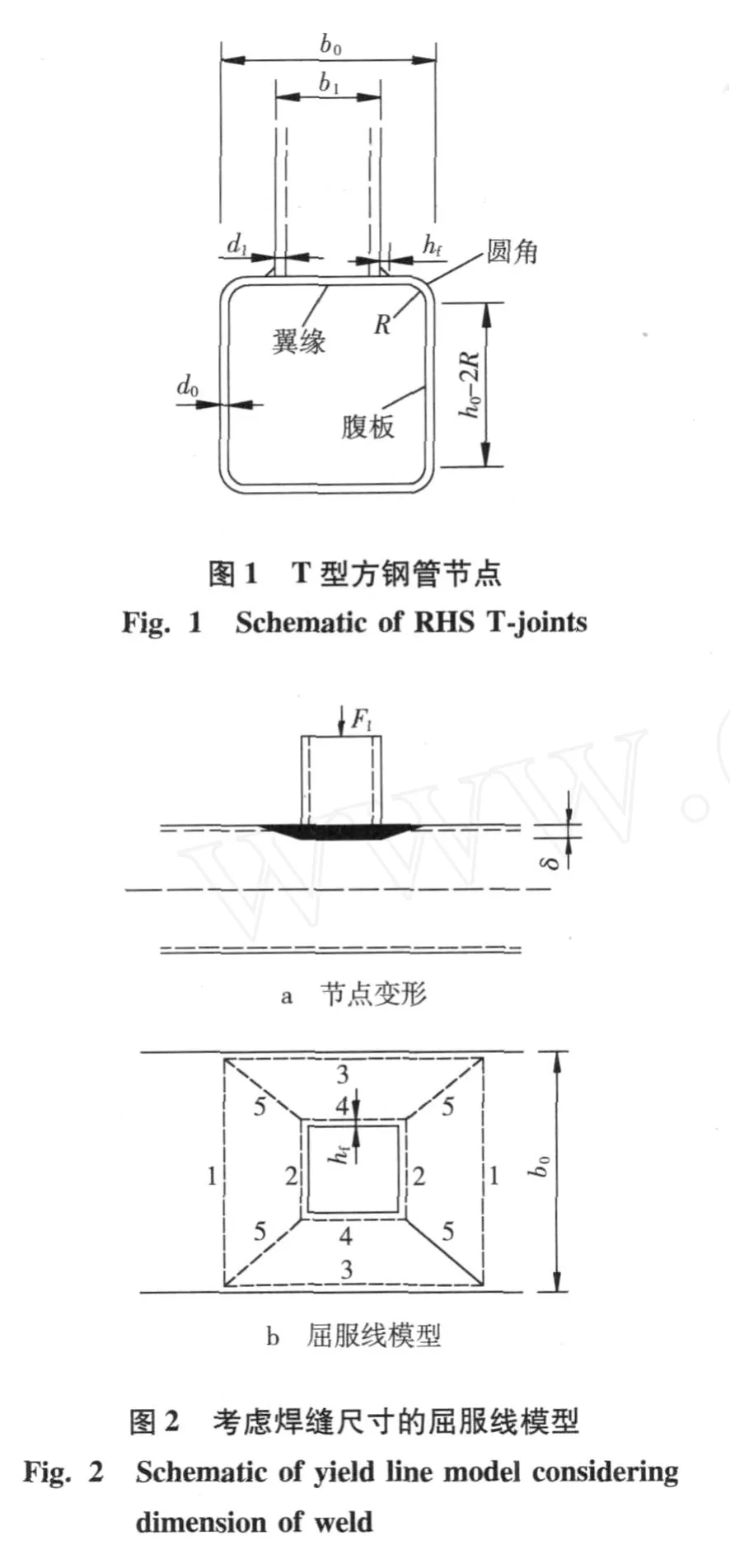
根据屈服线方法原理,支管轴向荷载F1对于位移δ所做的外力功与具有塑性线长度li和转角 φi的塑性铰系统的内能相等,即

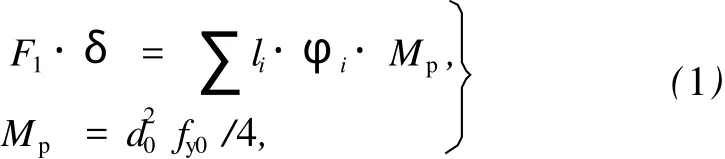
式中:Mp——截面单位长度上的塑性极限弯矩;

d0——主管厚度;

fy0——钢材屈服强度。

已知主管宽度b0、支管宽度b1、焊缝的焊脚高度hf,令β=b1/b0,γ=b0/2d0,ω=2hf/b0,计算图 2中各屈服线所消耗的内能,结果如下:

屈服线1

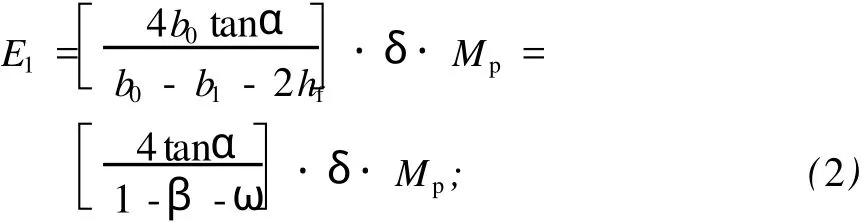
2 有限元模型

根据 GB/T 6728—2002,选取 6个 T型节点用于ANSYS有限元计算。节点截面尺寸及主要几何参数见表 1,其中n为截面圆角的倒角系数。节点材料采用我国常用的Q345,其弹性模量为 210 GPa,泊松比为 0.3。假定其本构关系为理想弹塑性并符合Von Mises屈服准则,且不考虑焊接残余应力的影响。管件及焊缝均采用 Shell 181单元,建模时将壳单元的节点偏置到顶面,从而使焊缝壳单元更接近实际情况 (图 3)。网格划分的单元形状为四边形,考虑到相贯线附近区域的应力梯度较大,进行了较密的划分(图 4)。为了避免边界条件影响节点性能,主管长度取主管宽度的 6倍,支管长度取支管宽度的 5倍[5-7]。计算模型中,主管管端除轴向自由度以外,其他所有自由度均施加约束,支管管端自由。

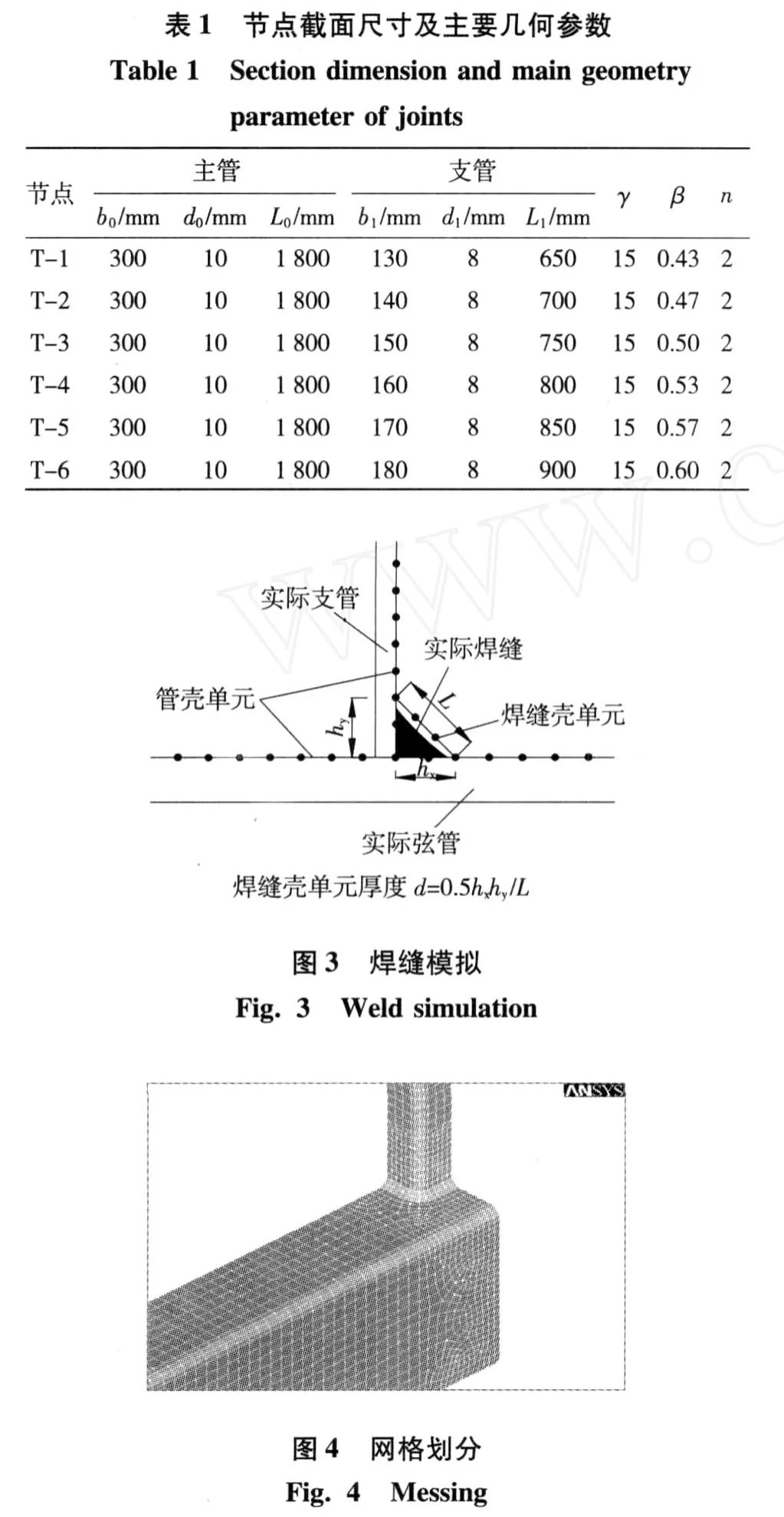
根据欧洲规范,角焊缝的焊脚高度hf必须满足:当fy>345 MPa时,hf>1.05 t。根据我国钢结构规范,管结构中角焊缝的焊脚尺寸hf不宜大于支管壁厚度的 2倍。综合考虑,焊脚高度取支管壁厚度的1.5倍,焊缝壳单元的厚度取焊脚高度的 0.707倍。

3 结果分析

不同β值的方钢管相贯节点在支管轴向力F作用下的荷载 -位移曲线如图 5所示。从图 5中可以看出,虽然节点产生了较大的凹陷变形,但由于主管张力场效应的影响,节点依旧可以承载,且承载力呈现缓慢增大的趋势。以极限变形准则为极限承载力的判定准则,即主管表面凹陷值达到 0.03b0时的荷载为节点的极限承载力[8]。由图 5也可见,随着β值的增大,节点的极限承载力也在不断增加,节点极限变形δmax为 9 mm。

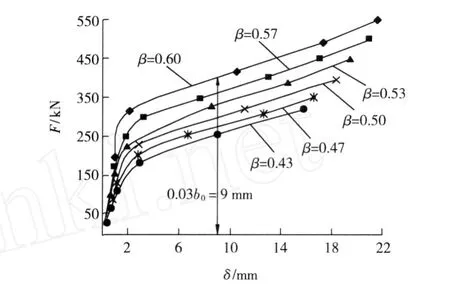
图 5 不同β对应的节点荷载 -位移曲线Fig.5 Load-displacement curves of joint under different values ofβ

图 6给出了根据有限元模型、C IDECT(国际管结构发展与研究委员会)设计指南和修正公式 (10)计算得到的节点极限承载力。

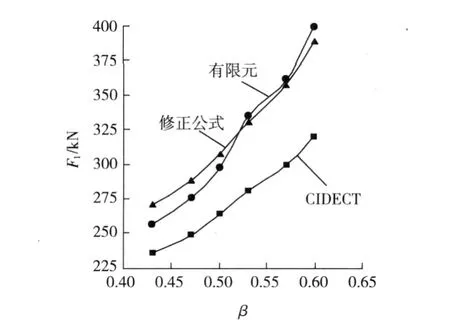
图6 不同计算方法的节点极限承载力Fig.6 Ult imate capacity of jo ints calculated by differentmethods

从图中可以看出,修正公式的计算结果与有限元计算结果的最大误差为 5.9%,平均误差为3.02%,两者吻合较好;而 C IDECT设计指南计算结果与有限元计算结果偏差较大,最大误差达到19.8%,平均误差为 13.7%,C IDECT设计指南给出的设计公式偏于保守。由此可见,考虑焊缝尺寸影响的修正公式能够较为合理的估算 T型相贯节点的静力极限承载力。

4 结束语

为解决屈服线模型计算管结构节点的极限承载力偏于保守的问题,笔者考虑焊缝尺寸的影响,修正了 T型相贯节点极限承载力的计算公式。对比结果显示,采用修正公式计算的极限承载力比 CIDECT公式计算的更接近有限元计算结果。C IDECT计算结果偏于保守,而考虑焊缝尺寸影响的修正公式可合理估算 T型相贯节点的极限承载力。该研究可为管结构节点极限承载力计算方法的深入研究提供参考。

[1] WARDEN IER J.钢管截面的结构应用[M].张其林,刘大康,译.上海:同济大学出版社,2004:84-89.

[2] 景明勇,王元清,边振义,等.空间钢管结构 TT型及其加强节点的承载性能分析[J].四川建筑科学研究,2007,33(6): 51-54.

[3] 丁北斗,吕恒林,周淑春,等.T形圆管相贯节点的抗弯性能试验与理论分析[J].四川建筑科学研究,2008,34(6):16-18.

[4] 孙 鹏,王元清,石永久.考虑倒角系数的 T型铸钢节点轴向承载力非线性分析[J].空间结构,2006,12(2):40-43.

[5] 方敏勇.方管平面 X型和空间 XX型相贯节点的理论和试验研究[D].西安:西安建筑科技大学,2004.

[6] 徐 丹.空间 TT形方管节点静力工作性能的有限元分析[D].武汉:武汉大学,2005.

[7] 陈 鹏.轴向力作用下 T型方管节点滞回性能的试验研究[D].哈尔滨:哈尔滨工业大学,2007.

[8] ZHAO XI AOL ING.Deformation limit and ultimate strength ofwelded T-joints in cold-for med RHS sections[J].JournalofConstructional Steel Research,2000,53(2):149-165.

Calculation of ult imate capacity of RHS-connection of T-joints considering weld d imension

XIA X inqiang,HOU Zhichao,LIU Xiaowei
(School ofMechanics&Civil Engineering,China University ofMining&Technology,Xuzhou 221116,China)

A imed at an alternative to the yield line modelmore likely to give a conservative calculation of ultimate bearing capacity of pipe structure joints,this paper discusses the modification of the calculation formula of ultimate capacity of T-joints,as dictated by the consideration of the influence of weld dimension,and the use of the finite element software for comparison.The results show that C I DECT formula tends to give a more conservative calculation while FEM gives the calculated values closer to the values derived from the modified formula,and the modified formula proves reasonable.

T-joints;ultimate capacity;d imension ofweld;yield line model

TU392.3

A

1671-0118(2011)02-0153-04

2011-01-17

夏新强(1986-),男,江苏省徐州人,硕士,研究方向:钢结构,E-mail:xiaxqiang@126.com。

(编辑荀海鑫)