一类高阶混合中立型微分方程的振动性*
韩忠月
(德州学院数学系,山东德州 253023)
一类高阶混合中立型微分方程的振动性*
韩忠月
(德州学院数学系,山东德州 253023)
研究了一类高阶混合中立型微分方程,得到方程若干新的振动准则,改进和推广了已有的一些结果.
微分方程;高阶;混合中立型;振动性
引言
考虑高阶混合中立型微分方程:
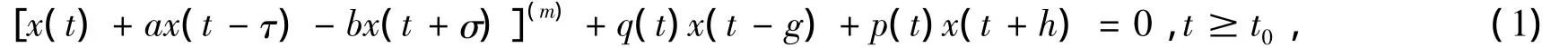
其中 a,b,τ,σ,g,h 为正常数,p,q∈C(R+,R+),m≥1 为整数.
最近,文献[1]研究了奇数阶混合中立型微分方程

解的振动性,其中 c,c*,p,q,g,g*,h,h*是实常数.
中立型泛函微分方程解的渐近性和振动性问题在理论和应用两方面均有重要意义.近三十年来,在这一领域已取得了丰硕成果.在理论方面,最近的研究可参阅文献[1~5]及其引文.当n=1时,方程出现在高速计算机无损传输线路的网络设计中[6,7].当n=2时,方程出现在与弹性棒相连接的振动物体的研究中[8].本文的目的是建立当m为奇数或偶数时,方程(1)新的振动准则,它不仅适用于奇数,而且也能应用于偶数阶.其结果推广和改进了文献[1]中的若干结果.
定义1 函数x(t)∈C[t0,∞)是方程(1)的振动解,如果对每一个正数r皆存在正数t1∈[r,∞),使得x(t1)=0.
1 主要结论
定理1 假设h>σ,g>τ,且m≥3为奇数,如果满足:
(H1)p(t)=p(t-τ)=p(t+σ),q(t)=q(t-τ)=q(t+σ),t∈[t0,∞);
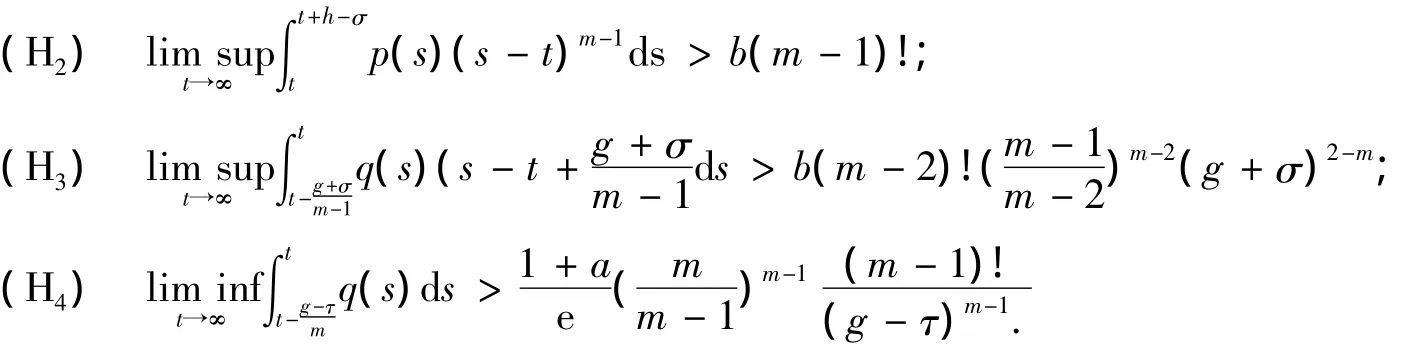
则方程(1)的每一个解是振动的.
证明 假设方程(1)存在非振动解,不是一般性,我们可以假设存在t1∈[t0,∞),使得x(t)>0,x(t- τ)> 0,x(t- g)> 0,t > t1.令
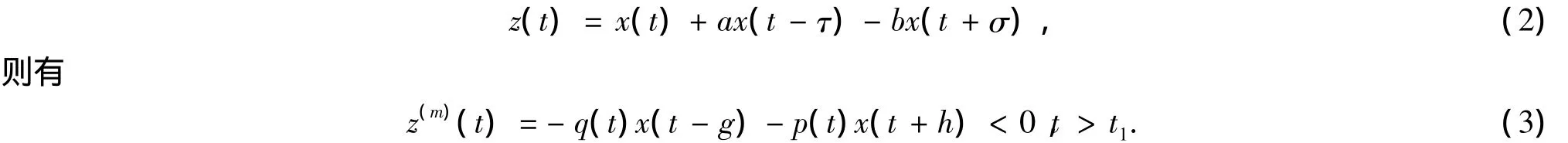
显然z(i)(t),i=0,1,2,…,m -1最终同号,因此只有两种可能的情况:

首先考虑情况(a)成立,即z(t)<0,t≥t2≥t1.令

结合式(2)和式(4)可得
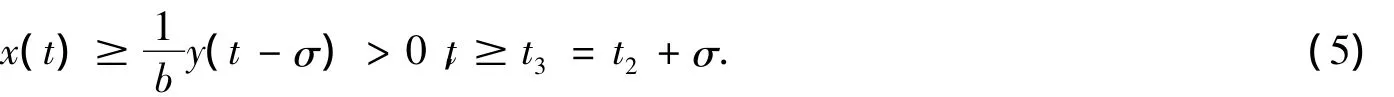
联立式(3),式(4)和式(5)可以得到
由于z(i)(t),i=0,1,2,…,m -1最终同号,再应用文献[7]引理5.2.2,总有y(t)> 0,y'(t)> 0,y(m)(t)> 0最终成立,且只能有以下两种可能:
(ⅰ)y(t)> 0,y'(t)> 0,y(m-1)(t)> 0,y(m)(t)> 0, t≥ t4≥ t3;
(ⅱ)y(t)> 0,y'(t)> 0,y(m-1)(t)< 0,y(m)(t)> 0, t≥ t4≥ t3.
如果(ⅰ)成立,应用文献[7]引理5.2.2,则有 y(i)(t)> 0,i=0,1,…,m,t≥ t4.结合等式:
很容易得到
在式(7)中令u=s+h-σ,v=t+h-σ,t4<t<s<t+h-σ,则有
在[t,t+h -σ]上对式(6)积分,并应用式(8)会得到
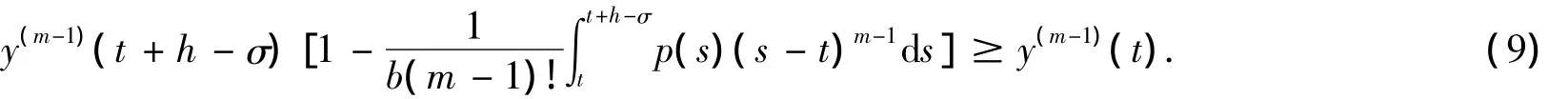
应用条件(H2),式(9)成立只能是y(m-1)(t)为非正的变量,与假设(ⅰ)矛盾.
如果(ⅱ)成立,应用文献[7]引理5.2.2,则有y(m-2)(t)> 0,y(m-2)(t)y(m-1)(t)< 0,t≥t4.联立式(2),式(3),式(4)和式(5)可以得到
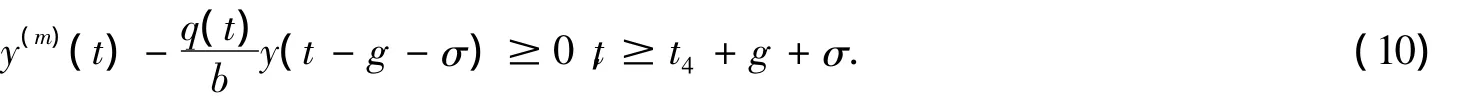
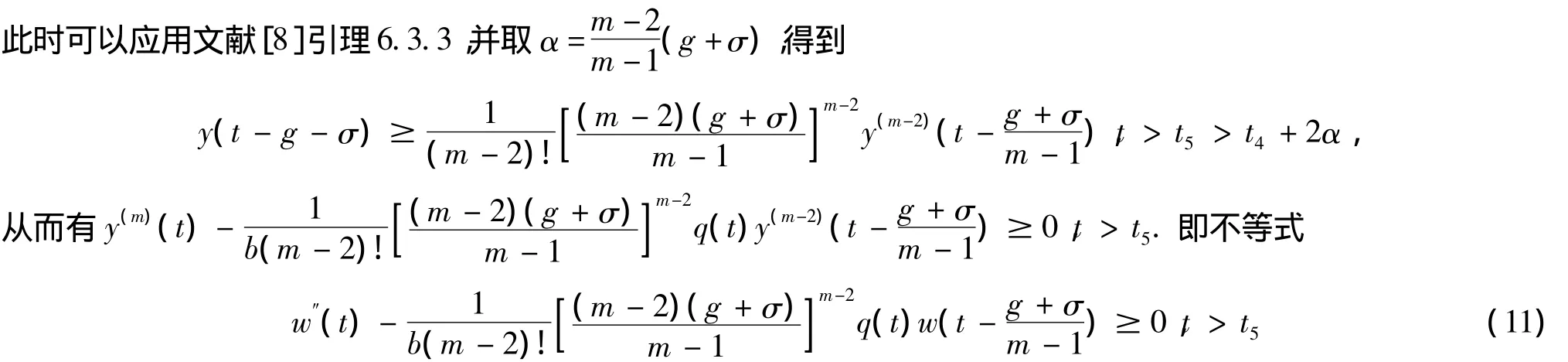
有正解w(t)=y(m-2)(t).根据文献[9]定理2.2.6,结合条件(H3),不等式(11)没有满足w'(t)w(t)<0的最终正解,因此假设的(ⅱ)不成立.总上z(t)<0不成立.
其次考虑情况(b)成立,即z(t)>0,t≥t2≥t1.类似(a)的证明,我们也是采用否定z'(t)>0与z'(t)<0都最终成立的方法来完成情况(b)的证明.令
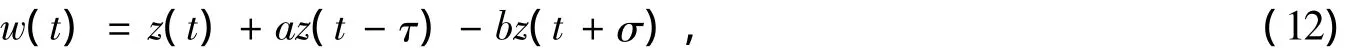
则有
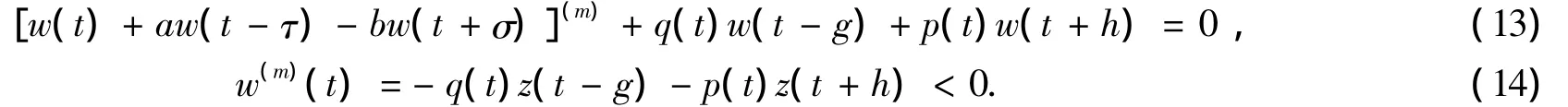
应用文献[7]引理 5.2.1,可得 z(i)(t),i=0,1,2,…,m -1 最终同号,并类似以上证明可以得出 w(t)>0,w(m-1)(t)>0最终成立.
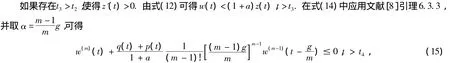
即不等式
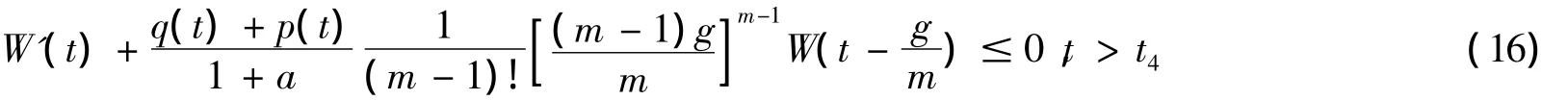
有正解 W=w(m-1)(t).应用文献[9]引理1.4.1,结合条件(H4),不等式(16)不存在最终正解,矛盾.

有正解W=w(m-1)(t).应用文献[9]引理1.4.1,结合条件(H4),不等式(18)不存在最终正解,矛盾.定理1证毕.
根据文献[9]定理2.2.6,不难得到方程(1)振动的另一个判据:
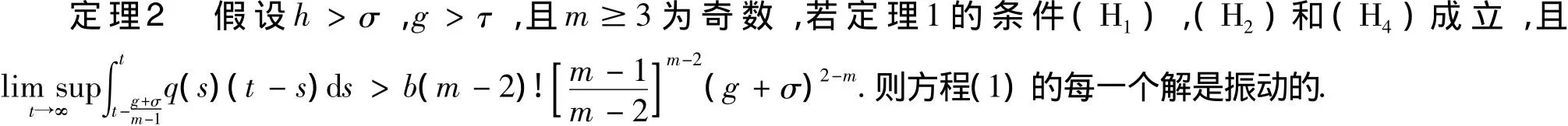
当m=1时,作为奇数阶高阶微分方程的特殊情况,有下列结论:
定理3 当m=1时,若h>σ,g>τ,且定理1的条件(H1)及下列条件成立:
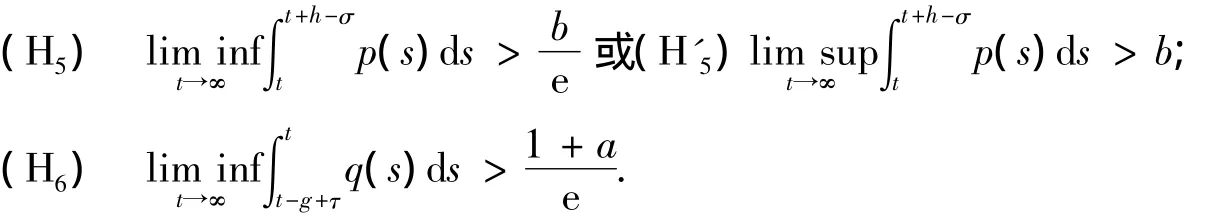
则方程(1)的每一个解是振动的.
作为方程(1)的特殊情况,当p,q∈C(R+,R+)皆为常数序列时,即考虑方程:
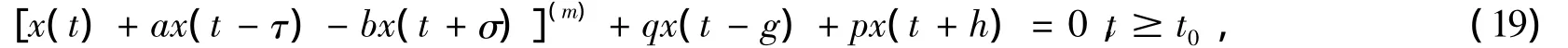
其中m为奇数.有如下结论:
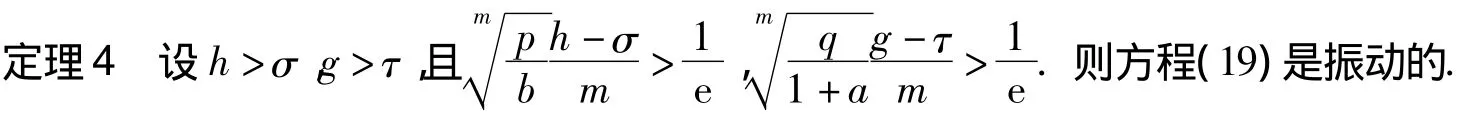
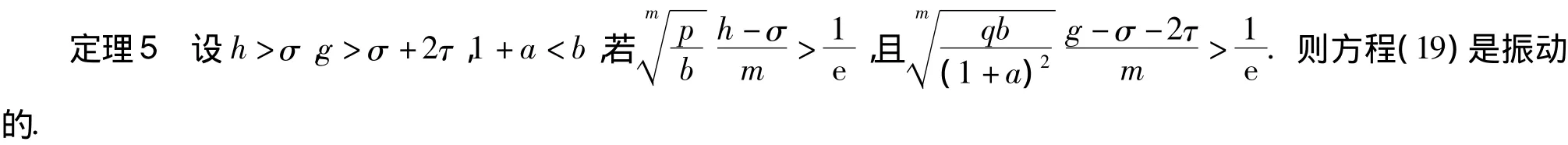
当m为偶数时,可类似得到如下结论:
定理6 假设h>σ,m为偶数且:
(H7)p(t)=p(t- τ)=p(t+ σ),q(t)=q(t- τ)=q(t+ σ),t∈[t0,∞);
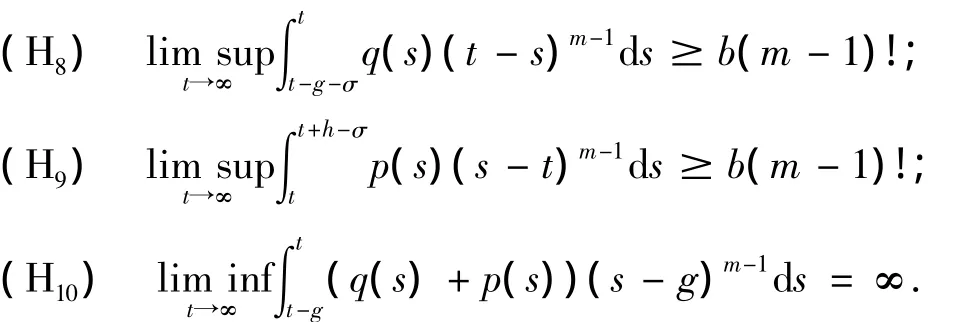
则方程(1)是振动的.
作为方程(1)的特殊情况,当p,q∈C(R+,R+)皆为常数序列时,即考虑方程:
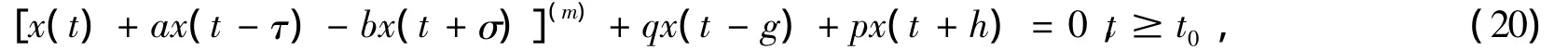
其中m为偶数,有如下结论:
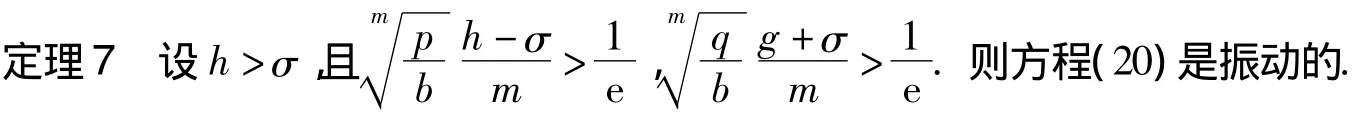
[1]程金发.高阶混合中立型微分方程解的振动性[J].系统科学与数学,2001,21:287-291.
[2]Agarwal R P,Grace S R.Oscillation for certain neutral functional differential equations[J].Comput Math Appl,1999,38:1 -11.
[3]Grace S R.Oscillation criteria for n th -order neutral functional differential equations[J].J Math Anal Appl,1991,184:44 -55.
[4]Tanaka S.Existence of positive solutions of higher order nonlinear neutral differential equations[J].Rocky Mount J Math ,2000,30:1139-1149.
[5]Zafer A.Oscillation criteria for even order neutral differential equations[J].Appl Math Lett,1998,11:21 -25.
[6]Slemrod M,Infante E F.Asymptotic stabilitycriteria for linear systems of difference -differential equations of neutral type and their discrete analogues[J].J Math Anal Appl,1972,38:399 -415.
[7]Ladde G S,Lakshmikantham V,ZHANG Bing-gen.Oscillation theory of differential equations with deviating arguments[M].New York:Marcel Dekker,1987.
[8]Agarwal R P,Bohner M,LI Wan-tong.Nonoscillation and oscillation Theory for Functional Differential Equations[M].New Work:Marcel Dekker,2004.
[9]Agarwal R P,Grace S R,O'regan D.Oscillation theory for second order dynamic equations[M].New York:Taylor Francis,2003.
Oscillatory Behavior for a Class of Higher Order Mixed Neutral Differential Equations
HAN Zhong-yue
(Department of Mathematics,Dezhou University,Dezhou Shandong 253023,China)
In this paper,a class of higher order mixed neutral differential equations is considered.Some new oscillations criteria of the solutions are obtained.The results extend and improve some known results.
differential equations;the higher order;mixed neutral type;oscillation
O 175.1
A
1673-2103(2011)05-0015-04
2011-08-22
德州学院科技类项目(310819)
韩忠月(1963-),女,河北唐山人,教授,研究方向:方程定性理论.

