一类正线性映射的可分解性*

朱 青

(菏泽学院数学系，山东菏泽 274015）

一类正线性映射的可分解性*

朱 青

(菏泽学院数学系，山东菏泽 274015）

定义线性映射φ =φ1⊕φ2:M2(C)⊕M2(C)→M2(C)⊕M2(C)为 φ(A⊕B)=φ1(A)⊕φ2(B)，∀A，B∈M2(C)，其中φi(i=1，2)为M2(C)到M2(C)上的线性映射.证明了正线性映射φ=φ1⊕φ2是可分解的，并给出了co-全正映射的一个充分必要条件.

正线性映射;全正映射;co-全正映射

引言

在量子相关性的分析中，正线性映射的可分解性质对于量子映射的分析至关重要.对于线性映射:φ:Mm(C)→Mn(C)，Størmer和 Woronowicz证明了 m=n=2 或 m=2，n=3 时每个正线性映射都是可分解的［1，2］;Choi及Woronowicz分别在m=n=3及m=2，n=4的情况下给出了不可分解映射的例子［2，3］;对于高阶情况至今未得到解决.本文针对特殊的高阶情况讨论一类正线性映射的可分解性，并给出了co-全正映射的一个充分必要条件，拓展了正线性映射可分解性的研究范围.

1 预备知识

引理1［3］令 φ:Mm(C)→Mn(C)为线性映射，则:

1)φ为正线性映射当且仅当Hφ块正;

2)φ 为全正(co-全正)映射当且仅当Hφ(HTφ)∈Mm(Mn(C))+.

2 主要结果及证明

定义线性映射φ=φ1⊕φ2:M2(C)⊕M2(C)→M2(C)⊕M2(C)为φ(A⊕B)=φ1(A)⊕φ2(B)，∀A，B∈M2(C)，其中φi(i=1，2)为M2(C)到M2(C)上的线性映射，可得到如下结论:正线性映射φ=φ1⊕φ2是可分解的.下面分四部分对此结论进行证明.

1)φ1，φ2为正线性映射

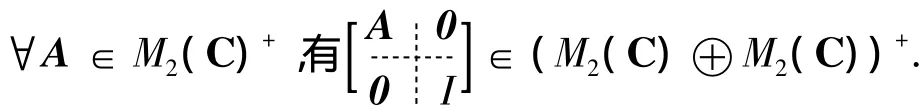
由φ为正线性映射，知:

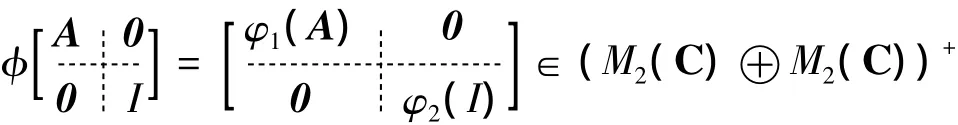
从而φ1(A)∈M2(C)+，故φ1为正线性映射.同理可证φ2为正线性映射.

2)若φ1，φ2为全正映射，则φ为全正映射

对于∀k∈N，

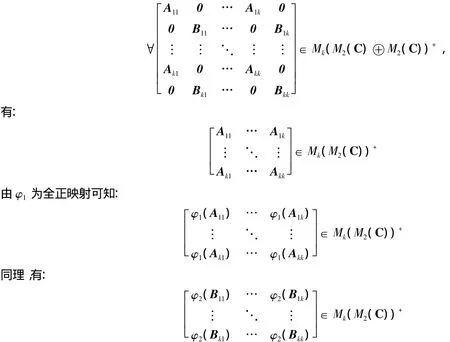
对于任意的2 维向量 ξi，ηj(1≤i，j≤k)有:

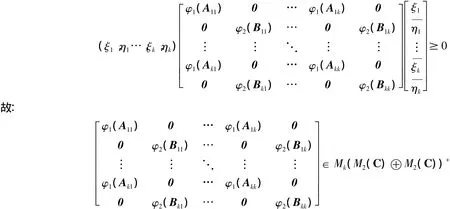
从而φ为全正映射.

3)若φ1，φ2为co-全正映射，则φ为co-全正映射

证明过程类似于2).

4)正线性映射φ=φ1⊕φ2是可分解的

已经知道所有正线性映射φ:M2(C)→M2(C)都是可分解的［1］，故φi(i=1，2)可以写成如下形式:φi=φi1+φi2，其中 φi1为全正映射，φi2为 co-全正映射.从而

则φ=φ1+φ2，由2)，3)知，φ1为全正映射，φ2为co-全正映射.从而φ是可分解的.

证毕.

利用上述方法，可以证明如下两类正线性映射也是可分解的.即:

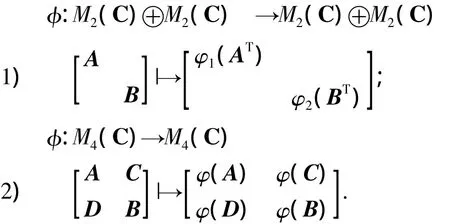
3 总结

本文针对4阶的情况，证明了几类正线性映射是可分解的.从查阅的资料来看，目前对于更高阶的情况尚未有实质性的进展，有待我们继续研究与探讨.

［1］Størmer E.Positive linear maps of operator algebras［J］.Acta Math，1963，110(1):233-278.

［2］Woronowicz S.Positive maps of low dimensional matrix algebras［J］.Rep.Math.Phys，1976，10(2):165-183.

［3］Choi M.Completely positive linear maps on complex matrices［J］.Lin.Alg.Appl，1975，10(3):285-290.

［4］Takesaki M.Theory of operator algebra I［M］.Berlin:Springer-Verlag，2002.

［5］Majewski W A，Marciniak M.On a characterization of positive maps［J］.Phys.A:Math.Gen，2001，34(9):5863-5874.

Decomposable Nature of a Certain Positive Linear Map

ZHU Qing

(Department of Mathematics ，Heze University，Heze Shandong 274015，China)

A linear map φ =φ1⊕φ2:M2(C)⊕M2(C)→M2(C)⊕M2(C)is defined by φ(A⊕B)=φ1(A)⊕φ2(B)for every，A，B∈M2(C)，where φi(i=1，2)is a linear map from M2(C)to M2(C).This paper proves that if φ=φ1⊕φ2is positive，then it is decomposable，and gives one equivalent condition of co-CP maps.

positive linear maps;CP maps;co-CP maps

O 177.1

A

1673-2103(2011)05-0033-03

2011-06-21

菏泽学院研究与发展项目(XY08SX01)

朱青(1982-)，女，山东菏泽人，助教，硕士，研究方向:算子代数.