矩阵的满秩分解及其方法

房月华，陈 萍

（衡水学院 数学与计算机科学学院，河北 衡水 053000)

矩阵的满秩分解及其方法

房月华，陈 萍

（衡水学院 数学与计算机科学学院，河北 衡水 053000)

矩阵的满秩分解是矩阵分解中一类特殊的分解，给出了矩阵满秩分解的 2个定理的证明以及求矩阵满秩分解的 2种方法.

满秩分解；Hermite标准形；初等变换

0 引言

自20世纪50年代以来矩阵的理论和计算方法的研究取得了长足的进展，矩阵理论的应用日益广泛.矩阵已成为人们探索新理论的重要工具，矩阵分解的应用也越来越受到人们的重视.在数值线性代数中，我们常常需要将数域P上的某个已知矩阵写成若干个满足一定条件的特殊类型矩阵之和或矩阵之积的形式，并把这种矩阵表示称为矩阵分解.矩阵分解中有一类特殊的分解，即矩阵的满秩分解，矩阵的满秩分解及其相关行满秩列满秩矩阵的定义和相关性质都有广泛的应用，本文给出了矩阵满秩分解的2种方法及证明.

1 矩阵的满秩分解

定义1[1]设A是秩为r（r＞0)的m×n矩阵，若存在m×r列满秩矩阵F和r×n行满秩矩阵G，使得则称(1)式为矩阵A的满秩分解.

定理1设A为任一秩为r的m×n矩阵，则A必有满秩分解式(1)，其中F为列满秩的，G为行满秩的.

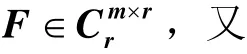
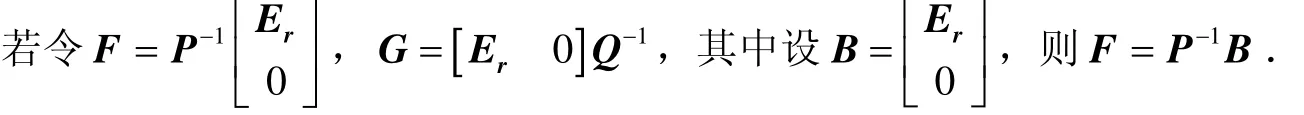
即F为m×r列满秩矩阵，G为r×n行满秩矩阵，且有

故结论成立.

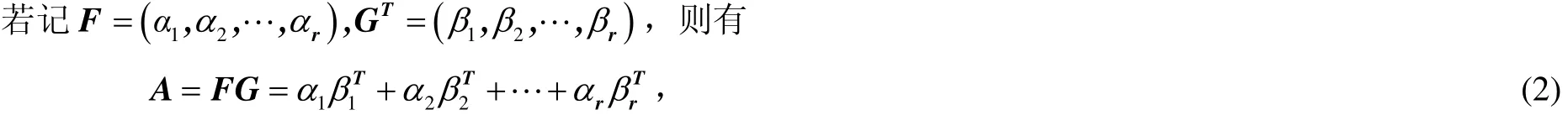
这里，(2)式也是A的满秩分解的一种表示.

定理2设A的秩为r，且A=F1G1=F2G2为矩阵A的两个满秩分解，则

1) 存在r阶的满秩方阵B，使得

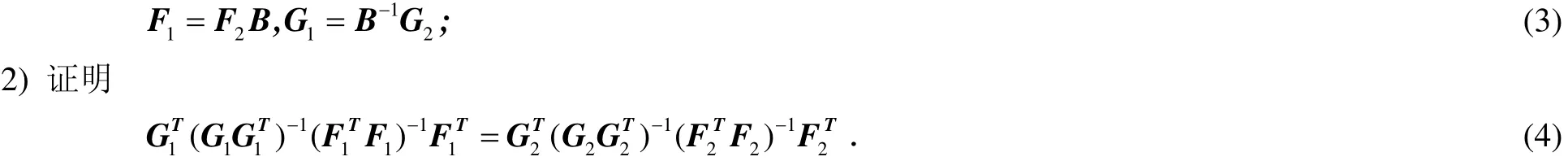
证明1) 因为A有满秩分解F1G1=F2G所以

故G GT与皆为r阶满秩方阵，故由(5)式即知

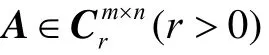
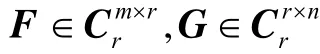
11异矩阵，Q为m×r矩阵，且QH Q=I.于是这里R=R1G，它的r行线性无关.

2 满秩分解的方法

2.1 化为Hermite标准形求满秩分解

定义2[2]设B∈(r＞0)，且满足：

1)B的前r行中每一行至少含一个非零元素，且第一个非零元素是1，而后m−r行元素为零；

2) 若B中第i行的第一个非零元素1在第ji列(i= 1,2,… .r)，则j1＜j2＜…＜jr；

3)B中的j1,j2,… ,jr列为单位矩阵Im的前r列.

那么就称B为Hermite标准形.

有了上述定义我们现在补充定理1的第三种证明方法.

证法3在A的Hermite标准形中取前r行，构成矩阵G，则G是秩为r的r×n矩阵，若令T1=(ei1,ei2,…,eir)，则有GT1=Ir.为确定m×r矩阵F，使得A=FG，将右乘T1得F=AT1，即F由A的第i1,i2,… ,ir列构成.按方法1可证rankF=r；故A有满秩分解.

2.2 利用初等行变换求满秩分解

设A的秩为r，则A有r个线性无关的列向量.不妨设其前r个列向量线性无关，于是其后n−r个列向量必可分别表示为前r个列向量的线性组合.用分块矩阵表示，即为

其中A1为A的前r个列生成的m×r列满秩矩阵，Q为r×(n−r)矩阵，于是

例 设A是非零的实对称矩阵，则A为幂等矩阵的充要条件是存在列满秩矩阵F，使得

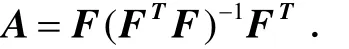
证明当A=F(FT F)−1FT时，易知A2=A；反之，将A做满秩分解得，A=FG.因为AT=A，所以A=FG=GT FT，于是存在非奇异矩阵P，使得GT=FP,A=FPT FT，又因为A2=A，即FPT FT FPT FT=FPT FT，等式两边左乘 (PT)−1(FT F)−1FT，右乘F(FTF)−1，得FTFPT=E，所以PT=(FTF)−1，带入A=F(FT F)−1式，即得A=F(FT F)−1FT，证毕.

3 结论

矩阵的满秩分解是矩阵分解的特殊形式，由于对分解出矩阵的特殊要求，矩阵满秩分解有很好的性质，而它的相关理论的研究也有很重要的意义.因此，在矩阵的相关证明，矩阵满秩分解及相关行满秩列满秩定义都起着十分重要的作用.因此对于矩阵、矩阵的满秩分解及其应用问题还有待于进一步研究.

[1] 程云鹏.矩阵论[M].西安:西北工业大学出版社,2000:220-225.

[2] 史荣昌,魏丰.矩阵分析[M].北京:北京理工大学出版社,2005:183-186.

The Methods of the Full Rank Decomposition of the Matrix

FANG Yue-hua, CHEN Ping
(College of Mathematics and Computer Science, Hengshui University, Hengshui, Hebei 053000, China)

The full rank decomposition of the matrix is a special kind of decomposition in the matrix decomposition. In the article, we give the proof of two theorems of the matrix decomposition; we have got two methods of full rank decomposition of the matrix according to the two theorems.

full rank decomposition; Hermite nomal form; elementary transformation

O151.21

A

1673-2065(2011)04-0016-03

2011-01-10

房月华(1983-),女,河北武强人,衡水学院数学与计算机科学学院教师,理学硕士;陈 萍(1968-),女,河北衡水人,衡水学院数学与计算机科学学院教授.

(责任编校：李建明英文校对：李玉玲)