“几何画板”作分段函数图像
陈永胜,董 达
(吉林师范大学 数学学院,吉林 四平 136000)
“几何画板”作分段函数图像
陈永胜,董 达
(吉林师范大学 数学学院,吉林 四平 136000)
几何画板是一个优秀的专业学科平台软件,它以数学为根本,以“动态几何”为特色来动态表现设计者的思想,为探索几何奥秘提供一个新的工具.本文研究了使用“几何画板”画分段函数图像,给出详细的制作步骤.
几何画板;动态几何;分段函数
几何画板是一个适用于几何教学的软件平台,它以点、线、圆为基本元素,通过对这些元素的变换、构造、测算、计算、动画、跟踪轨迹等,能显示或构造出较为复杂的图形.它最大的特色是“动态性”,即:用鼠标拖动图形上的任一元素(点、线、圆),而事先给定的所有几何关系都保持不变,这样更有利于在图形的变化中把握不变,深入几何的精髓,突破了传统教学的难点[1].
分段函数是指自变量在不同的取值范围内,其对应法则也不同的函数.分段函数是一个函数,而不是几个函数;分段函数的定义域是各段定义域的并集,值域是各段值域的并集.以分段函数为载体的问题已成为高考中的热点问题.在绘制图像时,函数的定义域是不同的,我们首先采用分段法绘制复杂的函数的图像[2].
方法一:分区间作函数法
制作思路和步骤:将数轴x分成3个区间x1∈(− ∞,a),x2∈[a,b],x3∈(b,+ ∞),在每个区间上作线段或者射线,并分别取一个对象点A1,A2,A3度量它们横坐标x1,x2,x3.分别以x1,x2,x3为自变量,在相应的区间上构造计算公式f1(x1),f2(x2),f3(x3),分别选中点对(x1,f1(x1))、(x2,f2(x2))、(x3,f3(x3)),绘制点F1,F2,F3.再分别选中点A1和F1,A2和F2,A3和F3求作轨迹,绘出不同颜色的函数图像[3-4].
1) 打开一个新画板,选择<图表/定义坐标系>,建立直角坐标系.选择<图表/隐藏网格>,选择<编辑/参数选择>,打开“参数选择”对话框,将角度单位由“度”改为“弧度”.选择<图表/绘制点P(x,y)>,分别绘制出点A(−1,0)、B(4,0).用画点工具在点A的左侧x轴上,画一点C.先后选点A、C,选择<作图/射线>,画射线AC;先后选点A,B,选择<作图/线段>,画线段AB;用画点工具在点B的右侧x轴上,画一点D,先后选点B,D,选择<作图/射线>,画射线BD.分别在射线AC上取一个对象点1A,在线段AB上取一个对象点A2,在射线BD取一个对象点上取一个对象点A3,选中1A,A2,A3,选择<度量/横坐标>,度量它们的横坐标x1,x2,x3.
2) 选择<图表/新建函数>,新建以下几个函数f1(x) = cos(x),f2(x) = 2sin(x−1),f3(x) = sin(x) + cos(x).选择<度量/计算>打开计算器计算,分别以x1,x2,x3为自变量,计算3个函数值f1(x1),f2(x2),f3(x3).选点对(x1,f1(x1))、(x2,f2(x2))、(x3,f3(x3)),选择<图表/绘制点P(x,y)>,绘制点F1,F2,F3.再分别选点A1和F1,A2和F2,A3和F3,选择<作图/轨迹>,绘出不同颜色的分段函数图像(见图1).

图1 分区间作出的分段函数图像
首先将数轴x分成n个区间x1∈(− ∞,a1),x2∈ [a1,a2),…,xn∈ [an−1,+ ∞).在每个区间上作线段或者射线,分别取一个对象点A1,A2…,An,度量它们横坐标x1,x2,…,xn,分别以x1,x2,…,xn为自变量,在相应的区间上构造计算公式f1(x1),f2(x2),…,fn(xn),分别选中点对(x1,f1(x1)),(x2,f2(x2)),…,(xn,fn(xn)),绘出点F1,F2,…,Fn,分别选中点A1和F1,A2和F2,…,An和Fn求作轨迹,绘出不同颜色的函数图像.
方法二:构造符号函数法


在分段函数的定义域内,用画点工具在x轴上任取一点A,度量A的横坐标xA.计算F(xA) =s1(xA)∗f1(xA) +s2(xA)∗f2(xA) +s3(xA) ∗f3(xA)的值. 先后选中xA和F(xA)的值,作点B;同时选中A和B,求作轨迹即可.
1) 打开一个新画板,选择<定义/建立坐标系>,建立直角坐标系,选择<图表/隐藏网格>,选择<编辑/参数选择>,打开“参数选择”对话框,将角度单位改为“弧度”.选择<图表/新建函数>,依次新建以下几个函数s1(x) = (1− sgn(x+ 1))/2,s2(x) = (sgn(x+ 1)+ sgn(4 −x))/2,s3(x) = (1+ sgn(x− 4))/2,f1(x)= cos(x) ,f2(x) = 2sin(x− 1),f3(x) = sin(x) + cos(x).
2) 选中x轴,选择<作图/对象上的点>,在x轴上取任意点A,选中A,选择<度量/横坐标>,度量点A的横坐标xA. 打开计算器计算的值.将其名称改为yA,先后选中xA和yA的值,选择<图表/绘制点P(x,y)>,作点B;同时选中点A和点B,选择<作图/轨迹>即可(见图2).

图2 符号函数法作出的函数图像
般:首先依次新建以下n个函数

在x轴上取任意点A,度量A的横坐标xA,计算值.将名称改为yA,选中xA和yA的值,选择<图表/绘制点P(x,y)>,作点B;同时选中点A和点B,选择<作图/轨迹>即可.
如果所作分段函数的区间 (−∞,a1), [a1,a2),…,[an−1,+ ∞ )有些需要变化,也就是a1,a2,…,an的有些数值不固定,仍然可以作出它的图像.只需要利用<图表/新建参数>,分别建立参数a1,a2,…,an,并给出初值,当图像完成后,对于那些需要改变值的参数,可以选中参数后右单击,在快捷菜单中选择<属性/值>,改变参数的值,在快捷菜单中选择<属性/参数>,改变参数的变化方式(连续的或不连续的).
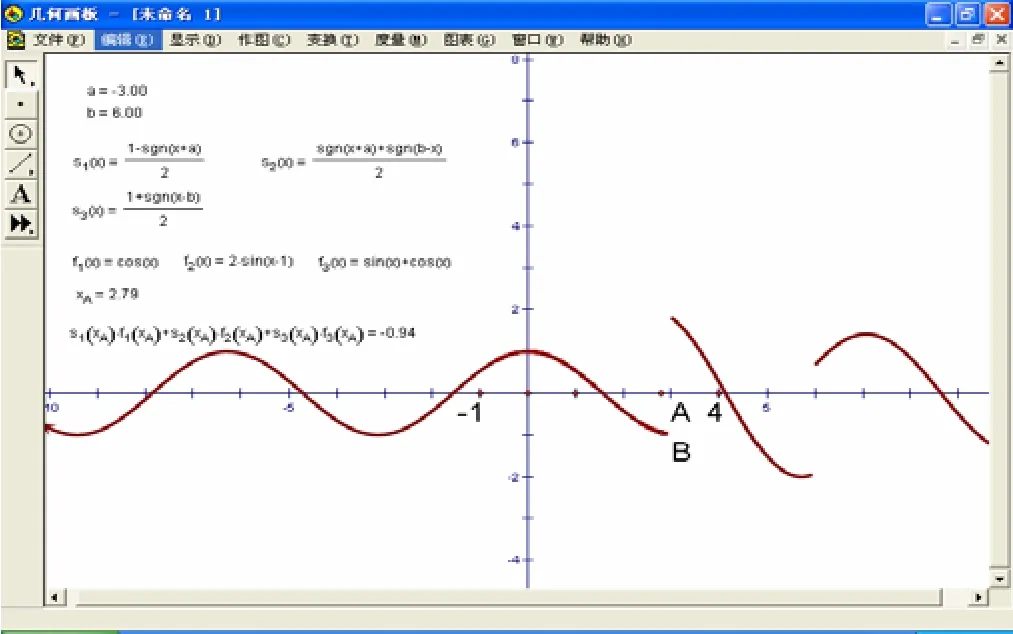
图3 符号函数法作出的任意区间的分段函数图像
[1] 刘胜利.几何画板与微型课件制作[M].北京:科学出版社,2004:130-132.
[2] 毛美生.如何在《几何画板》中绘制分段函数的图像[J].中学数学月刊,2002(3):24-25.
[3] 陶维林.几何画板与数学教学整合的实践与思考[J].中小学教材教学,2005(6):34-37.
[4] 廖学军.“几何画板”在数学教学中的应用[J].四川教育学院学报,2005(4):9-10.
Draw Graph of Partition Function with “The Geometer’s Sketchpad”
CHEN Yong-sheng,DONG Da
(College of Mathematics, Jilin Normal University, Siping, Jilin 136000, China)
The Geometer’s Sketchpad is outstanding specialized discipline platform software. It takes mathematics as the basis, "the dynamic geometry" as the characteristic to show dynamically the designer’s thoughts, and provides a new tool to explore the geometry mystery.This article discusses how to use " The Geometer’s Sketchpad " to draw partition function, and illustrates the steps in detail.
The Geometer’s Sketchpad;dynamic geometry;partition function
O17; G633.6
A
1673-2065(2011)04-0030-04
2011-02-19
吉林省高等教育教学研究重点课题(2010068); 吉林师范大学2009年校级教研立项重点课题(jsjy200921)
陈永胜(1973-),男,吉林长春人,吉林师范大学数学学院副教授,理学硕士;董 达(1989-),女,吉林白城人,吉林师范大学数学学院2008级学生.
(责任编校:李建明英文校对:李玉玲)

