一类可变量分离方程的解法探讨

汪 凯

（安徽财经大学 统计与应用数学学院, 安徽 蚌埠 233030）

一类可变量分离方程的解法探讨

汪 凯

（安徽财经大学 统计与应用数学学院, 安徽 蚌埠 233030）

研究了一类可变量分离方程的求解方法，并给出了在满足一定条件下求解这类方程更简单的方法.

常微分方程; 变量分离; 通解

0 引言

在王高雄等[1]、东北师范大学数学系方程教研室[2]以及丁同仁等[3]编写的常微分方程教程中均给出了一类可变量分离方程:

的一般求解方法, 该解法共分为3种情形:

1) 当a1/a2=b1/b2=c1/c2=k(常数)时, 方程(1)可化为dy=kdx, 其通解为y=kx+c, 其中c为任意常数. 2) 当a1/a2=b1/b2=k≠c1/c2时, 令u=a2x+b2y，方程(1)可转化为

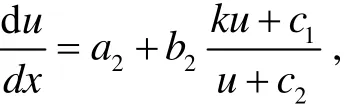
该方程为可变量分离的, 接下来根据变量分离方程的求解方法易求得其通解.

然后再根据齐次方程的求解方法求解. 具体求解过程如下:

先求解下列方程组

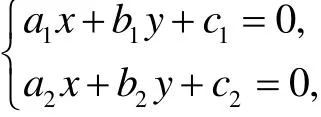
得其交点为(x,y) =(α,β), 再令

把(2)代入(1), 得

令u=Y/X, 则(3)化为如下变量分离的方程:

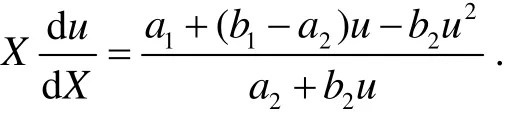
值得肯定的是该方法在求解这类方程时是很有效的, 但是对于后两种情形, 以上求解方法过于繁琐, 尤其是求解过程中涉及到多次的变量变换, 这给初学者的理解和掌握带来了一定的困难. 经过观察我们发现在方程(1)满足一定条件下还有更为简单的求解方法——凑微分法.

1 凑微分法

当方程(1)满足:

则有更简单的求解方法——凑微分法. 因为, 此时有

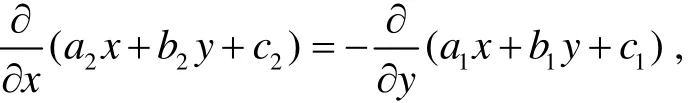
从而方程(1)可化为恰当方程, 即它是某个函数的全微分. 具体求解过程如下:

方程(1)可化为

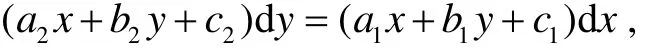
展开整理, 得

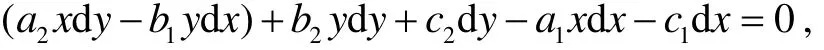
注意到条件(4), 从而

于是

这是一个全微分, 从而原方程的通解为 2a2xy+b2y2+ 2c2y−a1x2− 2c1x=c, 其中c为任意常数.

2 举例

下面通过例子加以比较说明我们所给出的凑微分解法更为简洁明了.

解法1该方程属于情形2). 令u=x−y, 则du/dx= 1− dy/dx, 于是原方程化为

解法2由于原方程右端函数满足条件(4), 从而由凑微分法有

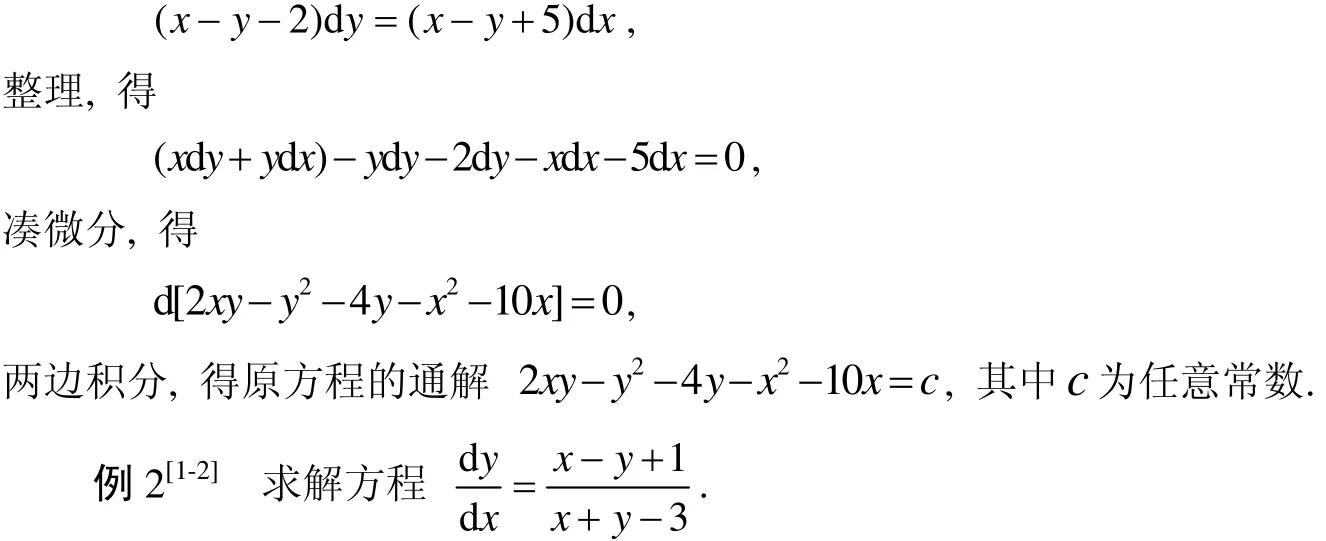
解法1显然该方程属于情形3). 首先解方程组

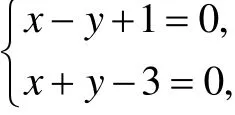
得x=1,y=2. 令x=X− 1,y=Y− 2,代入原方程得

再令u=Y/X, 即Y=uX, 则上式化为

两边积分, 得

因而

同时注意到22 1

u+u−=0也是原方程的解, 从而有

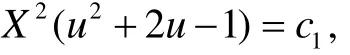
其中c1为任意常数. 带回变量u=Y/X, 得

再带回变量X=x− 1,Y=y− 2, 得

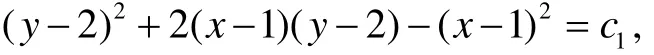
于是原方程的通解为y2+ 2xy− 6y− 2x−x2=c, 其中c=c1− 7为任意常数.

解法2因为方程右端函数的系数满足a2+b1= 0, 即条件(4)成立, 于是可用凑微分法来求解该方程.

由原方程得

展开整理, 得

凑微分, 得

两边积分, 得原方程的通解y2+ 2xy− 6y− 2x−x2=c, 其中c为任意常数.

3 结论

通过以上两个例子不难看出, 对于满足条件(4)的可变量分离方程(1), 我们所给出的凑微分求解方法要比文献[1-3]中所给出的解法简单很多. 特别是当方程(1)属于情形3)时, 此时若用我们所给的方法求解, 那么中间不涉及到任何变量变换, 因而求解过程非常简洁, 更有利于学生掌握和运用.

[1] 王高雄,周之铭,朱思铭,等.常微分方程[M].北京:高等教育出版社, 2006:36-39.

[2] 东北师范大学数学系方程教研室.常微分方程[M].北京:高等教育出版社,1982:23-26.

[3] 丁同仁,李承治.常微分方程教程[M].北京:高等教育出版社,2004:40-41.

Study on Solution for a Kind of Variables Separated First-order ODE

WANG Kai
(School of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu, Anhui 233030, China)

In this paper, the solution for a kind of variables separated first-order ODE is studied, and a simple method under some conditions is given.

ODE; variables separated; general solution

O175.6

A

1673-2065(2011)04-0013-03

2011-03-02

汪 凯(1977-),男,安徽泾县人,安徽财经大学统计与应用数学学院讲师,理学硕士.

(责任编校：李建明英文校对：李玉玲）