浅析幂指函数的极限问题
陈 茜 , 舒慧颖
(中南林业科技大学 a. 理学院;b. 商学院,湖南 长沙 410004)
浅析幂指函数的极限问题
陈 茜a, 舒慧颖b
(中南林业科技大学 a. 理学院;b. 商学院,湖南 长沙 410004)
对幂指函数求极限的问题,提出了几种方法,尤其讨论了等价无穷小替换在幂指函数求极限过程中的可行性.并且以实例演练了理论的应用性.
幂指函数;极限;洛必达法则;等价无穷小
幂指函数的一般形式为y=f(x)g(x)(f(x)>0),求幂指函数的极限是高等数学教学中的重点,也是难点.在考研数学以及期末统考中经常出现这样的题目.但是有些同学觉得无从下手?原因主要是对幂指函数的概念模糊,误认为幂指函数是幂函数或指数函数,其次在一般的教材中对幂指函数求极限的方法讲解的较少.在实际的教学中,针对这些问题,我们给出以下几例.
1 洛必达法则求极限[1]138.

2 等价无穷小求极限.
对于等价无穷小替换是否可以应用在幂指函数求极限的过程中,教材上一般没有涉及.为此,我们探讨了以下定理.
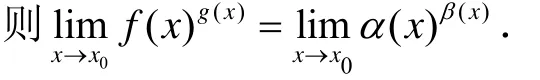

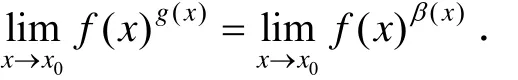

对于1∞型的幂指函数极限也可以用下面的定理解决.
定理2设f(x)与g(x)在x0的某一去心邻域内为连续函数,且当x→x0时,f(x) → 1,g(x)→∞,则

证明当x→x0时,f(x) →1,而 lnf(x) ~ [f(x)− 1],证明方法可仿照上例.


3 对于幂指函数极限其他类型的讨论.
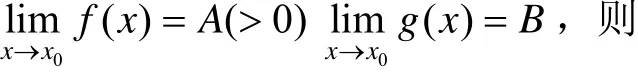
其证明可将幂指函数恒等变形后再利用连续函数的性质就可得到结论.
在上述的定理中若B=∞,那么通过讨论0<A<1和A>1可得到一些更详细的结论.同时,自变量x在其他的变化过程中,以上的结论仍是成立的.在这里,我们不再一一讨论.下面,就以下的例题来说明以上理论的应用.
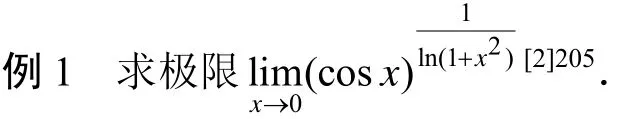



由上面的例题看来,将等价无穷小替换应用于幂指函数极限运算中,同时结合洛必达法则,无论是在解题过程还是计算上都要比传统的方法简捷.这就为学生们在学习及考试中提供了一条新的解题思路.
[1] 同济大学数学系.高等数学[M].北京:高等教育出版社, 2007.
[2] 黄先开,曹显兵,施明存,等.全国硕士研究生入学统一考试历届试题:理工数学一[M].北京:世界图书出版社,2004:25-223.
Analysis of Limit about Power-exponent Function
CHEN Qiana,SHU Hui-yingb
(Central South University of Forestry and Technology, a. School of Science; b. Business School, Changsha, Hunan 410004, China)
Several methods about limit of power-exponent function are provided. Especially, the application of equivalent infinitesimal replacement is proved. And the theory is described by some examples.
power-exponent function; limit; L’Hospital law; equivalent infinitesimal replacement
O172
A
1673-2065(2011)04-0008-03
2011-02-29
湖南省教育厅资助项目(09B113)
陈 茜(1977-),女,河北邢台人,中南林业科技大学理学院讲师,理学硕士;舒慧颖(1985-),女,苗族,湖南怀化人,中南林业科技大学商学院硕士研究生.
(责任编校:李建明英文校对:李玉玲)
———理学院

