C标尺洛氏硬度试验的不确定度评定

叶志飞,黄显芝,李 扬

广东省工业技术研究院(广州有色金属研究院),广东广州510650

C标尺洛氏硬度试验的不确定度评定

叶志飞,黄显芝,李 扬

广东省工业技术研究院(广州有色金属研究院),广东广州510650

根据C标尺洛氏硬度试验中标准硬度块、硬度计及试样等影响不确定度的因素,提出一种试验室洛氏硬度测量值不确定度的评定的方法,即通过对产生不确定度的若干分量的计算,最后计算出扩展不确定度.被测试样的扩展不确定度U=0.62HRC,硬度值的相对偏差小于1%,表明不确定度对试验的影响在可接受范围之内.

不确定度;洛氏硬度;C标尺

近年来,试验结果不确定度的评定越来越受到重视.一方面,一些企业、机构不但要求提供目前我国通用的检定证书,而且还要求提供校准报告,其中包括测量不确定度报告.另一方面,硬度计是测量洛氏硬度的手段,使用中必须进行周期检定,以确保硬度计的性能满足试验要求.而对硬度计期间检查的结果进行不确定度评定,能有效地评估硬度计的状况是否能满足工作所需.所以,硬度试验结果不确定度的评定,越发显示出其重要性.

本文中所使用的硬度计为经检定的 HR-150A洛氏硬度计,依照 GB/T 230.1-2009金属材料洛氏硬度试验方法,进行C标尺洛氏硬度试验.在计算不确定度时,主要考虑了与硬度计和试样相关的因素,而由于硬度计间接检定的原因,加入了标准硬度块(CRM)的影响.根据试验结果不确定度产生的来源,阐述了引入各分量的原因及数理依据,通过计算各分量的合成不确定度,最终求出扩展不确定度.

1 硬度值计算公式

洛氏硬度试验法采用顶角为120°的金刚石圆锥或直径为1.5875 mm或3.175 mm的硬质合金球作为压头,在初始试验力 F0和主试验力 F1共同作用下,将压头压入试样表面,保持规定的时间后卸除主试验力 F1,在保留初始试验力 F0的情况下测量残余压痕深度 h,洛氏硬度值计算公式如下:

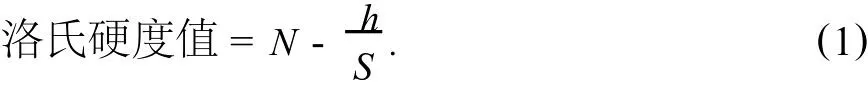
式(1)中 N和S为常数,因洛氏标尺不同而异.

对于C标尺洛氏硬度(HRC),规定N=100,即洛氏硬度值的最高值为100.当压痕深度残余增量为0.2 mm时,洛氏硬度值为零.将0.2 mm的压入深度划分为100等分,以等分0.002 mm定为1个洛氏硬度单位,即S=0.002.由此,C标尺的洛氏硬度值计算公式如下:

2 不确定度的分量计算

洛氏硬度试验不确定度的来源有很多,理论上环境温度、湿度及试验操作的稍许不同,都将对试验结果产生影响.如果把所有的因素均加以考虑,原则上不确定度的计算结果会更准确,但无疑会加大计算量,而且很多因素难以量化,势必削弱不确定度的评定结果的可比性.因此,在确保符合试验标准要求的前提下,忽略那些对不确定度影响甚微的因素,把焦点集中在硬度计与标准硬度块及试验过程上.

经分析,确定洛氏硬度测量值不确定度的来源主要包括标准硬度块的标准不确定度;用标准硬度块校验硬度计时的标准不确定度;测量试样硬度值的标准不确定度;压痕测量系统分辨力引入的标准不确定度;硬度计偏差引入的标准不确定度.

2.1 标准硬度块的标准不确定度 uCRM

为进行试验的不确定度评定,使用了经计量检定的洛氏标准硬度块,其硬度值 HCRM=62.4HRC,校准证书给出的扩展不确定度为0.3HRC,包含因子 k=2.因此,标准硬度块的标准不确定度计算如下:

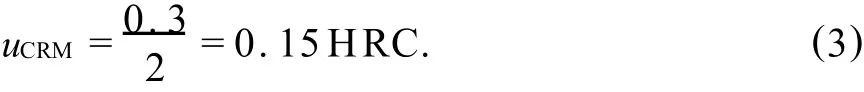
2.2 用标准硬度块校验硬度计的标准不确定度 uH—

硬度计示值的重复性是影响试验水平的重要因素.在日常使用中,实验室的硬度计是用标准硬度块来间接校验的,其示值受标准硬度块产生的不确定度影响.由于在不确定度的分量 uCRM中已考虑了标准硬度块的不确定度,为避免重复计算,因此在此分量中主要考虑硬度计示值重复性产生的不确定度.

为计算硬度计示值重复性产生的不确定度,先对 HCRM=62.4HRC的洛氏标准硬度块进行5个点的硬度测试,然后求硬度值的标准偏差,最后计算出硬度计的标准不确定度.5个压痕点的硬度测量值分别为62.4,62.5,62.5,62.1和62.3,平均硬度值H—=62.36.标准偏差sH的计算如下:

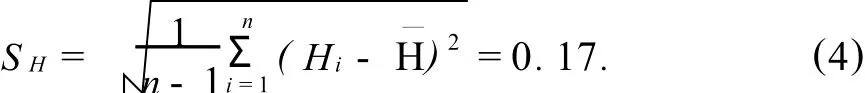
用标准硬度块校验硬度计的标准不确定度 uH—计算如下:

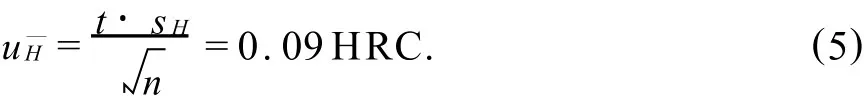
式(5)中,取 t=1.14,该值为 t分布在置信概率 p=68.27%,自由度 v=4时的值.

2.3 对试样进行洛氏硬度试验的标准不确定度 ux

该分量是硬度计示值重复性及试样材料均匀性复合产生的不确定度,基于避免重复计算,只考虑试样均匀性的因素.先对试样进行5个点的硬度值测量,然后求硬度值的标准偏差,最后计算洛氏硬度试验的标准不确定度.

试样5个压痕点的硬度值分别为66.4,66.1,66.4,66.2和66.3,平均硬度值 x-=66.28.5个测量值的标准偏差sx:

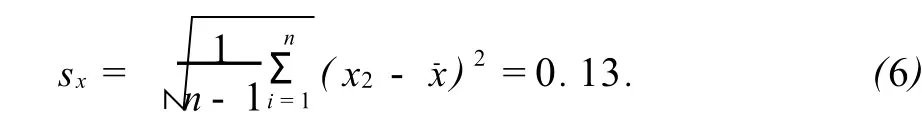
试样硬度值的标准不确定度ux计算如下:

式(7)中,取 t=1.14,该值为 t分布在置信概率 p=68.27%,自由度 v=4时的值.

2.4 压痕测量系统分辨力引入的标准不确定度ums

试验中使用的 HR-150A洛氏硬度计,测试分辨率δms=0.5HRC,按均匀分布考虑,压痕测量系统分辨力引入的标准不确定度 ums为:

2.5 硬度计偏差引入的标准不确定度 ub

硬度计在长期使用过程中,实验室环境及试验人员的操作等因素都会对硬度计的性能产生影响,从而使硬度计示值产生偏差.为监督硬度计的性能,可以用同一标准硬度块进行定期的日常检测,通过多组检测数据的标准偏差来计算不确定度.

在计算 uH—分量中,采用 HCRM=62.4HRC的洛氏标准硬度块.为了便于比较和计算,所测标准硬度块的不同时期的硬度值列于表1.

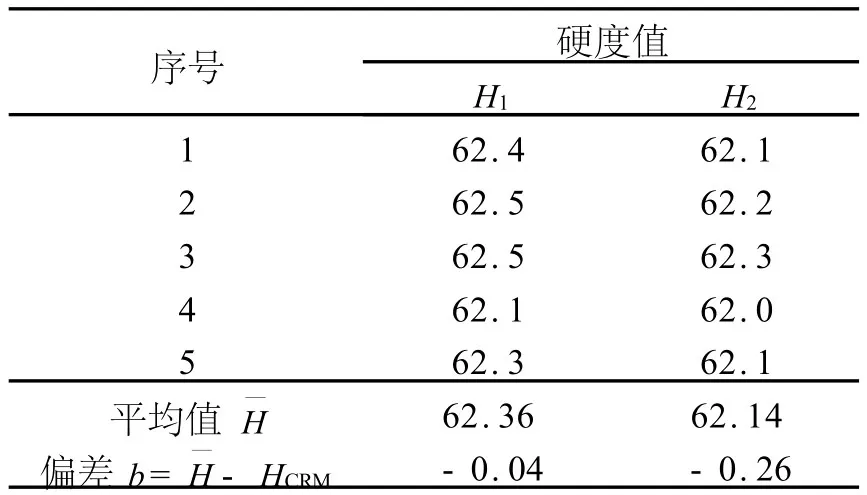
表1 HCRM=62.4HRC标准硬度块不同时期的硬度测量值Table 1 Periodicalmeasurement of hardness-reference block HCRM=62.4HRC

硬度计的偏差为测量的平均值与标准硬度块标定值之差,即 b=H—-HCRM.硬度计偏差的平均值b—及其标准偏差sb计算如下:

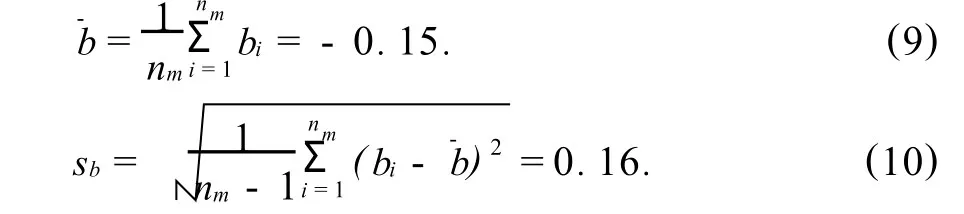
硬度计偏差引入的标准不确定度 ub计算如下:

式(11)中,取 t=1.84,该值为 t分布在置信概率

p=68.27%,自由度 v=1时的值.

3 扩展不确定度U

3.1 扩展不确定度 U的计算

对于试验室洛氏硬度测量值不确定度的评定,一般是通过计算出各分量不确定度,然后计算出合成标准不确定度 uc,最后由合成不确定度 uc和包含因子k得到扩展不确定度U.表2为不确定度各分量的评定结果.

表2 不确定度各分量的评定结果Table 2 Evaluation results of sources of uncertainty

合成标准不确定度uc计算如下:

扩展不确定度U是由合成不确定度uc乘以包含因子 k得到的.一般情况下,取置信度为95%,k=2.扩展不确定度U计算如下:

为考察扩展不确定度对试验的影响程度,试样硬度值的相对偏差为U值与试样的平均硬度值x-的百分比.本次试验的试样硬度的相对偏差=0.62/66.28=0.9%,表明不确定度对试验的影响在可接受范围之内.

3.2 测量结果的表示

在考虑硬度计偏差的情况下,洛氏硬度的测量结果按下式表示:

对于本次洛氏硬度试验的试样,X=(66.3±0.8),其中包含因子 k=2.

4 结 论

(1)在95%置信度下,本次C标尺洛氏硬度试验的扩展不确定度U=0.62HRC,被测试样硬度值的相对偏差小于1%.表明,不确定度对试验的影响在可接受范围之内.

(2)根据本次对不确定度各分量的评定可以看出,C标尺洛氏硬度试验的不确定度主要来自于硬度计和标准硬度块引入的不确定度分量,试验过程与人员引入的不确定度分量较小.因此,在日常检测工作中除严格按照标准进行试验外,还应重点关注硬度计和标准硬度块的工作状态,在定期检定与校准之外加强对硬度计和标准硬度块的期间核查.

[1]朱林茂,高怡斐,刘卫平,等.GB/T 230-2009金属材料洛氏硬度试验[S].北京:中国标准出版社,2009

[2]李慎安,施昌彦,刘风.JJF 1059-1999测量不确定度评定与表示[S].北京:中国计量出版社,1999.

[3]International O rganization fo r Standardization.ISO 6508-2005 metallic materials-rockwell hardness test[S].Sw itzerland:H IS,2005.

[4]温其诚,王京.JJG 2067-90金属洛氏硬度计量器具[S].北京:中国计量出版社,1990.

[5]李久林,肖红,国外标准中洛氏硬度值测量不确定度的评定方法对比与分析[J].物理测试,2006,24(1):49-54.

Uncertain ty evaluation of scale C rockwell hardness test

YE Zhifei,HUANG Xianzhi,L I Yang
Guangdong General Research Institute of Industrial Technology(Guangzhou Research Institute of Non-ferrous M eta ls,Guangdong Guangzhou 510650,China

This paper p roposes amethod on the evaluation of uncertainty of scale C Rockwell hardness test,in w hich those uncertainties associated w ith hardness-reference blocks,hardness tester,and specimen are taken into account.In other wo rds,the effect on the separated uncertainties is calculated to derive the expanded uncertainty.The expanded uncertainty of test piece U=0.62HRC,and the relevant deviation of hardness w ithin 1%show that the effect of uncertainties on the experiment is accep table.

uncertainty;rockwell hardness;scale C

TF123.121

A

1673-9981(2011)02-0164-03

2011-02-28

叶志飞(1973—),女,广东新会人,助理工程师.