一道德国奥数题的巧解和错解引发的探究

●

(南通高等师范学校 江苏南通 226100)

一道德国奥数题的巧解和错解引发的探究

●曹军

(南通高等师范学校 江苏南通 226100)

2008年德国数学奥林匹克有如下一道题目：

题目求最小的常数c，使得对所有的实数x，y，有

1+(x+y)2≤c(1+x2)(1+y2)．

《中等数学》2009年增刊第191页给出如下巧解：

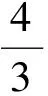
化简整理得

(2x-y)2+(x-y)2≥0,

解法21+(x+y)2≤c(1+x2)(1+y2)等价于

cx2y2+(c-1)(x2+y2)-2xy+c-1.

(1)

令x=y=0，得c≥1，于是

cx2y2+(c-1)(x2+y2)-2xy+c-1≥

cx2y2+2(c-1)xy-2xy+c-1=

cx2y2+2(c-2)xy+c-1.

(2)

令xy=t，则t∈R，设f(t)=ct2+2(c-2)t+c-1.若f(t)≥0恒成立，则

(2c-4)2-4c(c-1)≤0，

解得

解法1的确太神秘了，就像从魔术师的帽子里突然钻出兔子一样，让人匪夷所思.解法2虽比解法1自然，但遗憾的是解法有误，于是笔者作了一番探究，现将探究过程整理出来，和大家分享．

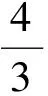
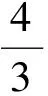
g(x,y)=cx2y2+(c-1)(x2+y2)-2xy+c-1，

f(xy)=cx2y2+2(c-2)xy+c-1.

解法3(解法2的修正)

(1)当c≥2时，满足题意.事实上,只需验证

1+(x+y)2≤2(1+x2)(1+y2)，

化简得

(x-y)2+2x2y2+1≥0，

这是显然成立的.而

2(1+x2)(1+y2)≤c(1+x2)(1+y2)，

因此

1+(x+y)2≤c(1+x2)(1+y2).

(2)当c<2时，在原不等式中令x=y=0，得c≥1，于是

1≤c<2.

从而1+(x+y)2≤c(1+x2)(1+y2)等价于

cx2y2+(c-1)(x2+y2)-2xy+c-1≥0.

(3)

令g(x,y)=cx2y2+(c-1)(x2+y2)-2xy+c-1，则不等式(3)恒成立的充要条件是g(x,y)min≥0.

下面求g(x,y)min：由基本不等式x2+y2≥2xy,得

g(x,y)≥cx2y2+2(c-2)xy+c-1,

(4)

当且仅当x=y时，等号成立.记f(xy)=cx2y2+2(c-2)xy+c-1,令xy=t，则

f(xy)=f(t)=ct2+2(c-2)t+c-1(t∈R)，

因此

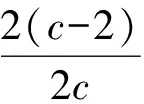
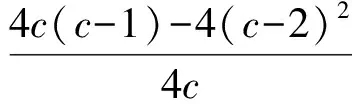
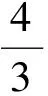
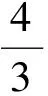
以上解法不但修正了解法2，而且揭开了解法1的神秘面纱，真可谓一举两得．其实，错误的解法都有某些合理的因素，充分挖掘并运用这些合理因素往往能修正错误的解法，甚至有时还能启迪新的解题思路．进一步反思解法2，它是利用基本不等式放缩，转化为一元二次不等式恒成立问题，利用判别式求解．然而已知的不等式本来既可以看作关于x的一元二次不等式，也可以看作关于y的一元二次不等式，因此利用基本不等式放缩显得多余，由此引发了下面的创新解法.

解法4不等式1+(x+y)2≤c(1+x2)(1+y2)可化为

令x=y=0，得c≥1．对任意x,y∈R，式(6)恒成立等价于

Δ=4y2-4(cy2+c-1)(c-1)(y2-1)≤0

对任意y∈R恒成立，整理得

c(c-1)y4+c(2c-3)y2+(c-1)2≥0.

令y2=t，则等价于

c(c-1)t2+c(2c-3)t+(c-1)2≥0

对任意t∈[0,+∞)恒成立．

当c=1时，显然不符合题意；

该赛题是一道含参数的恒成立问题，另一种常规思路是分离参数后转化为最值问题，如果先分离参数，会怎样呢？

解法5x,y∈R，1+(x+y)2≤c(1+x2)(1+y2)等价于对任意x，y∈R，有

(7)

即

(8)

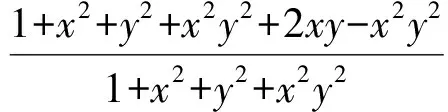
(9)

注意到式(9)的分子、分母中3处出现了xy，结合分母中的x2+y2，自然想到用基本不等式x2+y2≥2xy来放缩，但必须考虑2xy-x2y2的正负．由式(9)可知，M的最大值在2xy-x2y2>0时取得，于是不妨设2xy-x2y2>0(即0

当且仅当x=y时，等号成立.

即

(2)配方法

解法3至解法5的共同特征都是先求出c的取值范围，再确定c的最小值.解题过程比较繁琐，有没有简捷的解法呢?自然会联想到解法1.解法1虽神秘巧妙，令人匪夷所思，但它却凸现了一个很重要的解题思想方法——先求必要性再验证充分性，借鉴这种思想方法，将解法1稍作修改，可得解法6.

解法6由于式(7)对任意的实数x,y都成立，当然在特殊情形x=y下也成立，于是得到了式(7)的一个必要条件，即对任意x∈R，都有

即

接下来验证充分条件，同解法1．

这道竞赛题的探究历程至少给我们如下2点启示：第一，任何一种解法都有一定的价值，错解也不例外，其价值有时并不在于错误本身，而在于从中可以挖掘合理因素，修正错误解法，化失败为成功，甚至还能启迪创新思路，因此教学中要注重错误资源的有效利用;第二，问题的巧解不是凭空产生的，它往往依托于通性解法，因此教学中既要注重教通法，又要注重教反思，通过引导学生对通法进行反思，使学生在反思中看到转变思维的方向、方式、方法和策略，尽快获得成功.这不仅使学生感到巧妙思路的到来是顺其自然的，而且在发展学生思维、培养创新能力上无疑是一种很好的体验和进步．

[1] 高孝君．一道德国数学奥林匹克试题的解答[J]．数学通讯(上半月)，2010(11-12)：117．