圆锥曲线与焦点弦的中点及准点有关的一个性质

●

(常德市第六中学 湖南常德 415003)

圆锥曲线与焦点弦的中点及准点有关的一个性质

●彭世金

(常德市第六中学 湖南常德 415003)

笔者通过对圆锥曲线的探究,得到圆锥曲线与焦点弦的中点及准点(准线与对称轴的交点)有关的一个性质,现介绍如下.

图1

消去x,化简整理得

(a2+b2m2)y2+2b2cmy-b4=0.

设A(x1,y1),B(x2,y2),则

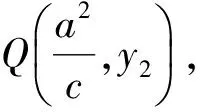
于是

从而直线AE的斜率为

直线PQ的斜率为

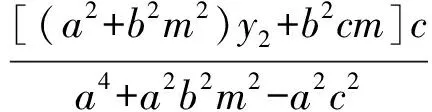
因为

kAE-kPQ=

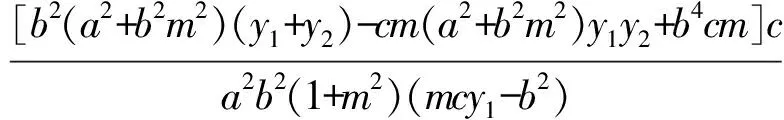
所以

kAE=kPQ,

即

AE∥PQ.

图2

图3

性质3如图3,已知抛物线y2=2px(p>0),AB是抛物线过焦点F的弦,抛物线的准线l与对称轴的交点为E,点B在准线l上的射影为Q,点P是弦AB的中点,则AE∥PQ.

性质2、性质3类似于性质1可证,此处从略.