七巧板能拼出多少种凸多边形

●

(大堰初中 浙江奉化 315509)

七巧板能拼出多少种凸多边形

●董孟雄

(大堰初中 浙江奉化 315509)

1 问题的提出

问题对正方形ABCD按如图1所示划分,其中E,F分别是BC,AB的中点,M,N,G分别是OA,OC,EF的中点,沿分划线可以剪出一副由七块部件组成的“七巧板”.设正方形OGFM的边长为1.请用这幅七巧板既不留下一丝空隙,又不相互重叠,各拼出1种周长最大与最小的凸多边形,画在图2中,并计算最大周长与最小周长各是多少？

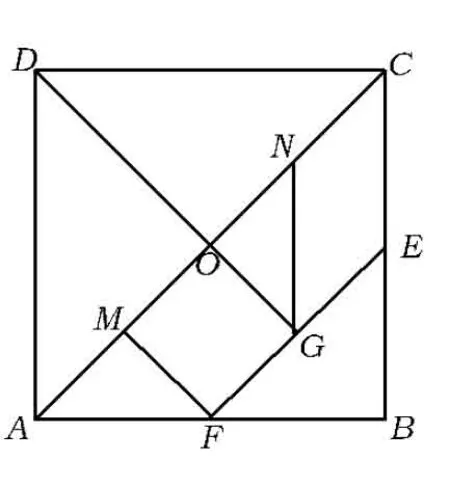
图1

图2

图3

图4

图3中的多边形周长为什么是最大的？图4中的多边形周长为什么又是最小的？笔者亦是百思不得其解,只能换个角度思考：七巧板到底能拼出多少种凸多边形？

2 问题的分析

图5

(2)7块部件的内角总和1 620°,其中有9个直角、12个45°角、2个135°角.

(3)不论拼成哪种多边形,其面积为常量8.

(4)可以从凸多边形的边数分类讨论.

3 问题的解决

3.1 拼成三角形

三角形的内角和等于180°,由七巧板角的特征,知只有180°=90°+45°+45°,因此拼成的三角形必为等腰直角三角形(唯一).因为面积为8,所以直角三角形的直角边长为4,如图6所示.

图6

图7

3.2 拼成四边形

四边形的内角和等于360°,由七巧板角的特征,知

360°=90°×4=90°×2+45°×1+135°×1=

135°×2+45°×2.

3.2.1 360°=90°×4

拼成的四边形为正方形或长方形.

若为正方形,则图形唯一确定,如图7所示;

长、宽分别为4,2的矩形如图8所示.

图8

图9

3.2.2 360°=90°×2+45°×1+135°×1

若2个直角相邻,则拼成的四边形为直角梯形.

若梯形的高为2,则上、下底之和为8,如图10所示.

图10

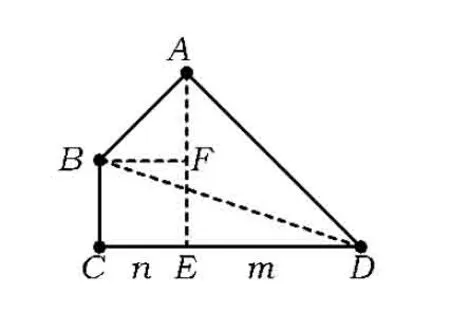
若2个直角不相邻,则所得四边形如图11所示.过点A作AE⊥CD于点E,过点B作BF⊥AE于点F,连结BD,如图12.设CE=n,ED=m,则

因为四边形的面积为8,所以

即

m2-n2+2mn=16.

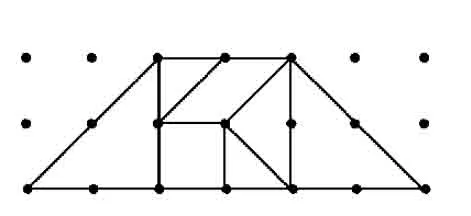
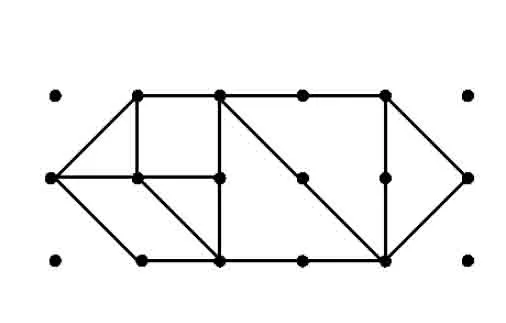
又由n

16=m2-n2+2mn>m2-n2+2n2>2n2，

即

n2<8,

解得

n=2或n=1.

当n=2或n=1时,m都不是整数.因此拼不出如图11所示的四边形.

图11

图12

3.2.3 360°=135°×2+45°×2

若2个135°角相邻,则拼成的四边形是等腰梯形,如图13所示.

若2个135°角相对,则拼成的四边形是平行四边形,如图14所示.

图13

图14

3.3 拼成五边形

五边形的内角和等于540°,由七巧板角的特征,知

540°=135°×3+90°×1+45°×1=

135°×2+90°×3.

3.3.1 540°=135°×3+90°×1+45°×1

若3个135°角相邻,则能构成这类五边形的最小面积为6.5,如图15.比它略大的五边形面积必超过8,所以这类五边形也不能拼成.

图15

图16

若3个135°角中的一个与其余2个不相邻,则拼成的五边形如图16所示.

3.3.2 540°=135°×2+90°×3

得x<4.因为x是偶数,所以

x=2.

当x=2时,mn=10,不存在大于2的整数解.

图17

图18

8=2ab-t2>t2,

得

t=2.

当t=2时,ab=6,不存在大于2的整数解.所以不存在这样的五边形.

若3个90°角中的一个与其余2个不相邻,则拼成的五边形如图18所示.

3.4 拼成六边形

六边形的内角和等于720°,由七巧板角的特征,知

720°=135°×5+45°×1=135°×4+45°×2.

4.4.1 720°=135°×5+90°×1

拼出的四边形面积至少为9.5,如图19,因此这类六边形不能拼成.

图19

图20

4.4.2 720°=135°×4+90°×2

若2个直角相邻,则拼成的六边形如图20所示;若2个直角不相邻,则拼成的六边形如图21,22,23所示.

图21

图22

图23

4.5 不能拼成七边形或八边形

七边形的内角和等于900°,由七巧板角的特征,知

900°=135°×6+90°×1,

这样的七边形最小面积为7.5,稍大些则必超过8,因此不能拼成七边形.

同理可得,也不能拼成八边形.

4.6 不能拼成边数大于8的多边形

因为七巧板能提供的最大内角为135°.对于n边形,有135n≥180(n-2),解得n≤8,所以不能拼成边数大于8的多边形.

至此,七巧板能拼出13种不同形状的凸多边形.

4 问题的反思

(1)本题周长的最大值或最小值很难(几乎不可能)从理论上证明,图形存在多样性,探讨情况也很复杂,因此这样的问题是否适宜当作笔试的题目？笔者认为这个问题更适宜当作一个课题,在课堂活动中探究.

(2)上述问题的解答过程或许有些环节不甚严密,请大家不吝指正.