圆锥曲线中一类过定点问题的统一性质

●

(启东中学 江苏启东 226200)

圆锥曲线中一类过定点问题的统一性质

●金山

(启东中学 江苏启东 226200)

笔者通过一个椭圆定点问题的探究,层层深入,最终将问题推广到圆锥曲线的一般情形.现将探究过程简述如下，与大家分享.

在此题中,直线AM和AN的斜率乘积为-1,直线MN经过一定点.当过顶点的这2条弦斜率乘积为任一定值时,直线MN还经过一定点吗?经过探究得到以下性质.

证明设M(x1,y1),N(x2,y2).不妨取顶点A(a,0)(其余情形证明类似),则

于是

(1)

(1)若直线MN斜率存在，设其方程为y=kx+m(k≠0).直线MN的方程与椭圆方程联立,消去y得

b2x2+a2(kx+m)2-a2b2=0.

因为x1,x2是它的2个根,所以

b2x2+a2(kx+m)2-a2b2=

(b2+a2k2)(x-x1)(x-x2).

记f(x)=(x-x1)(x-x2),则

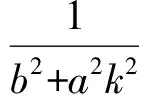
于是

y1y2=(kx1+m)(kx2+m)=

(2)

(3)

式(2)，式(3)代入式(1)得

解得

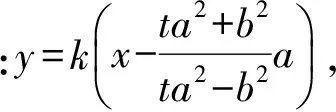
(2)若直线MN的斜率不存在，设其方程为x=m,则

代入式(1)得

解得

因此

即

设直线MN的方程为x=ky+m,代入抛物线方程消去x得

y2-2pky-2pm=0.

由韦达定理得

y1y2=-2pm,

因此

即

以上探讨了过圆锥曲线一条弦的2个端点与顶点连线斜率乘积为定值时,该弦过对称轴上的一定点.反之,经过对称轴上的一定点的弦的2个端点与顶点连线斜率是否为定值呢?经过进一步探究,得到以下结论.

证明(1)设M(x1,y1),N(x2,y2),不妨取右顶点为A(a,0).设直线MN的方程为x=ky+t,代入椭圆方程消去x得

b2(ky+t)2+a2y2-a2b2=0.

因为y1,y2是它的2个根,所以

b2(ky+t)2+a2y2-a2b2=

(b2k2+a2)(y-y1)(y-y2).

令f(y)=(y-y1)(y-y2),则

因此 (x1-a)(x2-a)=

(ky1+t-a)(ky2+t-a)=

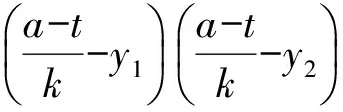
(2)略.