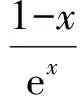貌似神离的两类恒成立
●
(苏苑中学 江苏苏州 215128)
貌似神离的两类恒成立
●杨品方
(苏苑中学 江苏苏州 215128)
1 提出问题
观察下面2个问题:
问题1已知f(x)=8x2+16x-a,g(x)=2x3+5x2+4x(a为实数),若对任意的x∈[-3,3]都有f(x)≤g(x)恒成立,求实数a的取值范围.
问题2已知f(x)=8x2+16x-a,g(x)=2x3+5x2+4x(a为实数),若对任意的x1,x2∈[-3,3]都有f(x1)≤g(x2)恒成立,求实数a的取值范围.
笔者发现,学生对这2个问题的求解很多是靠运气的,这次练习中做对了,下次测试中也许又做错了.究其原因,这2个问题虽然“貌似”但又“神离”,下面让我们来好好辨别.
2 观察问题
问题1中的“f(x)≤g(x)恒成立”,左、右两边所取“自变量”是同一个,譬如f(1)≤g(1),f(-2)≤g(-2),但又不包括如f(1)≤g(-2)等.事实上,f(1)与g(-2)是不能比较大小的,也没有必要去比较大小,如图1所示.
问题2中的“f(x1)≤g(x2)恒成立”,左、右两边所取“自变量”可以相同,还可以不相同,譬如f(1)≤g(1),f(1)≤g(-2)等.事实上,只要是f(x1),总有小于等于g(x2)的部分,如图2所示(图中水平虚线仅作分界,不是图像).

图1
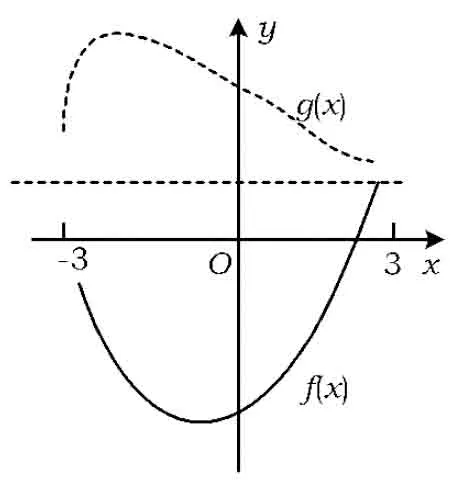
图2
问题2的条件比问题1的条件要“严格”,问题2中a的取值集合是问题1中a的取值集合的子集.
3 解答措施
问题1的解答通常是:记函数h(x)=f(x)-g(x),求出[-3,3]上h(x)的最大值h(x)max,解不等式h(x)max≤0,从而得到实数a的取值范围.此处
h(x)max=45-a≤0,
故a≥45.
问题2的解答通常是:分别求出[-3,3]上f(x)的最大值f(x)max,g(x)的最小值g(x)min,解不等式f(x)max≤g(x)min,从而得到实数a的取值范围.此处
f(x)max=120-a,g(x)min=-21,
从而
120-a≤-21,
故
a≥141.
4 应用举例
例1已知函数f(x)=lnx-ax2+(2-a)x.
(1)讨论f(x)的单调性;


(3)若函数y=f(x)的图像与x轴交于点A,B,线段AB中点的横坐标为x0,证明:f′(x0)<0.
(2011年辽宁省数学高考理科试题)
分析(1)略;
(3)略.
解(1)略;
g(x)=ln(1+ax)-ln(1-ax)-2ax,
求导得

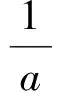

故
(3)略.

(1)用a表示出b,c;
(2)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围.
(2010年湖北省数学高考理科试题)
分析(1)略;
(2)不等式f(x)≥lnx的左、右两边是同一个变量x,应归属于“问题1”类型.
解(1)由题意可得

(2)由第(1)小题知


其中x∈[1,+∞),易得g(1)=0.为研究g(x),求导得




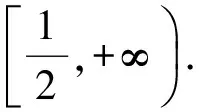

(2011年陕西省数学高考理科试题改编)
分析要证不等式的左、右两边是同一个变量x,应该归属于“问题1”类型.
解由题意可知

因此



当x>1时,h′(x)<0,h(x)在(1,+∞)内单调递减,因此
h(x) 从而 (1)当a=1时,求函数f(x)的最小值; 分析(1)略; 简解(1)f(x)的最小值为1(过程略). 例5已知函数f(x)=xlnx,g(x)=-x2+2ax-3. (1)求f(x)在区间[1,3]上的最小值; (2)若f(x),g(x)在区间[1,3]上单调性相同,求实数a的取值范围; (3)求证:对任意的x∈(0,+∞),都有 分析(1),(2)略; 于是 图3 貌似神离、似是而非的2个恒成立问题,因为左、右两边变量的不同,而导致答案数据相差甚远.通过上述实例的分析可以发现,解决这类问题之前要先判断问题属于哪一类.对于问题1类型的,需考虑差函数,研究该差函数的最大或最小值;对于问题2类型的,先分别求出2边的最大或最小值.尤其要注意的,也是最难的当属例5类型的,表面上是问题1类型(因为左右的变量相同),实际上是问题2类型(因为一边的最小与另一边的最大作比较),这也需要我们在解题受阻(像例5的分析)时能及时、有效地调整思路.