巧用“层次对称”求一类分式的最大值

●

(阳新县高级中学 湖北阳新 435200)

巧用“层次对称”求一类分式的最大值

●邹生书

(阳新县高级中学 湖北阳新 435200)

笔者在研读文献[1]时发现，该文中的几个不等式可通过另一种巧设参数妙拆分的构造法求得.若能充分挖掘和利用所含字母不同层次间的微妙的对称关系，则可少设参数甚至不设参数达到减少运算量之功效，从而体现多思少算的解题原则.现将其整理成文与读者分享.

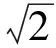
得

分析尝试从分母入手将平方和转化为积和，从而求出最大值.注意到所求式子4个字母a,b,c,d的微妙关系,可分为如下2个层次：其中a,d为第1层次，b,c为第2层次，各层次的字母地位相对平等对称，并且a与b之间的关系等同于d与c间的关系.根据以上分析，在应用重要不等式时，应将分母中的b2,c2分别等权地分给a2,d2搭配成对，这样才能体现这种既有等级层次又相对平等的微妙关系，因此有如下解法：

解a2+b2+c2+d2=

(a2+λb2)+(1-λ)(b2+c2)+λc2+d2≥

即

λ2-3λ+1=0.

因为0<λ<1，所以

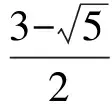
将其代入上述不等式得

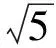
即

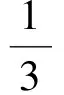
所以

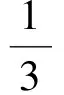
下面我们再用此法解一道含有参数的有关分式的最大值问题.

分析由题设知y,z对于x而言,地位相对平等对称，于是有如下解法：

解引入参数λ∈(0,1).由均值不等式得

x2+y2+z2=

即

所以

综上可知，求这类分式最值的方法是：根据分子中字母的“层次对称”这一结构特点，恰当地尽可能少地引入参数，将分母的平方和巧妙拆分合理搭配，然后用重要不等式“凑出分子”的积和式，再利用对应项系数成比例确定参数的值继而求出最大值.纵观本文数例不难发现：当所求式子取得最大值时，同一层次中的字母取值相同，不同层次的字母取值不同，即不同层次字母的取值成比例，这是一个非常有趣的现象.此结果表明字母在条件中具有层次性、平等性和对称性，在结果仍具有这三性，这一结果简直太美妙了，这使我们再次领略到数学的对称美、奇异美与和谐美.

[1] 张俊.一个平凡不等式引发的探究[J].数学教学，2010(12)：12-14.

[2] 邹生书.巧“设”妙“分”求最值[J].数学通讯(下半月)，2011(3)：31.

[3] 邹生书.运用对称探求最值[J].河北理科教学研究，2010(6)：3-5.