基于一种新的信息熵的区间直觉模糊集多属性决策分析

毛军军， 贾静丽， 张纪强， 孙 丽

（1．安徽大学 数学科学学院，安徽 合肥 230039；2．安徽大学 计算智能与信号处理教育部重点实验室，安徽 合肥 230039）

基于一种新的信息熵的区间直觉模糊集多属性决策分析

毛军军1，2， 贾静丽1， 张纪强1， 孙 丽1

（1．安徽大学 数学科学学院，安徽 合肥 230039；2．安徽大学 计算智能与信号处理教育部重点实验室，安徽 合肥 230039）

本文对权重未知的区间直觉模糊集进行了探讨。给出了基于犹豫度基础上区间直觉模糊集的得分函数，并提出新的信息熵及基于信息熵的权重表达式，最后给出基于此方法的区间直觉模糊集多属性决策分析方法，并用实例加以验证该方法是切实有效的。

区间直觉模糊集；得分函数；信息熵；权重；决策

1 引 言

自从Zadeh于1965年提出模糊集理论以来，该理论在现代社会的各个领域得到了广泛的应用。模糊集的隶属函数值仅是一个单一的值，保加利亚学者Atanassov对Zadeh的模糊集进行了拓展，把仅考虑隶属度的传统模糊集推广到同时考虑隶属度，非隶属度和犹豫度这三方面信息的直觉模糊集，并将其推广至区间的形式，定义了区间直觉模糊集的一些运算法则。文献［1］定义了区间模糊数的概念并给出了区间模糊数的基本运算法则，提出了区间直觉模糊集的加权平均算子和加权几何算子，在得分函数与精确函数的基础上给出了区间直觉模糊数的一种排序方法。文献［2］提出了直觉模糊集的得分函数法，文献［3］提出了区间直觉模糊集的得分函数法，本文对此方法做了改进。在权重未知的情况下，文献［4］中定义了基于信息熵的多属性决策方法，但是此方法受到一定程度的限制。基于此，在权重未知的情况下本文给出了一种新的信息熵及其权重的表达式。

2 区间直觉模糊集的基本理论

由于客观事物的不确定性与复杂性，直觉模糊集中的真隶属度与假隶属度很难用确定实数来表达，而比较适合用区间的形式来表示。为此，Atanassov和Gargov给出了区间直觉模糊集的概念：

3 一种改进的熵

熵是系统无序的度量，信息是系统有序程度的度量，两者绝对值相等，序号相反。某项指标的指标值离散程度越大，则信息熵越小，该指标提供的信息量越大，其权重也越大；反之指标的指标值离散程度越小，信息熵就越大，该指标提供的信息量就越小，权重也相应的越小。这时我们可以建立适当的指标体系，根据各项指标值的离散程度，利用信息熵确定指标的权重，可以对研究对象的定量评价提供科学依据。

该方法计算出的熵为Shannon熵，其取值范围为［0，＋∞），显然并不符合权值的要求。权值的取值范围为［0，1］，为此本文提出一种改进的熵的定义：

定义3．2 考虑一个具有n个结果的概率试验，并设这些结果各自具有离散概率pi，i＝1，…，n，则熵为

4 基于改进熵的权值的定义方法

定义4．1［5］设有n个方案，m 个评价指标（属性），则原始数据矩阵R＝（Xij）m×n对于第j个指标，有信息熵为Ej，熵Ej表示第j个指标的不稳定性，Ej越小，其提供的信息量越小，在综合评价中所起的作用越小，其权重也应越小。因此，第j个指标的的熵权（客观权重）

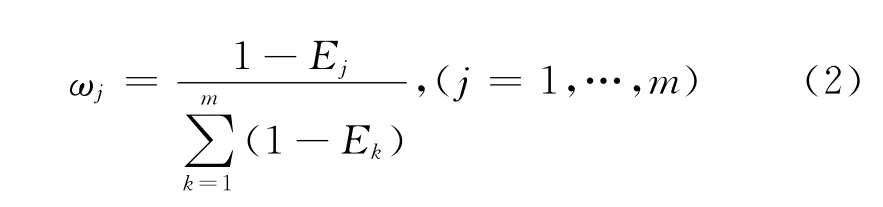
但是周惠成等在文献［7］中指出，此熵权公式存在以下问题：当各指标熵值Ej→1时，熵值间的微小变化可能引起不同指标熵权的成倍数的变化。如当指标熵值向量为（0．9，0．8，0．7）和（0．9999，0．9998，0．9997），熵值间的差值虽然不同，但由于1－Ej比例相同，熵权向量均为（0．1667，0．3333，0．5000），第二组指标向量的差值已经很小，但所得权向量却成倍数关系，熵值的微小扰动造成权值的过于敏感的变化，公式（2）夸大了噪声数据的影响，这显然与熵所表达的意义是不一致的，有必要对权值公式更新。为此本文给出了改进的熵权公式。

定义4．2 设有n个方案，m个评价指标（属性），则原始数据矩阵R＝（Xij）m×n对于第j个指标，有信息熵为Ej，第j个指标的权重为：

即证明了熵值的极小变化没有引起权值的成倍数的变化。

5 熵权法确定指标权重的步骤：

步骤7：利用zi（ω）（i∈N）对方案进行排序与择优，zi（ω）越大则方案越优。

6 实例分析

某单位在对干部进行考核选拔时，首先制定了六项考核指标（属性）：思想品德（G1），工作态度（G2），工作作风（G3），文化水平和知识结构（G4），领导能力（G5），开拓能力（G6），指标的权重向量未知。现假设有五位候选人Yi（i＝1，2，…，5）．且每位候选人在各指标下的评估信息经过统计处理后，可表示为区间直觉模糊数，如表1［1］所示。其中zi（ω）为候选人Yi的综合得分。

表1 区间直觉模糊决策矩阵~D

下面用本节中的方法确定各属性的客观权重，从而确定最佳候选人：

由矩阵~D利用公式（2．5．1）得分函数公式计算得分矩阵s＝（sij）n×m；再用坐标平移之后

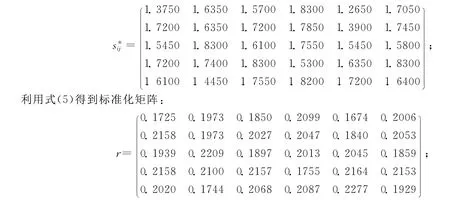
然后由（1）得 E1＝0．9193；E2＝0．9198；E3＝0．9528；

E4＝0．9238；E5＝0．8971；E6＝0．9558

进而由熵权公式 （3）得 ω1＝0．1728；ω2＝0．1725；ω3＝0．1494；ω4＝0．1697；ω5＝0．1883；ω6＝0．1473。

每个候选人的综合得分为，z1（ω）＝0．1882；z2（ω）＝0．2012；z3（ω）＝0．2000；z4（ω）＝0．2080；z5（ω）＝0．2026；

显然z4≻z5≻z2≻z3≻z1，即本文得出的排序中Y4为最佳候选人。

7 结束语

在对权重未知的区间直觉模糊集进行多属性决策时，本文提出了一种计算基于犹豫度的区间直觉模糊集的得分函数的方法，并提出了一种改进熵值及熵权的表达式，更符合熵值及熵权的意义。然后给出了计算权重未知的区间直觉模糊集多属性决策问题的方法步骤，最后结合实例验证本文中的方法切实可行。本文的研究结果具有客观性，排除人为因素的影响，可以直接应用到综合评价问题中。

［1］ 徐泽水．直觉模糊信息集成理论与应用［M］．北京：科学出版社，2008．

［2］ 万树平．基于Vague集的多属性群决策专家权重的确定［J］．应用数学与计算数学学报，2010，24（1）：45-52．

［3］ V．Lakshmana Gomathi Nayagam，S．Muralikrishnan，Geetha Sivaraman．Multi－criteria decision－making method based on interval－valued intuitionistic fuzzy sets［J］．Expert Systerms with Applications，2010，38（2011）：1464-1467．

［4］ 卫贵武．权重信息不完全的区间直觉模糊多属性决策方法［J］．管理学报，2008，5（4）：208-211，217．

［5］ 徐泽水．不确定多属性决策方法及应用［M］．北京：清华大学出版社，2004．

［6］ 陈红，毛虹保．一种新的基于粗糙集的案例特征权值确定方法［J］．西安工业大学学报，2010，30（4）：402-405．

［7］ 周惠成，张改红，王国利．基于熵权的水库防洪调度多目标决策方法及应用［J］．水利学报，2007，38（1）：100-136．

Multi-attribute decision-making analysis for interval-valued intuitionistic fuzzy based on a new entropy

MAO Jun-jun1，2， JIA Jing-li 1， ZHANG Ji-qiang1， SUN Li 1（1．School of Mathematical Sciences，Anhui University，Hefei，230039，China；2．Key Laboratory of Intelligent Computing ＆ Signal Processing of Ministry of Education，Institute of Artificial Intelligence Anhui University，Hefei 230039，China）

Interval-valued intuitionistic fuzzy set of unknown weight are investigated in this paper．A score function for interval-valued intuitionistic fuzzy set has been constructed based on hesitancy degree．An expression of a new entropy has also been proposed．Finally，decision-making approach for interval-valued intuitionistic fuzzy information has been developed，and a practical example is given to verify this approach is effective．

interval-valued intuitionistic fuzzy set；score function；entropy；weight；decision-making

TP18

A

1674-2273（2011）06-0001-05

2011－06－09

国家自然科学基金（61073117），安徽大学学术创新团队资助（KJTD001B）安徽高等学校青年基金项目（2011SQRL186），安徽大学人才队伍建设经费

毛军军（1973－），女，博士，副教授，主要研究方向是智能计算及其应用；贾静丽（1986－），女，硕士研究生，河北邯郸人，主要研究方向是统计与运筹决策。