综合素质评价的神经网络模型及Simulink实现
王 宁, 孙晓玲, 梁 艳
(合肥师范学院 数学系,安徽 合肥 230601)
综合素质评价的神经网络模型及Simulink实现
王 宁, 孙晓玲, 梁 艳
(合肥师范学院 数学系,安徽 合肥 230601)
针对大学生综合素质评价过程中存在诸多非定量因素及非线性特征,建立综合素质测评的BP神经网络模型。利用BP神经网络实现对量化评价函数的逼近。所给出的神经网络模型较已有的评价体系具有更高的执行效率,而且还能生成模块化的程序进行推广。利用Matlab软件的Simulink平台对BP神经网络进行仿真计算,该方法可操作性强,不需要进行模糊评测方法过程中的复杂运算,具有较广泛的实用性。
BP神经网络;模糊综合评判;综合素质测评
1 引言
影响大学生综合素质评价的因素很多,各因素的影响程度也不尽相同,因此,评价结果很难用一个数学解析式来表示。它是属于非线性的分类问题,这就给综合评价带来了较大的困难。传统的评价方法多是采用直接建立评价系统的数学模型,如层次分析法、聚类分析、灰色系统、模糊综合评判法等,但这些方法在评估过程中难以排除各种随机性和主观性,易造成评价结果失真和偏差。通过寻找合适的评价体系中的输入和输出的数学关系,建立一个合理的、科学的数学模型,将对大学生综合素质测评工作有着重要的意义。
神经网络是由大量处理单元组成的非线性自适应动态系统,它具有学习能力,记忆能力,计算能力以及智能处理功能,在不同程度层次上模仿大脑的信息处理机理。它可用于预测、分类、模式识别和过程控制等各种数据处理场合。相对于传统的数据处理方法,它更适合处理模糊的、非线性的和模式特征不明确的问题[1]。
本文把人工神经网络理论应用于大学生综合素质评价,给出了一种基于三层神经元的量化评价方法,通过对已知样本的学习,获得评价专家的经验、知识、主观判断,以及对目标重要性的权重协调能力,网络便可以再现评价专家的经验,知识和直觉思维,从而降低评价过程中人为因素的影响,从根本上克服大学生综合素质评价过程中建模与求解的困难,具有时间短、速度快、精度高的优点,较好的保证评价结果的客观性,对综合测评工作提供有意义的参考[2-4]。
2 大学生综合素质评价的指标体系及模糊评判规则
要建立大学生综合素质评价模型,首先要建立综合素质评价体系。根据高等学校大学生自身的特点,需要按照层次化的方法建立评测指标体系并确定各指标的权值,在不断的反馈和修改中得到比较满意的结果。
2.1 确定参评指标及权重向量
以某师范大学为例,根据师范大学学生的特点,现按照层次化的方法为待测对象建立评测指标体系,首先将顶级指标定义为总体,然后将总体细分为德,智,体,能四个一级指标。再将一级指标分为多个二级指标。还可以按照实际要求继续细分。这样所有的参评项目就构成了一个具有层次结构的指标树[5-7]。
2.2 模糊变换处理
在前面建立的指标体系中,假设评价指标集合为X={x1,x2,…,xn},其中xi(i=1,2,…,n)是评价因素。n是同一层次上单个因素的个数。假设评价结果的集合为V={v1,v2,…,vm}。其中vj(j=1,2,…,m)是评价结果,m是集合V中的元素个数,即等级数或评语档次数。评价结果集合规定了某一评价因素的评价结果的选择范围,结果集合中的元素既可以是定性的,也可以是量化的分值。
再设权值向量为W=(w1,w2,…,wn),其中wi(i=1,2,…,n)表示因素xi(i=1,2,…,n)的重要程度,即分配给xi(i=1,2,…,n)的权重,满足
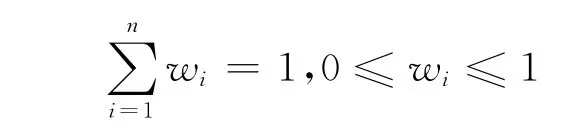
根据该师范大学所规定的综合测评的程序,综合测评由各班选出的评议代表构成的评议小组来进行。小组成员需要对各个评价因素进行模糊评价然后根据各指标统计评价级别的分布。假设对指标项xi评价为级别vj的评价人数占所有评测人数的比例为rij,那么判断矩阵为R=[rij]M×N。显然,该矩阵的每一行是对每个单因素的评价结果,整个矩阵包含了按评判结果集合V对评判因素集合X 进行评判所获的全部信息。

2.3 高校大学生综合素质评价的实例分析
现根据2.2节给出的模糊评判方法对该大学的学生综合素质进行评价。根据图1所示的综合素质评价体系表,组织由20名学生构成的评议小组对某位大学生进行评价,并根据德尔菲方法求得的各级指标对应的权重向量如下。
(1)一级评价因素的权重矩阵:
W=(w1,w2,w3,w4)=(0.15,0.65,0.1,0.1)
(2)二级评价因素的权重矩阵:
p1=(0.2,0.1,0.4,0.3),p2=(0.3,0.5,0.2),
p3=(0.3,0.4,0.3),p4=(0.6,0.4).
针对每个指标设定五个评价级数:v1优秀,v2良好,v3中等,v4及格,v5差,五个评语的分值分别是:
K=(95,85,75,60,45)。
针对二级评价指标项统计每个级别的分布,可得到如下的判断矩阵:
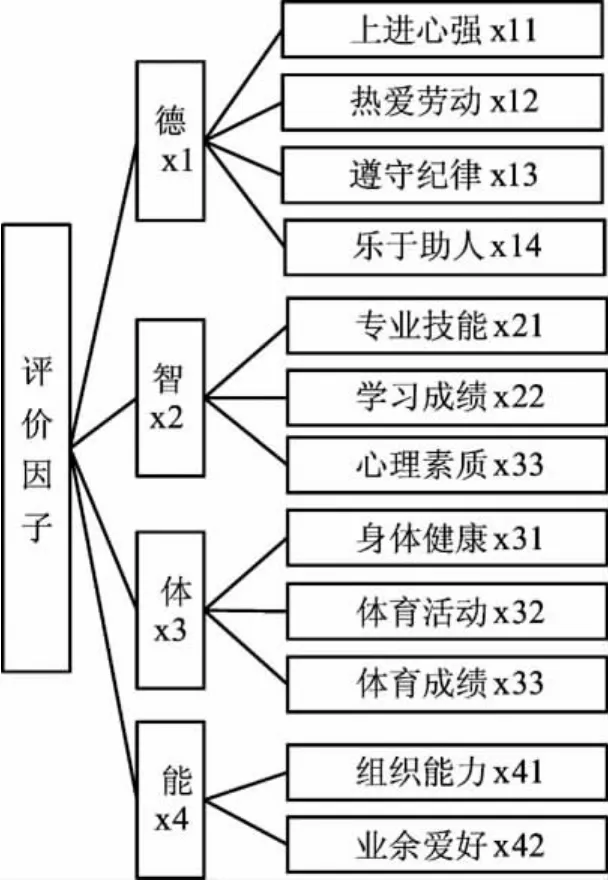
图1 大学生综合测评体系表



该结果表明:40.85%的人认为该学生综合素质优秀,31.55%的人认为该学生综合素质良好,21.35%的人认为综合素质中等,6.25%的人认为综合素质及格,无人认为该学生综合素质差。由获得的综合指标G,可得到该学生综合素质对应的成绩得分y=G·K=85.3875。从该例可以看出在对学生综合素质进行评价的过程中,需要对各项指标精确评分,这是一项严格的要求,只有经验丰富的专家才能做到,而一般的评测人员或许只能对某项指标做出“优”,“良”,“中”,“差”等模糊评判。如果引入神经网络的开放性,让网络自由地调整权值和阈值,可获得更好的效果。下面将人工神经网络理论应用于大学生综合素质评价,通过对已知样本的学习,获得评价专家的经验,知识,主观判断,及对目标重要性的权重协调能力,从而降低评价过程中人为因素的影响,较好的保证评价结果的客观性。
3 基于BP神经网络的大学生综合素质测评
BP神经网络结构简单、训练速度快且逼近精度较高,是目前实践中应用最为广泛的人工神经网络模型。该网络由一个输入层、若干个隐层和一个输出层组成,每层均有一个或多个神经元节点,信息从输入层依次经各隐层向输出层传递,层间的连接关系强弱由连接权来表征。通过样本集对网络的连接权进行学习和调整,以使得网络实现给定的输入输出映射关系,连接权的调整采用的是反向传播学习算法,即BP算法[1]。下面具体介绍BP神经网络模型的结构和算法。
3.1 BP神经网络方法及结构
根据大学生综合素质评价过程的要求,以二级评价指标作为神经网络的输入构造三层BP神经网络,网络输入层神经元共12个,每个神经元对应一个评价指标,其输入为评价指标得分。隐层神经元若干,输出层有一个神经元,代表通过综合评价得出的分数,即综合素质得分。
在Matlab软件平台下神经网络模型的程序实现简单易用,既可以采用程序文件来精确控制网络的训练参数也可以使用图形化的界面来完成神经网络的构建和训练。在Matlab中建立BP神经网络主要有三个参数:神经网络层数,每层神经元的个数及传递函数形式。
对于前向型神经网络的结构设计,其隐层神经元个数的选择是一个非常复杂的问题,隐层单元个数与问题的要求以及输入输出单元个数有直接的关系,隐层单元过多将会导致神经网络训练时间过长、误差不易控制及容错性差等问题。所以隐层单元个数选择经常需要根据设计者的经验和多次实验来确定,不存在一个理想的解析式。
对于非线性函数逼近问题,网络的隐含层神经元的传递函数可选择S型正切函数,输出神经元的传递函数选择S型对数函数,输出量为0到1之间,此时网络可以实现从输入到输出的任意非线性映射。
3.2 BP神经网络仿真
1)数据采集。利用文章第2部分中得到的数据作为神经网络的训练数据,网络的输入数据可以表示为:Date=[RT1,RT2,RT3,RT4]T。输出目标数据为:G=(0.4085 0.3155 0.2135 0.0625 0)。
2)网络训练。可以根据确定隐层单元数目的如下两个参考公式:

暂时确定网络隐层神经元个数为n1∈[4,7],在Matlab中利用如下命令

即可对网络进行训练和仿真。还可以借助Matlab神经网络工具箱提供的图形化界面来完成神经网络的训练和仿真过程。使用命令“nntool”打开神经网络工具箱中提供的图形化界面,其中包括输入数据和输出数据的选择窗口,界面下方的新建按钮可以方便地帮助建立神经网络模型,可以调节网络类型,输入和输出数据、学习函数,网络层数、激活函数等相关参数。
在实际仿真训练过程中,通过调节隐层神经元个数可以试验出不同的网络收敛速度和训练精度,由于每次仿真结果都不相同,表现出一定的随机性,不便于对仿真所得到的BP神经网络的选择和应用。Matlab软件提供了强大的Simulink工具可以帮助调节特定神经网络中的各种参数,并且实现起来非常方便。本例中利用“gensim()”命令可以将训练出来的BP网络转化为Simulink仿真模型。在Simulink中利用可视化界面查看和编辑网络的各种参数,如权值、偏置向量和激活函数等,调节该网络的权值可以使网络输出与期望输出之间的误差更小。因此本文引用Matlab所提供的Simulink仿真平台来建立神经网络,保存便于应用的仿真模块,方便结果的共享。
利用专家给出的评测结果对网络进行训练,选取误差相对较小的训练结果来生成Simulink模块,本文根据多次仿真实验的对比,选择隐层元素为6的神经网络来构建Simulink仿真模块如图2所示,由于神经网络模型的特性,仿真结果并不一定会和目标数据完全相同,其间会有一些误差,利用Simulink模块可以根据目标数据的要求修改网络参数,如权值,偏置量等,使其有更加合理的输出。
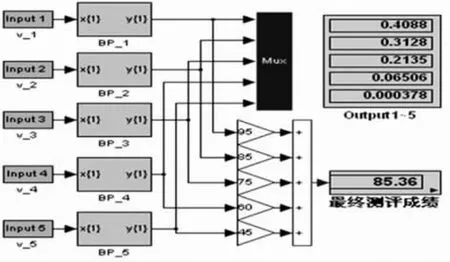
图2 根据训练结果生成的Simulink模块
本例采用一种简单增加网络输出的方式,即在网络输出端根据期望输出加上合适的常数,这种方式简单易行,比修正网络的各层权值参数更快捷,如图3,图4为逐级打开网络结构的Simulink模块的情形。
调节权值和偏置量的取值可以使得网络的最终输出和目标值误差最小。

图3 神经网络子模块的展开

图4 神经网络模块的结构和权值窗口
3.3 网络测试及结果分析
利用已经训练好的神经网络模块,在Simulink环境下对网络进行数据仿真,利用随机数发生器生成多组输入向量,为了使输入向量符合输入数据的实际意义,需将这些随机向量进行归一化处理,并由规范化函数转化为神经网络的输入数据。对网络所映射出的结果进行归一化处理即可得到一组网络输出。
首先将大学生综合素质评价方法设计中的样本X输入网络,网络得出该同学的综合素质得分为85.36,与模糊评判结果85.3875的相对误差绝对值为0.0322%,说明经过微调之后的神经网络模块在仿真精度上能够满足要求。随机利用50个样本对对网络进行仿真,并利用模糊评判规则对这50组数据进行评价。比较神经网络的映射结果和模糊评判结论之间的误差,发现其与模糊评判多数结果的误差保持在0.3%以内,但是对于输入数据不规范的情况,网络输出会出现问题,在实际应用中,对学生综合素质评测的输入数据一般是经过人工整理的,比随机数据更加规范,因此我们一般将重点放在提高网络仿真精度上,对于不规则数据的筛选是将来进一步设计要考虑的问题。
考虑到实际应用过程中输入数据一般是符合特定结构特征的,我们认为神经网络模型在大学生综合素质测评中有一定的可靠性,且形成模块后输入和输出都比较简单,整个过程不需要相关专业知识,加上精度比较高因而利于推广和应用。
4 结束语
相较于模糊综合评价常见的主观、客观确定权重的方法,神经网络具有一定的优势.它克服了人为和随机因素的干扰,并且可以应用于指标之间因为互相影响而呈现出非线性关系的情况,因此利用模糊评判结果训练的三层BP神经网络能够精确地模拟模糊评判的结果。基于BP神经网络构造的综合评判模型使模糊评判具有了自学习的能力,模型具有比模糊评判模型更开放,更灵活的特点,可以降低评价过程的主观性和随意性,使大学生综合素质评价更好地体现客观性、公正性和科学性,其运行效率和精度均能满足实用要求。随着软件技术的发展,利用Matlab的神经网络工具箱来建立、训练并分析神经网络使得神经网络的应用更加便利,实用性更强。本文结果不仅可以用于大学生综合素质评价也可以用于其它复杂非线性映射的建模,具有较广泛的实用性。
[1] 周世官,苏日娜.模糊神经网络在课堂教学质量评价中的应用[J].计算机仿真,2008,5:287-289.
[2] 程树林,程玉胜.模糊综合评判通用仿真软件的设计与实现[J].计算机工程,2010,33(3):51-54.
[3] 杨根兴,高大启,宋国新.基于神经网络的软件质量综合评价方法[J].华东理工大学学报,2004,30(6):292-295.
[4] 商姚,林红,晏启祥.以模糊评判为基础的大学生素质BP神经网络模型[J].西华大学学报,2005,6(3):87-89.
[5] 秦荪涛.高校教学工作水平评估的人工神经网络模型[J].计算机系统应用,2004,(10):34-37.
[6] 飞思科技产品研发中心.神经网络与 MATLAB7实现[M].第1版(北京:电子工业出版社),2005:99-108.
[7] 李翔,苏成,王韶君.基于模糊神经网络的综合评判方法[J].计算机工程,2009,35(6):200-201.
Neural Networks Model of Evaluation of Comprehensive Quality and Simulink Implementation
WANG Ning, SUN Xiao-ling, LIANG Yan(Department of Mathematics,Hefei Normal University,Hefei 230601,China)
Aiming at the existence of many non-quantitative factor and the nonlinear characteristics of evaluating the comprehensive quality of college students,a BP neural network model of evaluation has been built in this paper.The measured function has been approximated by using BP neural network.The proposed model has a higher efficiency than that of existing evaluation system,and can be generalized to produce modularized programs.The method of simulating calculation of BP neural network has strong operability.Owing to no need of complex operation during fuzzy evaluation,the method has wide practicability.
BP neural network;fuzzy complex judgment;evaluation of comprehensive quality
TP183.
A
1674-2273(2011)06-0015-05
2011-05-10
安徽省省级自然科学研究项目(NO.KJ2009B148Z);安徽省高等学校优秀青年人才基金项目(NO.2009SQRZ157,NO.2009SQRZ156)
王宁(1978-),男、讲师,硕士,主要研究领域为神经网络,计算机仿真技术;孙晓玲(1977-),女,讲师,硕士;梁艳(1981-),女,讲师,硕士。

