抛物线方程算法在不规则地形电波传播中的应用

孔 勐， 王驰骏， 胡金花， 时晶晶， 李雯雯

（1．合肥师范学院 物理与电子工程系，安徽 合肥 230601；2．电子科学技术大学 微电子与固体电子学院，四川 成都 611731）

抛物线方程算法在不规则地形电波传播中的应用

孔 勐1， 王驰骏2， 胡金花1， 时晶晶1， 李雯雯1

（1．合肥师范学院 物理与电子工程系，安徽 合肥 230601；2．电子科学技术大学 微电子与固体电子学院，四川 成都 611731）

文章对标准抛物线方程（SPE）的分裂步傅里叶变换（SSFT）方法进行了详细的分析，引入一种适合SPE的不规则地形建模方式，利用SSFT算法计算自由空间与不规则地形的电波传播问题，与经典理论计算所得的结果相当吻合。

抛物线方程；分裂歩傅里叶变换；不规则地形；电波传播

抛物线方程（Parabolic Equation）首先是由Lenontovich［1］和 Fock［2］在20世纪40年代提出，PE方法初期主要用来处理比较复杂的声波的传播和光学等方面的问题。PE方法广泛用于计算各种波的传播问题，对长距离声波在海洋中的传播和地震波传播的计算和研究提供了一种有效、准确的方法［3，4］。近年来，国内外学者开始将抛物线方程方法应用于处理电波传播与电磁散射问题［5，6］。文章针对标准抛物线方程（SPE）采用分裂步傅里叶变换（SSFT）算法求解。该方法首先对SPE进行傅里叶变换，使原来空间域的SPE变成更为简单的频域SPE，解较为简单的频域SPE，然后对解得的结果进行傅里叶逆变换，使频域解还原为空间域解。在步进求解SPE时，SSFT的步长几乎不受波长的限制，可以取很大。因此，对于大尺度电波传播的问题，SSFT算法求解速度快，稳定性好。

1 抛物线方程的SSFT算法分析

1．1 数值解法

设与水平面成α角方向传播的平面波波函数为：

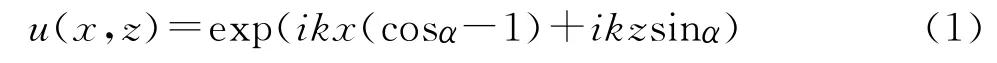
对u（x，z）进行傅里叶变换，得到频域波函数U（x，f）为：

其中n为折射系数。

SPE解的形式为：

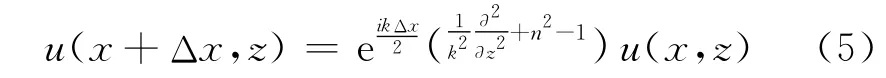
对（5）式两边进行傅里叶变换及逆变换得到一般解的形式为：

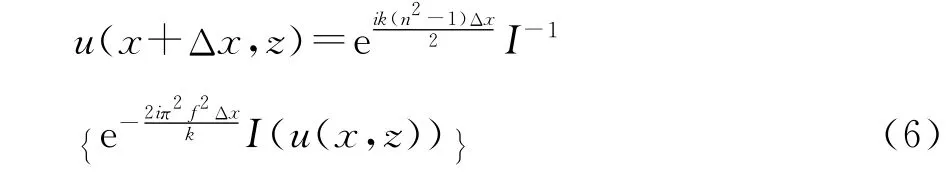
由（6）式可以看出：任何一个面的场值都可以通过上一个面的场值递推计算得到，其中Δx为递进步长。

1．2 初始场的设置

通过对发射天线的方向图函数进行傅里叶变换来求得PE的初始场，得到PE在二维均匀无界空间中的初始场分布，再利用几何光学（GO）中的双射线模型将无界空间中的初始场分布转换成地表以上半空间中的场分布，从而最终得到所需的PE初始场。

假设反射天线方向图函数为A（z），SPE上半空间的初始场分布为：

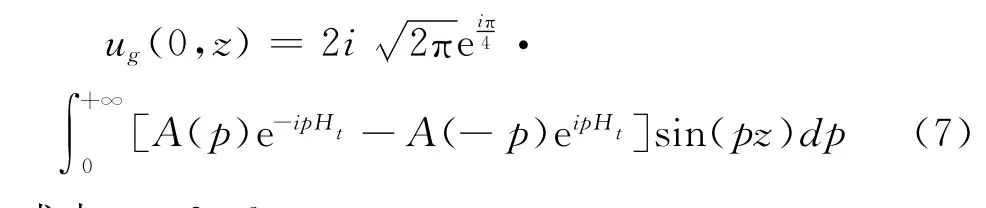
式中p＝2πf

通常采用的高斯方向图为：

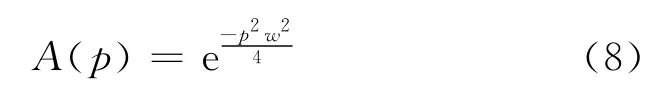
图1所示频率为300MHz，Ht＝12．5不同极化方式下初始场的归一化幅度值。

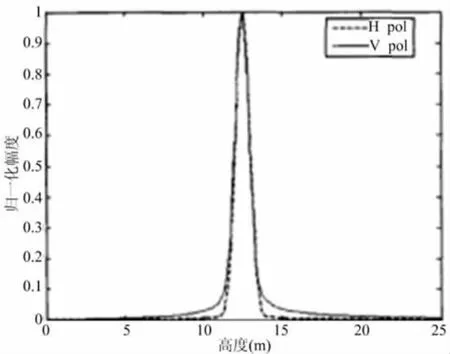
图1 初始场的归一化幅度值

1．3 边界条件

SPE模型只考虑电波的前向传播，构成这个区域的边界主要为上方的吸收边界和下方的地表边界以及左边的起始边界（初始场分布），在传播方向上计算域的边界是开放的。SPE模型的计算域及其边界如图2所示。

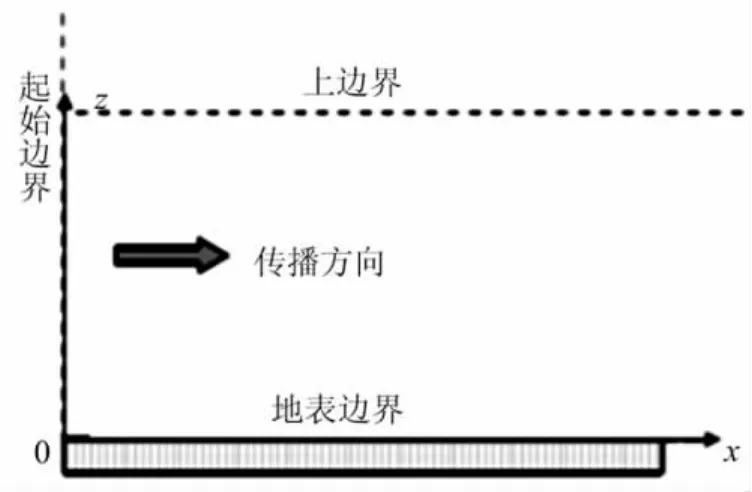
图2 SPE模型的计算域及其边界

SPE模型的上边界是个吸收边界，主要用来截断SSFT的计算域。从初始距离处开始，z方向上的每一步进场量都乘以Cosine-taper（Tukey）窗函数（9）式，以满足Sommerfeld辐射条件。

其中，zmax为计算域的最大高度。

假设地表近似为理想导体平面，将边界条件应用到傅里叶变换式中，可得水平极化条件下正弦变换S形式为：

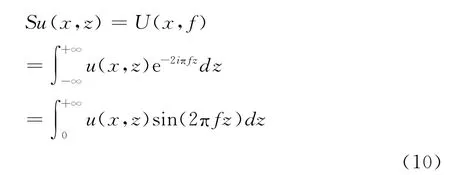
SSFT算法在结合地表面边界条件后解的形式为：

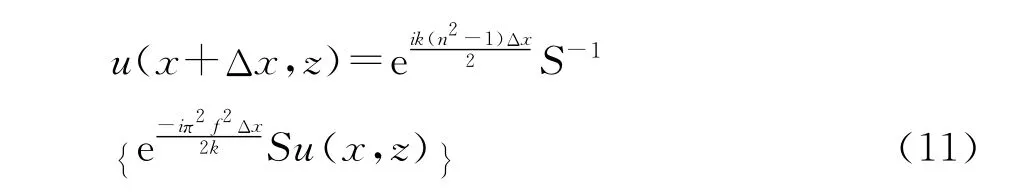
其中S－1＝4S［7］。

2 不规则地形的建模

文章采用由Beilis和Tappert提出的连续移位变换模型［8］，结合SSFT算法应用到不规则地形的电波传播中。其主要思想是在整个计算域的地形剖面上新建一个坐标系，通过坐标变换将不规则地形上的PE转换成平面地表上的形式，坐标（x，z）为如图3所示的原坐标系。

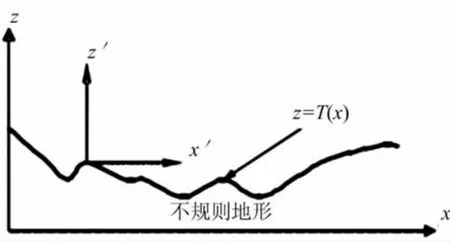
图3 原坐标系（x，z）和新坐标系（x′，z′）的关系图

在原坐标系中，假设地形的高度由下面的函数确定：

要使地形变得“平坦”就需引入相应的坐标变换，方法如下：

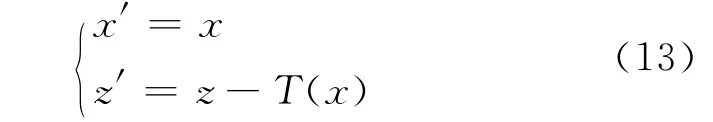
坐标变化后，可得到在新坐标下SPE形式：

在新的坐标中，令v（x′，z′）＝eiθ（x′，z′）u（x，z），其中θ为待变量［9］，其中修正折射指数：

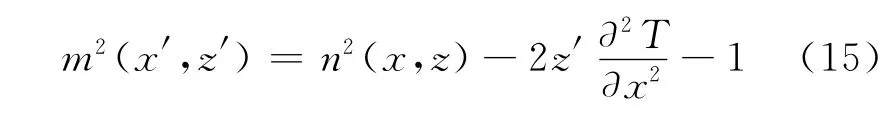
连续移位变换地形模型具有很好的通用性，只要地形起伏特征可以用一个存在x二阶的连续函数来描述，在这种地形模型上，SPE本身的形式不变，只是将原先的折射指数项n2用m2代替，因此结合式（11），即可求解不规则地形的电波传播问题。

3 计算实例

真空中（折射系数n＝1），频率为0．3GHz的平面波ψ＝exp（ik（x cos（α）＋z sin（α））），入射角α＝10°，计算尺度为5000m。利用SSFT方法计算该问题，步长取200m，计算时间为0．34s，将场值u（x，z）（x＝5000m）的实部和虚部的计算值与解析解进行比较，其结果如图4、图5所示。图中可以看出，SSFT方法与解析解的结果吻合较好。由于计算量大，PE的有限差分（FD）方法［10］在保证精度的基础上根本无法完成计算。

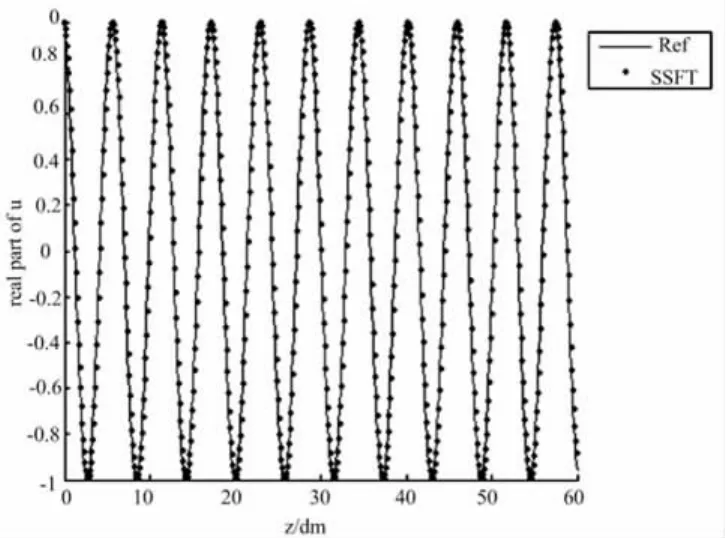
图4 SSFT方法计算真空中电波传播的场值实部

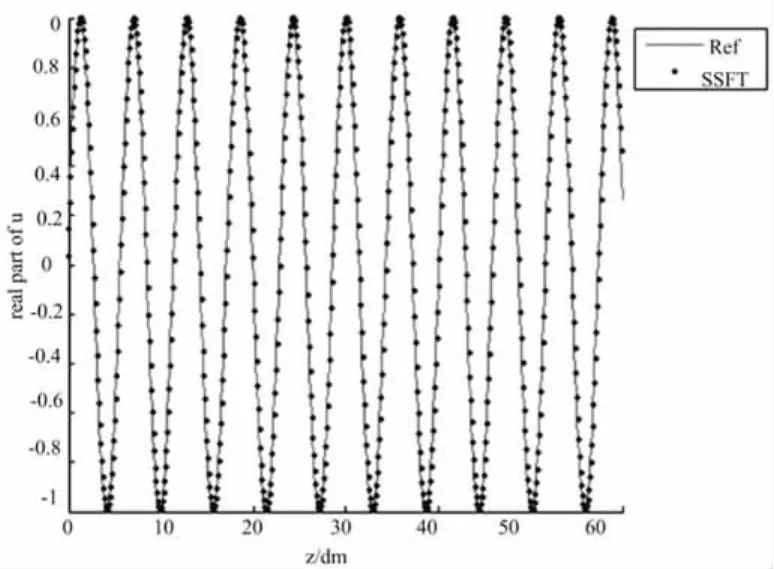
图5 SSFT方法计算真空中电波传播的场值虚部

下面通过仿真来验证该方法对不规则地形电波传播问题的有效性。考虑电磁波在一个类似正弦包络形状的不规则地形上传播，其中，地形函数为：

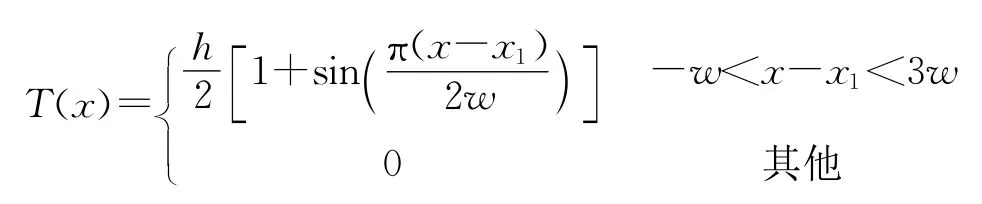
式中，h为顶点高度，x1为包络半高程所在的距离，w为包络的半宽度。设h＝229m，x1＝15km，w＝10km。发射天线高度为Ht＝30m，频率为f＝3．0GHz，高斯方向图3d B宽度为θbw＝3°，电波水平极化。假设大气为真空，折射系数n＝1，大地为良导体。在水平方向上使用迭代的步长Δx＝100m，计算至50km处。图6显示了本文的计算结果。

从计算结果可以看出，面向辐射源的一面有很强的反射，而在背面有很深的阴影区，在阴影区的场强显著下降至－70dB。这与文献［11］中的图2基本一致，证明了该方法的有效性。

图6 SSFT计算不规则地形的电波传播幅度值

4 结束语

文章推导出SPE的SSFT算法一般解的公式，结合SSFT方法的初始场和边界条件设置，引入一种适合SPE的不规则地形建模方式，利用SSFT算法计算自由空间和不规则地形的电波传播问题，得到良好的效果，证明了SSFT算法在计算大尺度不规则地形的电波传播问题的有效性。

［1］ Leontovich M A，Fock V A．Solution of propagation of electromagnetic waves along the Earth’s surface by the method of parabolic equation［J］．J Phys USSR，1946，10（1）：13-23．

［2］ Fock V A．Electromagnetic Diffraction and propagation Problems［M］．London：Pergamon Press，1965：213-234．

［3］ Dalrymple R A，Martin P A．Perfect boundary condition for parabolic water－wave models［J］．proc．R．Soc．London A，1992，437（1899）：41-54．

［4］ Collino F，Joly P．Splitting of operators，alternate directions and paraxial approximations for the three－dimensional wave equation［J］．SIAM J．Sci．Comput，1995，16（5）：1019-1048．

［5］ Zaporozhets A A，Levy M F．Bistatic RCS calculations with the vector parabolic equation method［J］．IEEE Trans on AP，1999，47（11）：1688-1696．

［6］ 胡绘斌，毛钧杰，柴舜连．电波传播中求解宽角抛物线方程的误差分析［J］．电波科学学报，2006，21（2）：199-－202．

［7］ Levy M F．Parabolic Equation methods for electromagnetic wave propagation［M］．London：The Institution of Electrical Engineers，2000：23-46．

［8］ Beilis A，Tappert F D．Coupled mode analysis of multiple rough surface scattering［J］．Acoust Soc Amer，1979，66（3）：811-826．

［9］ Barrios A E．A terrain parabolic equation model for propagation in the troposphere［J］．IEEE Trans on AP，1994，42（1）：90-98．

［10］ 孔勐，吴先良，黄志祥．基于SSP抛物线方程方法计算电磁散射问题［J］．合肥工业大学学报（自然科学版），2009，32（11）：1773-1775．

［11］ Donohue D J，Kuttler J R．Propagation modeling over terrain using the parabolic wave equation［J］．IEEE Trans on AP，2000，48（2）：260-277．

Application of Parabolic Equation Method to Radio Propagation over Irregular Terrain

KONG Meng1， WANG Chi-jun2， HU Jin-hua1， SHI Jing－jing1， LI Wen-wen1（1．Dept．of physics and Electronic Engineering，Hefei Normal University，Hefei 230601，China；2．School of Microelectronics and Soild-state Electronics，University of Electronic Science and Technology of China，Chendu 611731，China）

Standard parabolic equation （SPE）with Slip-step Fourier Transform （SSFT）method and SPE modelling of radio propagation over irregular terrain are elaborated．To work out radio propagation in vacuum and radio propagation over irregular terrain with SSFT method is identical to the results available by the classical method．

parabolic equation；Slip-step Fourier Transform；irregular terrain；radio propagation

O451

B

1674-2273（2011）06-0031-04

2011－01－20

1．安徽省教育厅自然科学基金重点资助项目 （KJ2010A283）；2．合肥师范学院院级自然科学基金资助项目 （2010kj09）．3．合肥师范学院重点科研基地研究专项资助项目（2011jd06）

孔勐（1983－），男，安徽亳州人，合肥师范学院物理与电子工程系教师，硕士，主要研究方向：无线通信与电磁兼容、电磁场数值方法。