负反馈放大电路稳定性的仿真分析与研究

杨一军， 陈得宝， 邹 锋， 王孟杰， 方振国， 李 峥

（淮北师范大学 物理与电子信息学院，安徽 淮北 235000）

负反馈放大电路稳定性的仿真分析与研究

杨一军， 陈得宝， 邹 锋， 王孟杰， 方振国， 李 峥

（淮北师范大学 物理与电子信息学院，安徽 淮北 235000）

对两级电压串联负反馈放大电路的相对稳定性，分别采用了微分形式、差分形式，以及所推导的适用于反馈系数变化条件下的普遍公式进行了分析。结果表明：基本放大器增益变化ΔA不大时，微分形式与差分形式计算结果基本一致；反馈系数改变时，仅有所推公式成立；若ΔA也较大，三种计算结果可以相差很大。另外即使ΔA＝0，由反馈系数的变化也能形成较大反馈放大器增益的相对变化。

负反馈；反馈系数；稳定性

1 引 言

对于负反馈放大电路的分析，常采用方框图分析法，获得基本放大器增益后，进而可以得到反馈放大器性能指标，近年来不断出现该方面的报道［1－2］，引起了人们的关注。但关于反馈系数变化后增益的相对稳定性讨论，至今尚未见到。本文用理想运算放大器组成二级电压串联负反馈放大电路，推导了适用于反馈系数变化下的相对稳定性公式，在方框图分析方法的基础上，编写MATLAB程序计算了（1）反馈系数F不变、基本放大器A变化；（2）F变化、同时A变化；（3）F改变、A保持不变几种情况下反馈放大器增益的相对稳定性，结果完全符合所推公式。

2 理论计算与仿真

2．1 电路的基本构成

负反馈放大电路如图1所示。经判别知：当联动电键S1、S2接M 点，图1电路为反馈放大器；接N点则是考虑反馈网络负载效应后的基本放大器。

2．2 源电压增益

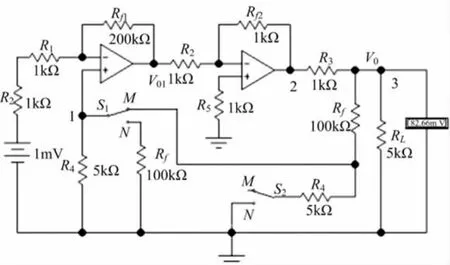
图1 电压串联负反馈放大电路

取电阻单位kΩ，电压单位m V，编写 MATLAB程序如下

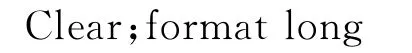
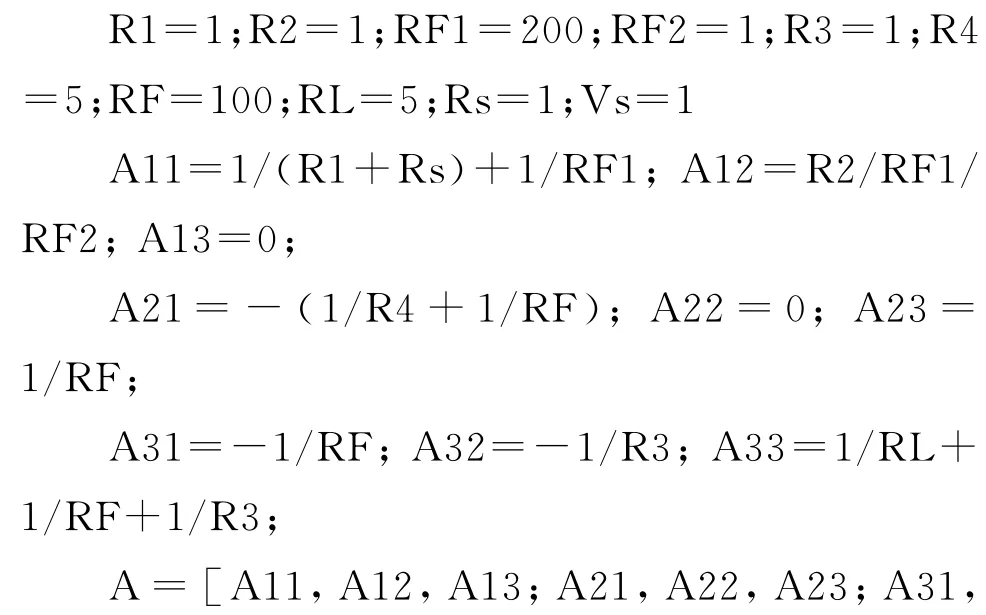
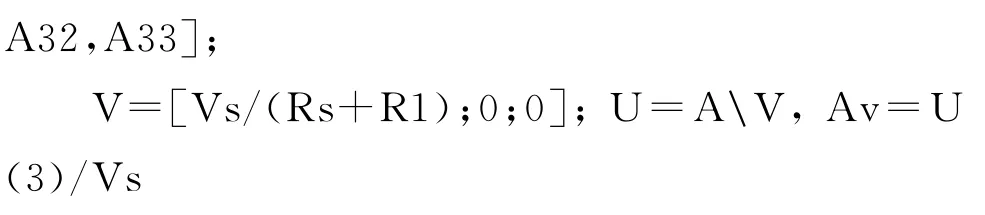
运行得 V3＝16．614m V，则 Avvsf＝16．614，与利用式（2）计算有0．879%的相对误差，这是方框图分析法略去网络直通效应所造成［3］。

另外，启动EWB仿真，我们看到其结果与理论计算非常接近，这是计算和仿真中所采用的元器件为理想模型所致。

表1 理论计算与仿真结果

2．3 相对稳定性计算

关于负反馈放大器的相对稳定性讨论，当基本放大器A变化是小量时，相应的微分形式为［4］

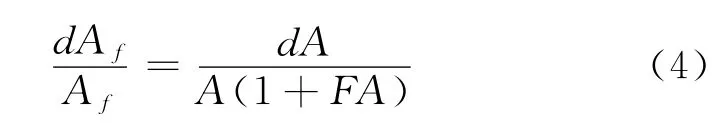
该公式推导利用了微分性质，反映了反馈放大器增益的相对稳定性。当条件不满足时，文献给出差分形式［5］

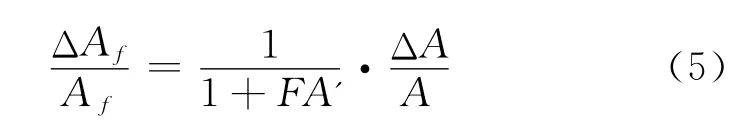
其中A′为变化后的基本放大器增益，gΔA＝A′－A，Af＝Af′－Af（Af′g 为变化后的反馈放大器增益）。比较式（4）与式（5）可知，略去基本放大器增益变化前后的差异，两者相同。然而与式（4）一样，式（5）也没有涉及反馈系数F的变化。当其变化时，用F′表示变化后的反馈系数，用ΔF＝F′－F表示其变化量，有

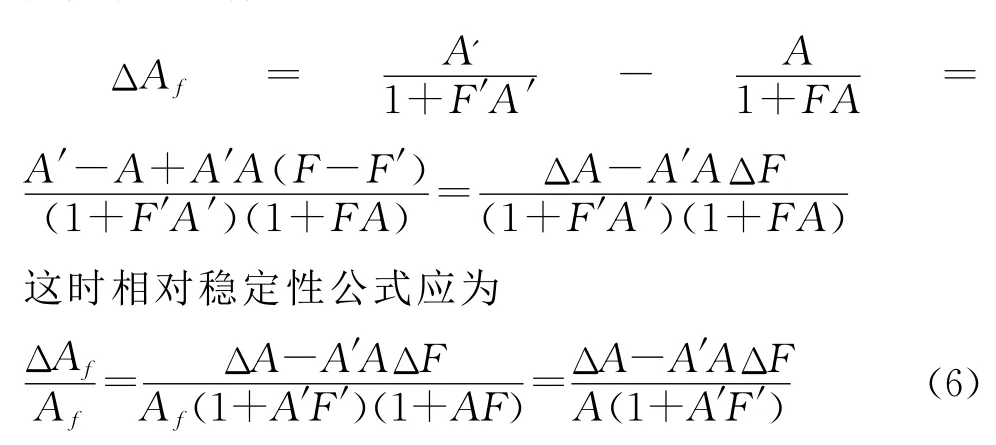
可以看到，与式（4）、式（5）明显不同，即使基本放大器增益没有变化gΔA＝0，但反馈系数的变化也引起反馈放大器增益的变化，即ΔAf≠0。

保持Rf2不变，改变Rf1、Rf或R4，运行 MATLAB程序，计算得变化后的基本放大器增益Avvs′和反馈放大器增益Avvfs′，具体见表2（电路参数改变前Avvs＝82．677，Avvfs＝16．614，Fvv＝R4／（R4＋Rf）＝0．047619）。

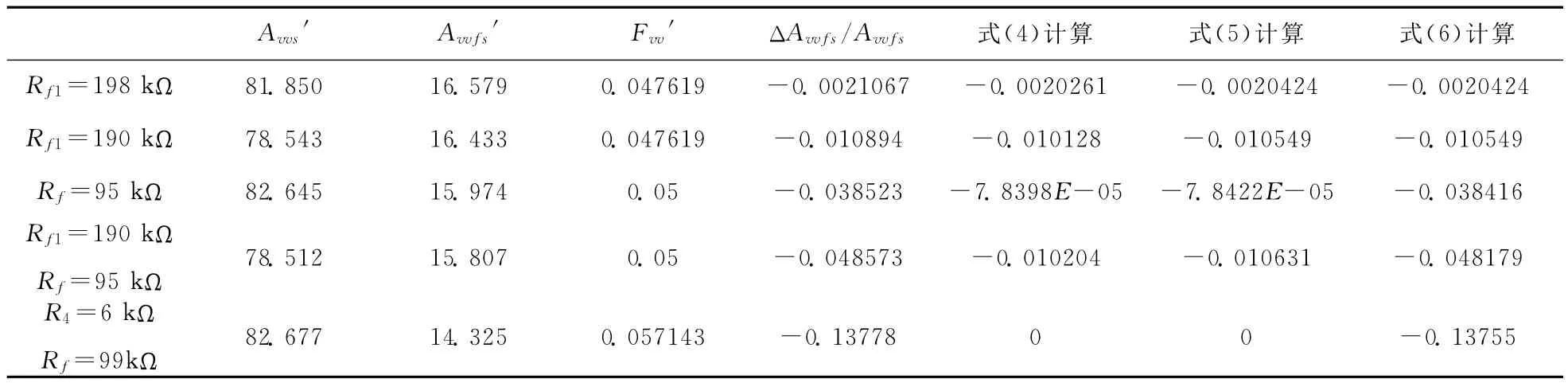
表2 不同计算公式下相对反馈放大器增益相对稳定性

2．4 讨论

（1）A 变化不大时，式（4）、式（5）结果相差不大（第2行），与第5列的标准值ΔAvvfs／Avvfs分别有3．98%和3．15%的相对误差，为工程计算所允许。同时因反馈系数不变，式（6）退化为式（5），二者计算结果相同（第2、3行）。

（2）随A 变化增大，式（4）、式（5）间差别明显增大（第3行），与标准值分别有7．57%和3．28%的相对误差，说明式（4）已经不适用。

（3）反馈系数改变时，可以看到仅有式（6）与标准值一致（第4行），表明式（4）、（5）已经不适用。同时因ΔA较小，式（4）、（5）计算结果仍相差很小。说明只要基本放大器增益变化不大，用式（4）或式（5）的计算都不会带来明显差异。

（4）当A和F同时变化时，若ΔA较大，则三个公式计算结果各不相同，差别较大（第5行）。

（5）取Rf＝99kΩ，R4＝6kΩ，根据式（1）知，A 不变，式（4）、（5）计算结果都是0，但式（6）计算结果为－0．13755（第6行），说明了反馈系数改变对反馈放大器相对稳定性的影响。

（6）在各种情况下，式（6）与标准值非常贴近，说明式（6）是一个普遍成立的公式。同时，以上结论对各种类型的负反馈放大器都适用，具有普遍意义。

3 结束语

利用推导的负反馈放大电路中反馈系数变化时反馈放大器增益相对变化的稳定性公式，对由理想运算放大器组成的二级电压串联负反馈放大电路进行分析。经运行MATLAB程序，得到的计算结果表明，微分形式与差分形式的相对稳定性公式仅在满足一些特定条件下成立，而反馈系数改变下的相对稳定性公式则满足各种情况，是一个普遍适用的公式。

［1］ 艾永乐，李端．反馈判断及负反馈性能仿真探讨［J］．北京电子科技学院学报，2008，16（2）：23-25．

［2］ 杨一军，王欣．基于EWB的负反馈放大电路的方框图分析［J］．电气电子教学学报，2007，29（6）：24-26．

［3］ 谢嘉奎主编．电子线路（线性部分 第3版）［M］．高等教育出版社，1988．

［4］ 童诗白，华成英．模拟电子技术基础（第4版）［M］．高等教育出版社，2006．

［5］ 朱光琳，陈谋文．负反馈提高放大倍数稳定性的分析［J］．湛江师范学院学报（自然科学版），1999，20（2）：46-48．

The Simulation Analysis and Investigation of Negative Feedback Amplifier’s Stability

YANG Yi-jun， CHEN De-bao， ZOU Feng， WANG Meng－jie， FANG Zheng－guo， LI Zheng（School of Physics and Electronic Information，Huaibei Normal University，Huaibei 235000，China）

The relative stability of negative feedback circuit with two-staged voltage series is analyzed with differential，deviation and general formulation under the condition that the feedback coefficient is changing．The results indicated that solutions for types of differential and deviation are almost identical with little change of A gain，only the deduced formulation is confirmed when the feedback coefficient is changed and the three formulations are in large difference when A gain is large simultaneously．In addition，the change of feedback coefficient can form the relative change of feedback amplifier with large gain．

negative feedback；feedback coefficient；stability

TM13；TM391．9

A

1674-2273（2011）06-0035-03

2011－03－10

安徽省教育厅重点资助项目（20100508），淮北师范大学资助项目（jy10233）

杨一军（1956－），淮北师范大学物理系教授，研究方向：电子技术。