用简并微扰法分析金属晶体中散射波较强情况
孟 影, 张晓森, 汪月琴
(安徽理工大学理学院,安徽淮南 232001)
用简并微扰法分析金属晶体中散射波较强情况
孟 影, 张晓森, 汪月琴
(安徽理工大学理学院,安徽淮南 232001)
在一维晶格中,若电子波矢k落在布里渊区边界k=±(nπ/a)时,电子将遭受到与布里渊区边界平行的晶面族的反射,由于在布里渊区边界散射波很强,满足布拉格全反射的条件,此时微扰论不再适用,须用简并微扰法来处理电子的能带分布。
简并微扰法;布里渊区;散射波;禁带宽度
1 微扰计算
所谓简并微扰法,是指在周期场中运动的电子原有若干状态能量相同,在零级微扰计算中,根据波动方程求得这些简并态之间的适当线性组合,其它能量不同的状态,在进一步近似中考虑[1-3]。
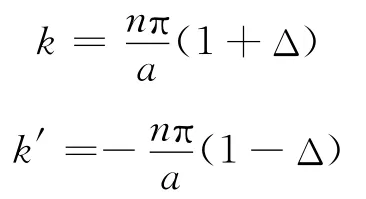
则,零级波函数可以写成是前进波,

将此波函数带入薛定谔方程,
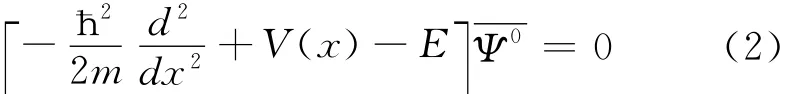
将(1)代入(2),并考虑V(x)=V0+ΔV,其中V0代表金属晶体周期势场的平均势,ΔV代表微扰势。得
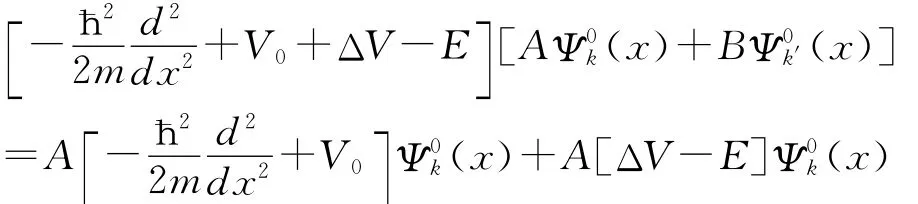

上式左乘(x),然后对dx积分,得

A、B有非零解的条件,即(x)存在的条件是(4)、(5)系数行列式为零。

2 讨论分析
(1)当Δ=0时,E=Tn±|V n|

(2)当Δ≠0,同时假定TnΔ≪|V n|<T n

两个相互影响的状态与微扰后,能量为E+和E-,态的原来能量较高,微扰使它上升,态的原来能量较低,微扰使它下降。

此结果与非简并微扰论一致[5]。
k和k′相互影响的结果,使原来能量较高的k态提高,原来能量较低的k′态下压。这是量子力学的普遍结果,在微扰论作用下相互影响的两个能级,总是原来较高的能量提高了,原来能量较低的能量下降。有人形象地比喻能级间的“排斥作用”[3]。
3 小结
金属晶体是空间点阵结构,计算金属中电子的能带分布有许多方法,当考虑电子波矢k落在布里渊区边界上,散射较强时,简并微扰是一种比较好的方法。微扰计算时,只需要计入能量相等(或相近)的两个状态之间的相互影响,这就是简并微扰的情况,微扰的结果是原来能级较高的更高了,原来能级较低的向下降。
[1] 黄昆,固体物理学[M].北京:高等教育出版社,2003:157-171.
[2] 王矜奉,固体物理教程[M].山东:山东大学出版社,2004:187-192.
[3] 郑文礼.用简并微扰法计算金属晶体电子的能带分析[J].承德民族师专学报,2001,21(2):32-34.
[4] C.基泰尔.固体物理导论[M].北京:科学出版社,1979:204-208.
[5] 方俊鑫,陆栋.固体物理学(上册)[M].上海:上海科学技术出版社,1980:209-217.
Degenerate Perturbation Theory Analysis The Strong Scattered Wave in Metal Crystal
MENG Ying, ZHANG Xiao-sen, WANG Yue-qin
(Schoolofsciences,AnhuiUniversityofScienceandTechnology,Huainan232001,China)
If electronic wave vector drops on brillouin zone boundary of one-dimensional crystal lattice,electron will suffer to the reflection of crystal plane family which is parallel to brillouin zone boundary.Because brillouin zone boundary scattered wave is very strong,which meets the conditions of bragg total reflection.at this time,perturbation theory is no longer suitable,and degenerate perturbation theory is used to dealing with electronic band distribution.
degenerate perturbation theory;brillouin zone;scattered wave;band gap
O471.5
A
1674-2273(2011)06-0029-03
2011-07-10
孟影(1977-),女,安徽阜阳人,工学硕士,安徽理工大学理学院讲师,研究方向:巨磁阻薄膜。

