基于布里渊散射的光纤温度和应变快速感知

官国飞，宋庆武，陈志明，钟巍峰，李 军

(江苏方天电力技术有限公司，南京 211103)

0 引 言

目前，物联网[1]正在如火如荼开展。传感器构成了物联网的基础，尤其是分布式光纤传感器[2-3]，基于单根光纤即可测量光纤沿线的物理场数据，在大型设备和结构，如铁路、大桥、输油管道和输电线路等的状态监测中应用非常广泛[4-7]。基于布里渊散射的分布式光纤传感的解调方法是通过计算布里渊频移来实现的[8]。计算布里渊频移最为常见的方法是拟合方法。当假设布里渊谱满足洛伦兹[9]、高斯或伪Voigt模型[10-11]时，对应的优化问题属于非线性最小二乘问题，对应的优化算法准确性较高，但计算量较大，影响了温度和应变解调的实时性。抛物线拟合方法[12-13]中对应的优化问题属于线性最小二乘问题，无需迭代即可快速计算最优解。但该方法存在的问题是准确性受布里渊谱的扫频范围围绕布里渊频移对称程度的影响较大，需要研究加以改进。

为了解决该问题，基于光纤沿线布里渊频移波动的布里渊谱，比较了本文基于抛物线和伪Voigt模型拟合方法的准确性和计算速度，指出了原始抛物线拟合方法存在的问题。在此基础上提出了采用Savitzky-Golay滤波[14]得到较为准确布里渊频移后截取对称扫频范围布里渊谱的改进抛物线拟合方法，研究了Savitzky-Golay滤波中多项式阶数和滤波窗长对滤波效果的影响，确定了最佳多项式阶数和滤波窗长。基于光纤沿线温度或应变变化的布里渊谱，采用原始抛物线和伪Voigt模型拟合方法与改进的抛物线拟合方法的比较验证了所提方法的有效性。

1 基于布里渊散射的分布式光纤传感

基于布里渊散射的分布式光纤传感中，通常来说入射的光为脉冲光，这样通常认为测量得到的布里渊谱近似服从伪Voigt模型[10]，表示如下：

式中：gB为布里渊增益；v为频率；vB为布里渊频移；ΔvB为线宽；g01和g02分别为洛伦兹和高斯模型布里渊增益峰值。可以通过优化如下的目标函数来得到布里渊频移的最优估计：

式中：E为误差的平方和；vn、gBn和en分别为第n个频率值、该频率值对应的布里渊增益及误差；N为扫频点数。通过优化算法可使E趋于最小化，此时对应的vB即为提取得到的布里渊频移。以上方法通常称为基于伪Voigt模型的拟合方法，其优势是能充分利用伪Voigt模型表征不同入射光脉宽下布里渊谱形状的优势，抗干扰能力比较强，但由于多次迭代才可使目标函数趋于最小值，计算耗时较长，影响了基于布里渊散射分布式光纤传感系统的实时性。

当光纤受到温度和应变作用后，其布里渊谱峰值对应的频率即布里渊频移会发生变化，满足如下关系[2]：

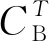
若光纤上的布里渊频移改变仅由温度或应变单一物理量导致，则温度和应变的解调公式为

因此，根据提取的布里渊频移及温度和应变敏感系数可以方便解调出温度或应变，而温度和应变敏感系数的标定并非难事，也就是说，光纤沿线温度和应变感知的关键问题是布里渊频移的提取。

2 光纤沿线温度和应变快速感知方法

2.1 抛物线拟合方法存在的问题

若扫频范围围绕着布里渊频移且较小，则布里渊谱近似满足抛物线，即布里渊增益与频率的关系可近似为

式中，a、b和c均为多项式拟合系数。

针对一脉宽为100 ns、扫频范围为10.62～10.82 GHz和叠加平均次数为216的入射光，采用某商业化布里渊光时域反射仪(Brillouin optical time-domain reflectometry, BOTDR)测得布里渊谱及对应采用伪Voigt模型和抛物线的拟合结果如图1所示。由图可知，当扫频范围较小且围绕布里渊频移分布时，伪Voigt模型和抛物线都能较好地逼近实测布里渊谱。这为基于这两个函数的拟合方法准确提取布里渊频移奠定了基础。

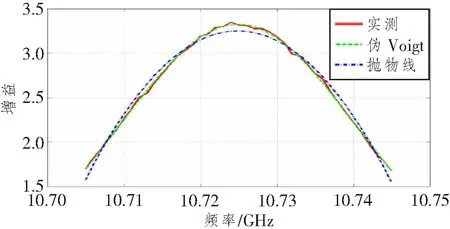
图1 实测布里渊谱及伪Voigt模型和抛物线的拟合结果

设某光纤长度为1 km，采样分辨率为1 m，布里渊谱信噪比(Signal to Noise Ratio，SNR)为10 dB和无穷大(不含噪声)，线宽为50 MHz，光纤沿线的布里渊频移为

式中:vB1的单位为GHz；z为光纤位置，单位为km。

扫频范围为10.65～10.75 GHz，扫频间隔为1 MHz，典型光纤位置下的布里渊谱如图2所示。

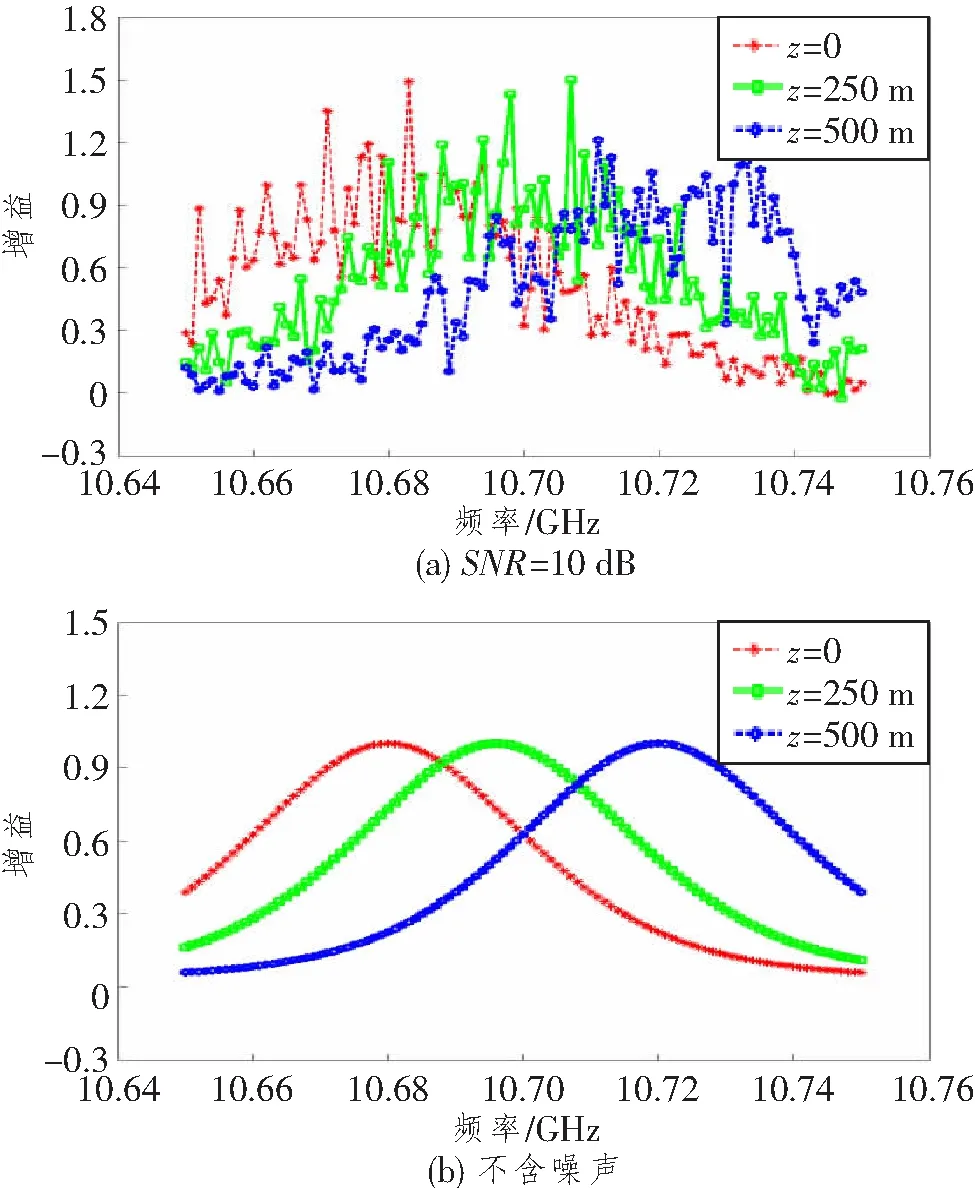
图2 典型光纤位置下,含噪声和不含噪声的布里渊谱

采用基于伪Voigt模型和抛物线的拟合方法算得光纤沿线的布里渊频移误差如图3所示。由图可知，不管布里渊谱是否含噪声，基于伪Voigt模型的拟合方法提取得到布里渊频移的误差与光纤位置基本无关。而基于抛物线拟合方法的误差显然与光纤位置有关，而且即使不含噪声，后者仍然存在明显误差。显然，以上案例中扫频范围并不是都围绕布里渊频移对称分布，下面分析是否是该因素导致基于抛物线的拟合方法产生误差。定义扫频范围偏差因子D为布里渊频移减去扫频范围中心频率。为了方便观察，图3中一并标出了扫频范围D与光纤位置的关系。

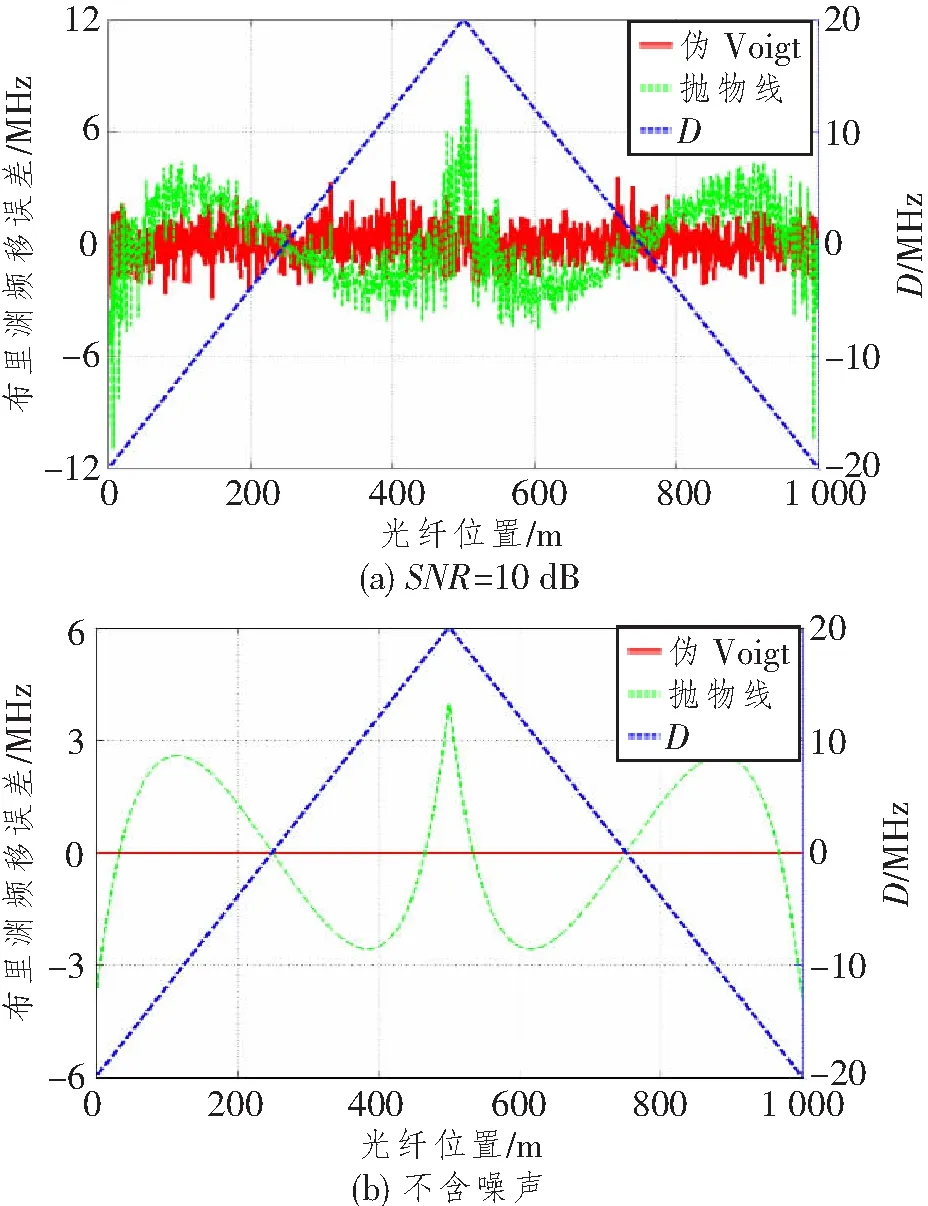
图3 不同算法算得光纤沿线的布里渊频移误差

由图3可知，当偏差因子D为0时，基于抛物线拟合方法的误差最小，对于不含噪声的情况，此时误差为0。随着D幅值的增加，基于抛物线拟合方法的误差增大。即误差随扫频范围对称程度变化成规律性变化。所以，基于抛物线拟合方法的误差受扫频范围对称程度影响很大，为了提高其准确性，需要截取围绕布里渊频移左右对称的布里渊谱用于抛物线拟合。

SNR=10 dB时，布里渊谱两种算法的平均计算耗时分别为44.97和0.47 ms，不含噪声时，两种算法的平均计算耗时分别为28.32和0.40 ms。也就是说,基于抛物线拟合方法的计算时间仅为基于伪Voigt模型拟合方法的1/97～1/70。

2.2 改进抛物线拟合方法的提出

由2.1节分析可知，扫频范围不对称会导致基于抛物线拟合方法算得的光纤沿线的布里渊频移产生误差。因此，为了提高该方法的准确性，可以从布里渊谱中选择一段围绕布里渊频移对称的部分，然后采用基于抛物线的拟合方法计算布里渊频移，这样可以提高布里渊频移提取的准确性。

对含噪布里渊谱去噪后可以更加准确地确定布里渊频移，截取的布里渊谱也具有更好的对称性。因此，考虑采用去噪算法滤波布里渊谱的噪声。在常见的去噪方法中，Savitzky-Golay滤波器采用低阶数的多项式拟合对分段范围内的信号进行滤波。由于是分段滤波，该滤波器在滤除噪声的同时，可以确保信号的整体形状和宽度不变，比较适合于对含噪布里渊谱的去噪。针对2.1节的含噪布里渊谱，采用Savitzky-Golay滤波器(多项式阶数和滤波窗长分别为4和85)滤波前后的布里渊谱如图4所示，采用滤波前后布里渊谱直接定位布里渊频移的误差如图5所示。

图4 Savitzky-Golay滤波前后的布里渊谱

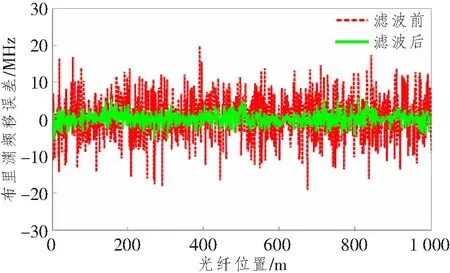
图5 Savitzky-Golay滤波前后的布里渊频移直接定位误差

布里渊频移定位的准确性会影响截取的布里渊谱的对称程度，进而影响后续基于抛物线的拟合方法对布里渊频移提取的准确性。下面分析Savitzky-Golay滤波器可调参数对布里渊频移定位准确性的影响，该滤波器可调参数为多项式阶数和滤波窗长，且要求多项式阶数要小于滤波窗长，滤波窗长必须为奇数。光纤沿线的布里渊谱仍采用2.1节方式产生，不同的是,SNR分别为10、20和30 dB。多项式阶数和滤波窗长分别在1～11和3～101(0.06ΔvB～2.02ΔvB)范围内变化，得到不同SNR时去噪后布里渊频移直接定位误差如图6所示。为了观察方便，也将不同SNR时最佳多项式阶数和滤波窗长及对应的布里渊频移定位误差以红色标于图中。

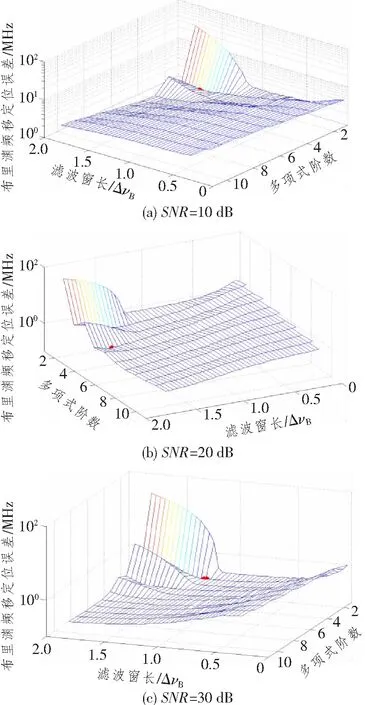
图6 多项式阶数和滤波窗长对去噪后布里渊频移直接定位误差的影响

由图可知，多项式阶数和滤波窗长对布里渊频移直接定位误差有显著影响，二者选择极大值和极小值都不利于提高布里渊频移直接定位的准确性。不同SNR下最佳的多项式阶数和滤波窗长如表1所示。

表1 不同SNR下最佳的多项式阶数和滤波窗长

由表可知，不同SNR下最佳多项式阶数和滤波窗长有一些差别。为了增加实用性，应该考虑不同SNR下选择一个固定的多项式阶数和滤波窗长。

所有SNR下的平均布里渊频移误差与多项式阶数和滤波窗长的关系如图7所示。由图可知，扫频范围为10.65～10.75 GHz、扫频间隔为1 MHz、线宽为50 MHz和布里渊频移在10.68～10.72 GHz范围内变化且综合考虑不同SNR情况下，最佳(选定)多项式阶数和滤波窗长分别为4和1.7ΔvB。为了综合观察选定参数的效果，表2给出了以上参数下的误差和不同SNR下按照表1参数的对应误差，即为最小误差。由表可知，不同SNR下选定参数对应的布里渊频移误差近似等于最小误差，这表明了选定多项式阶数和滤波窗长的有效性。

图7 多项式阶数和滤波窗长对不同SNR下平均布里渊频移直接定位误差的影响

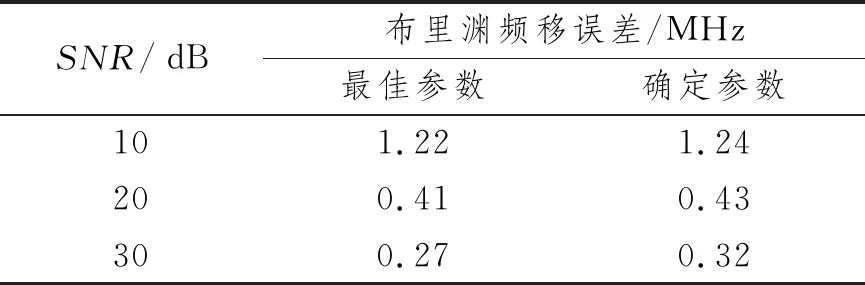
表2 选定多项式阶数及滤波窗长与最佳多项式阶数及滤波窗长对应的布里渊频移误差

3 提出方法的验证

针对2.2节的含噪布里渊谱信号，采用原始基于抛物线的拟合方法、基于伪Voigt模型的拟合方法和本文所提结合Savitzky-Golay滤波的改进抛物线拟合方法，在不同SNR下不同算法算得的光纤沿线的布里渊频移如图8所示，布里渊频移误差的统计结果如表3所示，不同算法的计算时间如表4所示。表中，EM和Estd分别为布里渊频移误差的最大值和标准差。

表3 不同算法在不同SNR下的布里渊频移误差统计值

表4 不同算法在不同SNR下的平均计算耗时

由图8和表3可知，基于改进抛物线拟合方法的布里渊频移提取准确性要远高于原始抛物线拟合方法，而与基于伪Voigt模型的拟合方法相似。由表4可知，结合Savitzky-Golay滤波的改进抛物线拟合方法的计算时间要大于原始抛物线拟合方法而远小于基于伪Voigt模型的拟合方法，前者仅为后者的1/37～1/28。

考虑到基于布里渊频移的温度和应变敏感系数典型值分别为1.12 MHz/°C和0.048 2 MHz/με，如果将光纤沿线的布里渊频移变化完全归结于温度或应变的变化，则基于以上3种算法对应光纤沿线温度或应变的测量误差分别如图9和10所示。温度和应变测量误差的统计结果分别如表5和6所示。与布里渊频移提取情况类似，采用改进抛物线拟合方法时，温度和应变测量准确性远高于原始抛物线拟合方法，而与基于伪Voigt模型的拟合方法相近。显然，本文提出方法从解调角度为基于布里渊散射的分布式光纤传感中温度和应变的快速感知奠定了基础。

图9 不同算法在不同SNR下的光纤沿线温度误差

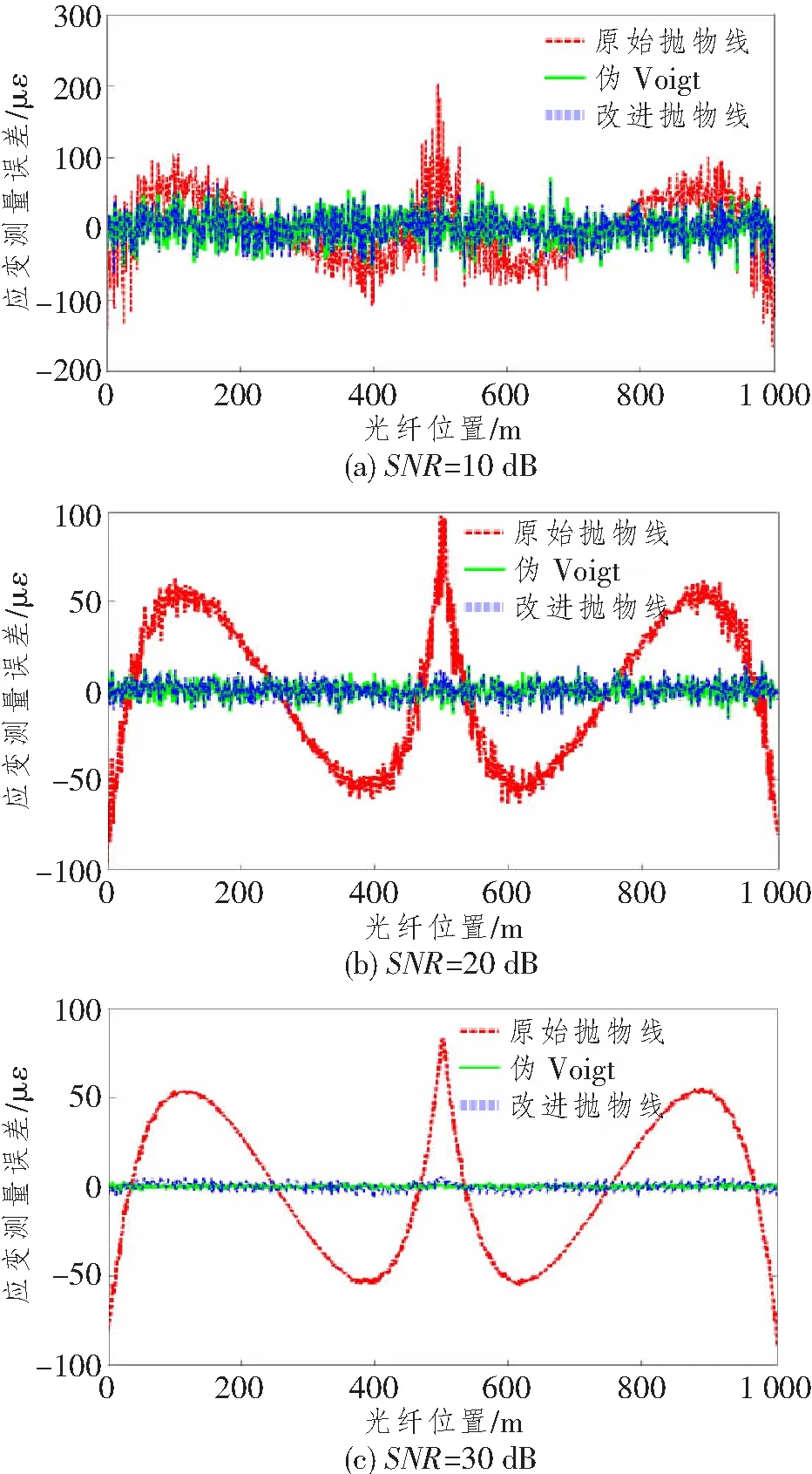
图10 不同算法在不同SNR下的光纤沿线应变误差

表5 不同算法在不同SNR下的温度测量误差统计值

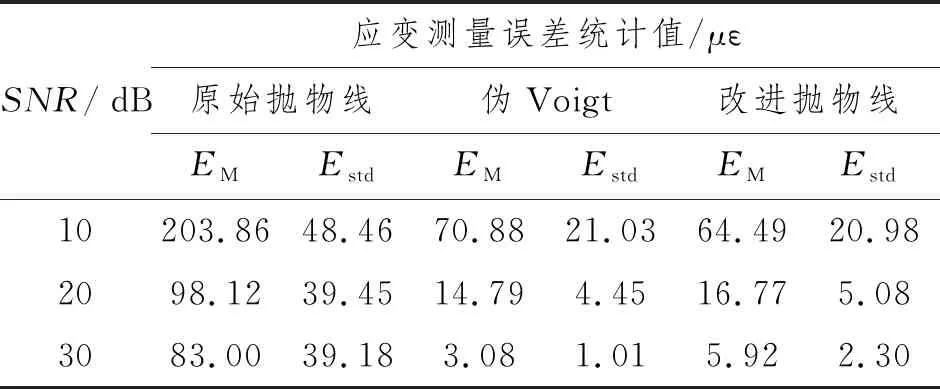
表6 不同算法在不同SNR下的

4 结束语

考虑到基于抛物线的拟合方法在扫频范围存在偏差时提取得到的布里渊频移存在误差，为了提高布里渊频移提取的准确性，同时使计算时间不会显著增加，本文提出了一种结合Savitzky-Golay滤波的改进抛物线拟合方法。采用光纤沿线的温度或应变波动的布里渊谱进行了验证，验证结果表明，本文所提方法具有与经典的基于伪Voigt模型拟合方法类似的准确性，同时计算时间仅为基于伪Voigt模型的拟合方法的1/37～1/28。