有关平衡态近似的一个问题

史济斌 刘国杰

(华东理工大学化学系 上海 200237)

在反应机理的拟定中，平衡态近似是一种重要方法。这种方法的特征是，中间物转变成产物的速率很慢，以致它有足够的时间逆转成反应物，并与反应物建立近似的化学平衡关系。由于中间物转变成产物的速率很慢，这一步便成了速率控制步骤，复合反应的反应速率就近似地等于这一步的反应速率。因此，人们只需求得速控步的反应速率就能方便地得到复合反应的反应速率。但是，这种简便有时也会因疏忽大意而导致错误的结果，下面以臭氧分解反应为例来予以说明：

(1)

据此，Chapman[1-2]和Benson[3]提议该反应的机理为：

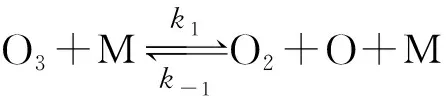
在充足的氧气氛下，可以认为k-1c(O2)c(O)cM≫k2c(O)c(O3)，故适合平衡态近似。其中第②步为速控步，该步的反应速率可看作复合反应的反应速率。因此，有：

(2)

式中中间物O的浓度可由第①步化学平衡关系得到:

(3)

将式(3)代入式(2)，得：

(4)

式中k=k1k2/k-1。式(4)与实验建立的动力学方程(式(1))似乎很一致。

但是，仔细审查不难发现，式(4)并不可靠。因为氧原子是个活泼的中间物，它一经生成便会很快消耗，在系统中的浓度很小，因此，上述机理也可用稳定态近似处理。

按照稳定态近似：

(5)

(6)

因此，臭氧的消耗速率应为:

(7)

式(7)中代入了式(6)。由于反应是在充足的氧气氛下进行，故k-1c(O2)cM≫k2c(O3)，式(7)可简化为：

(8)

式中的k=2k1k2/k-1。由此可见，式(8)是式(4)的2倍。

倘若用产物O2的生成速率表示反应速率，得到的结果也是类似的，只是速控步的反应速率应为：

(9)

代入式(3)可得O2的生成速率为:

(10)

但式(10)也不可靠。因为按照稳定态近似，O2的生成速率应为：

k1c(O3)cM+(2k2c(O3)-k-1c(O2)cM)c(O)

(11)

将式(6)代入式(11)，则得：

(12)

考虑到在充足的氧气氛下，k-1c(O2)cM≫k2c(O3)，可见，式(12)是式(10)的1.5倍。

那么，问题出在哪里呢？为什么两种近似处理的结果会有如此明显的差异呢？

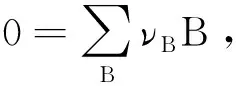
反应速率的定义为：

(13)

式中νB为化学计量数，对于反应物νB取负号，对于产物νB取正号。因此，式(13)可表示为：

(14)

如果B为反应物A，则定义:

(15)

称υA为反应物的消耗速率。

如果B为产物P，则定义:

(16)

称υp为产物的生成速率。

3种速率间的关系可由式(14)看出：

υA=|νA|υ或kA=|νA|k

(17)

υP=νPυ或kP=νPk

(18)

式中k、kA和kP分别为化学反应的反应速率系数、反应物的消耗速率系数和产物的生成速率系数。

由此可见，反应物的消耗速率系数和产物的生成速率系数分别与它们的化学计量数的绝对值成正比。也就是说，同一个反应物(或产物)的消耗(或生成)速率系数对于复合反应和机理中不同的基元反应其值是不一定相同的。上述问题就出于此。

按照平衡态近似，复合反应的反应速率近似等于速控步的反应速率。这个关系可由下式表示：

υ复合≈υ速控步

(19)

(20)

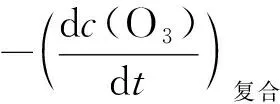
(21)

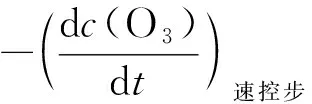
将式(20)和式(21)代入式(19)，则得:

(22)

这就是说，复合反应的臭氧消耗速率应是速控步臭氧消耗速率的2倍。因此，式(2)右端必须乘上2才是复合反应的臭氧消耗速率，也即式(4)中的k应为：

(23)

这便与稳定态近似所得的结果式(8)完全一致。

倘若反应速率以产物O2表示，则速控步的反应速率应表示为：

(24)

(25)

将式(24)和式(25)代入式(19)，便知复合反应中O2的生成速率是速控步O2的生成速率的1.5倍，即：

(26)

将式(10)代入式(26)，所得结果便与式(12)相同，两种近似便不再矛盾。

利用平衡态近似，也会遇到与臭氧分解反应类似的问题，这里不再展开。

综上所述，本文的结论是：在用平衡态近似拟定反应机理时，需要注意这样一个问题：虽然速控步的反应速率可视为复合反应的反应速率，但是这两个反应中同一反应物(或产物)的消耗速率(或生成速率)却不一定相等，因为消耗速率和生成速率分别与反应物和产物的化学计量数的绝对值成正比。对于本文所述的臭氧分解反应，不管是反应物O3，还是产物O2，它们在复合反应和速控步中的化学计量数都各不相同，因此，两个反应的O3的消耗速率或O2的生成速率是不相等的。由于实验测得的式(1)是复合反应的臭氧消耗速率方程，而式(2)和式(4)得到的是速控步中O3的消耗速率，故必须将式(4)代入式(22)，才能获得复合反应中O3的消耗速率方程。

参 考 文 献

[1] Chapman D L,Clarke H E.JChemSoc,1908,93:1638

[2] Chapman D L,Jones H E.JChemSoc,1910,97:2463

[3] Benson S W,Axworthy A E.JChemPhys,1957,26:1718

[4] Moore J W,Pearson R G.Kinetics and Mechanism.3rd ed.New York:John Wiley & Sons,1981