黑龙江省农业发展绩效与影响因素分析

郭 锦，陈 昭

（广东外语外贸大学a.公开学院；b.国际经贸学院，广州 510420）

1 导言

农业发展是国民经济的根本和基础。从全球来看，粮食安全一直是很严峻的问题。中国是发展中的农业大国，耕地面积仅占世界的7%，而人口却占世界的22%，十几亿人的粮食问题始终是头等大事。由于人口增长和人民生活水平的提高，今后每年粮食需求将以50亿公斤左右的刚性速度增长。另一方面，工业化和城市化使得耕地面积不断减少，到2020年即使能够守住18亿亩的红线，也只能够达到人均1.2亩。因此，高度重视、保护和提高粮食综合生产能力，建立稳定的商品粮生产基地，建立符合我国国情和社会主义市场经济要求的粮食安全体系，确保粮食供求基本平衡，这既是我国政府解决粮食安全问题的基本方针，也是实现粮食安全总的目标。

黑龙江省是我国的农业大省，地理优势和自然资源得天独厚，耕地面积占全国总量的十分之一。2009年，黑龙江省粮食产量达870.6亿斤，连续6年夺取丰收，粮食总产居河南省之后列中国第二位。充分发挥黑龙江省在我国农业发展中的重要作用，对于保障我国的粮食安全意义十分重大。

1 模型的建立

我们选取黑龙江省的哈尔滨、齐齐哈尔、鸡西、鹤岗、双鸭山、大庆、伊春、佳木斯、七台河、牡丹江、黑河、绥化、大兴安岭作为面板模型的截面研究对象，原因是在我们选取的样本区间内，上述地区的GDP和农业生产总值分别占黑龙江省GDP和农业生产总值的比重范围在94%-99%，可见上述地区的农业发展能够代表黑龙江省农业发展问题。

变量名称和符号界定如下：Yit表示粮食产量 （单位：万吨），Lit表示农村劳动力投入（单位：万人），Hit表示农业化肥投入量（单位：吨），Nit表示农机总动力（单位：万千瓦），Mit表示耕地面积（单位：万公顷）。其中i表示截面个体，指上文的各个地区；t表示时间序列，文中为1995～2009年。

假设农业产出函数是柯布——道格拉斯型的，因此可以建立对数函数模型如下：

其中，ln 表示对变量取对数，Ci为非观测效应，b0、b1、b2、b3为待估参数，u为特异误差。

2 基于面板单位根和面板协整检验的实证分析

2.1 数据的来源和说明

本文所用数据样本区间为1995～2009年，这是因为这一时间段黑龙江农业发展稳定，因此确定研究样本区间为上述时间段。所有数据均来自于有关年度《黑龙江统计年鉴》等权威数据资料库。本文所用软件是Eviews5.1和Stata9.0。

2.2 面板模型与估计、检验方法

计量经济理论表明，众多经济变量尤其是面板数据大都是非平稳变量，用非平稳变量进行回归分析结果很大程度上表现为伪回归。为避免伪回归现象，需要对面板数据进行单位根和协整检验。

（1）面板单位根检验。面板模型进行回归分析之前进行单位根检验，这是避免出现伪回归的前提条件。面板单位根检验方法有别于时间序列数据单位根检验，主要为：LLC检验、Breitung检验、Hadri检验是相同根的检验方法，IPS检验、Fisher-ADF检验是不同根的检验方法；LLC检验、Breitung检验、IPS检验、Fisher-ADF检验原假设是含有单位根；Hadri检验原假设为不含有单位根。本文所用数据和变量的面板单位根检验结果如表1所示。

上述检验结果除了lnY、lnH、lnM一阶差分值的Breitung检验显著与众不同外，其他四种或以上检验方法检验结论一致，均表明上述变量是I(1)的，也就是说本文模型所用变量是非平稳变量。

表1 面板数据的单位根检验

对于面板模型，如果变量是非平稳的，进行回归分析之前需要进行协整检验，以判断是否可能属于伪回归。

（2）面板协整检验。Pedroni(1999，2001)以回归残差为基础构造出7个统计量进行面板协整检验，其中除了Panelνstat为右尾检验之外，其余统计检验量均为左尾检验。4个是用 联 合 组 内 尺 度 描 述 即 Panel v-Stat、Panel ρ-Stat、Panel ADF-Stat、Panel PP-Stat；另外3个是用组间尺度来描述即Group ρ-Stat、 Group ADF-Stat、 Group PP-Stat。 如果各统计量均在1%(或5%)的显著性水平下拒绝“不存在协整关系”的原假设，表明非平稳的时间序列之间存在着协整关系。

Pedroni(1999，2001)基于残差的协整检验量最关键的是计算所假设协整方程的残差。

对于如下的协整方程：

其中，β1=（β1i，β2i，…，βMi），xit=(x1i,t,x2i,t，…，xMi,t)，M 为独立变量的个数。

为了得到相关的面板协整统计量，首先要估计协整方程。为了得到两个组内统计量 （panel rho-stat、panel t-stat）值，对原序列进行差分运算并估计如下差分方程：

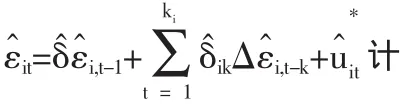
Pedroni对于相关的面板协整检验量作了如下的表示：

对于每个面板模型利用近似的均值和方差既可以进行标准化。

对于面板协整检验而言其原假设H0：对∀i,γi=1，即不存在协整关系；而对于组间统计量而言其备择假设为：H1：对∀i，γi＜1：而对于组内统计量而言其备择假设为：H1：对∀i,γi=γ＜1。

本文所用变量的面板协整检验结果如表2所示。

表2 本文所用变量的面板协整检验

模型变量的Pedroni协整检验的组内和组间统计量在1%的显著水平上均表明拒绝不存在协整关系的原假设，表明前文模型存在协整关系，可以直接进行回归分析，不存在伪回归。

（3）实证结果。按照协整检验的结果，我们对模型进行了回归分析，模型检验表明应该采用随机效应模型，方法为SUR（似不相关回归），回归结果如下。

Ci的结果如表3所示（由于取了对数，因此结果出现负数，数越小表明农业自主产量越小，反之则反是）。

回归方程的系数表明的是弹性，按照数值大小顺序排列，解释变量对于农业增长的贡献分别是农机总动力、化肥施用量、农作物耕作面积和农业劳动力投入。如果把农业劳动力投入对于农业产出的贡献度设定为1，则农作物耕作面积对于农业产出的贡献度为1.32，化肥施用量的贡献度为2，农机总动力的贡献度为5.6。

表3 各地区农业自主产量的对数值 单位：万吨

按照回归模型计算各地区解释变量的系数，即弹性，结果如表4所示。

从劳动力投入弹性来看，齐齐哈尔和鹤岗为正数，其他地区不显著或者为负数；而化肥施用量弹性除了鹤岗、大兴安岭为负数以外，其余地区均为正数，以双鸭山、牡丹江弹性为最大；哈尔滨、伊春、七台河、黑河、大兴安岭的农机总动力弹性系数为正数，绥化的弹性系数不显著，其余地区系数均为负；齐齐哈尔、鸡西、鹤岗、绥化、大兴安岭的农作物耕作面积弹性大于0，其他地区或者不显著或者小于0。

表4 各地区解释变量的系数

3 结论和政策建议

理论和实证分析结果表明，四种投入要素与黑龙江农业产出正相关。黑龙江省农业劳动力投入和化肥施用量的增加、农机总动力的提高、农作物耕作面积的扩大显著的提高黑龙江农业产出，并且农机总动力对黑龙江农业产出贡献度最大，其次是化肥施用量和农作物耕作面积的提高，贡献最小的是农业劳动力投入。农机总动力对农业产出的贡献是居第二位贡献的化肥施用量的2.8倍。从各地区来看，各要素投入对于农业产出的贡献明显不同，差异显著。哈尔滨、七台河和黑河农业产出贡献大的投入要素是化肥施用量和农机总动力；齐齐哈尔农业产出贡献度大的要素是耕作面积、劳动力投入和化肥施用量；鸡西和绥化为耕作面积和化肥施用量；鹤岗是耕作面积和劳动力投入；双鸭山、大庆、佳木斯和牡丹江则是化肥施用量；伊春是农机总动力和化肥施用量；大兴安岭是农机总动力和耕作面积。

上述分析结果表明，要素投入的增加能够促进黑龙江农业产出的提高，农业总产出弹性约为1.1（0.11+0.22+0.62+0.145），表现为规模报酬递增，也就是从理论上说，各种要素投入平均增加1%，黑龙江农业产出将增加1.1%。但是从不同地区来看，由于各地区的要素弹性不同，采用不同的要素投入组合能够有效提高农业产出水平，并且能够使资源得到合理有效的利用。比如，哈尔滨的耕地面积2719万亩，人均耕地2.76亩，是全国人均耕地的2倍，土地粗放型耕种面积大；黑河地区耕地总面积为1883万亩，85%的耕地种植大豆；这两个地区粮食播种面积占农作物总播种面积的比重超过了90%，农业基本情况更适合集约化经营，增加农机投入和化肥施用量，会更有效提高该地区农业产出，这和理论模型的分析是一致的。

粮食播种面积增量占黑龙江省增量比重较大的有绥化（14.8%）、齐齐哈尔（14.7%）。齐齐哈尔和绥化两个地区耕作面积弹性对于农业产出的贡献度最大，适合扩大面积提高农业产出类型的农业发展模式；其他地区耕作面积对于农业产出弹性则很小、不显著或者负相关，因此这些地区农业发展实事和理论分析一致。农机总动力弹性以大兴安岭最高，为3.337。由此可见黑龙江各地区农业发展是很有绩效的，合理的资源分配和恰当的要素组合促进农业得到较好的发展。

我们总的结论和建议是，由于各地区自然条件和资源禀赋不同，不同地区的农业发展应该采用不同的措施和办法，要因地制宜，通过要素投入组合的合理配置，才能有效提高农业产量。否则，无效的配置是对资源的浪费。不同问题采取不同的处理方法，而不应该搞一刀切，发挥地区的优势，回避劣势，扬长避短，则能促进经济和社会整体绩效的提高。

[1]乔榛，李白.结构、制度与观念：黑龙江省农村经济发展的瓶颈[J].学术交流,2006，(8).

[2]刘玉铭，刘伟.土地制度、科技进步与农业增长——以1952—2005年黑龙江垦区农业生产为例[J].经济科学，2007，（2）.

[3]Levin,A.,C.Lin，C.Chu.Unit Root Tests in Panel Data:Asymptotic and Finite-Sample Properties[J].Journal of Econometrics,2002,108.

[4]Im,Kzing So，M.Hashem Pesaran，Yong cheo Shin.Testing for U-nit Roots in Heterogeneous Panels[J].Journal of Econometrics,2003,115.

[5]Pedroni P.Panel Cointegration Asymptotic and Finite Sample Properties of Pooled Time Series Tests，With an Application to the PPP Hypothesis[C].Revised Working paper,Indiana University.2001.

[6]Pedroni P.Panel Cointegration Asymptotic and Finite Sample Properties of Pooled Time Series Tests,With an Application to the PPP Hypothesis[C].New Results.Working Paper,IndianaUniversity,1997.