风险价值法VaR对套利风险的衡量研究

景 楠

（西安外国语大学 商学院，西安 710000）

在期货套利交易中，投资者最关心的问题，莫过于建仓之后到平仓退出之前这段持有期内如何规避风险。由于投资者存在大量未结清的头寸，在持有期内其头寸价值的变化将导致收益的变化，同时也直接影响到所占用保证金的变化。

为了从数量上衡量和控制套利交易的风险，我们试图引入西方现代风险管理方法VaR，对投资者对手中所持有的套利交易资产组合的风险价值在一段时间内或者每天进行估值和计量，将计算出的风险大小与自身对风险的承受能力加以比较，以此来决定投资额和投资策略，及时调整套利资产组合，减少投资的盲目性，从而达到分散和规避投资风险，尽可能地减少因投资决策失误所带来的损失。

1 VaR计算的方法选择

本文主要以金属期货跨市套利投资组合的风险进行定性和一定的定量研究，为投资者的投资提供量化的决策依据。

VaR的计算方法可以分为三种：

(1)方差协方差法。这是最简单的方法，它假设资产收益率是风险因素的线性（或德尔塔）函数，并认为风险因素是正态的，并运用期望值和方差获得VaR结果。但是，一旦某资产的回报率是非正态分布的，其计算的结果就会出现偏差。

(2)历史模拟法。历史模拟法提供了一种简单直观、易于解释的完全估值方法，根据实际价格估计，这个方法允许非线性和非正态分布，不需要确切知道合约价格、收益的分布函数。其完全估值是通过历史数据来实现的，它不需要对定价模型和市场的随机结构做出某种特定的假设。它也考虑了“厚尾”问题，而且不依赖于特定的定价模型，因此，历史模拟法一般不会出现模型风险。

(3)蒙特卡洛模拟法。相对而言，这一方法在概念上和计算上比较复杂，对电脑资源的要求也很高,因此在应用上没有前两种方法广泛。当投资组合较为庞大时，很可能会由于硬件限制而无法完成计算。这种方法建立在投资组合收益可供允许简单模拟的基础之上，生成基于既定概率分布之上的随机结果，从而获得VaR的值。

在对上述方法作出权衡的基础上，我们选取历史模拟法来计算VaR。

在计算期货头寸VaR的过程中，要确定一个套利资产组合的VaR值必须首先要确定以下两个参数：一是持有期间的长短；二是置信度的大小。实际上还有第三个，就是观测期间。因为从不同的期间观察，VaR的值是不一样的。

持有期间是一项基本因素，在其余方面相同的情况下，10天的VaR比1天的VaR要大。对于持有期间的选择与金融机构或投资机构的业务种类和所分析的资产组合有关。头寸的持有期限究竟选择1天、2天，亦或更长的时间，同测量者的偏好相关。对于流动性比较大的资产组合，最好选择1天的时间段。比如对于需要按季度调整组合并报告业绩的投资银行业务来说，90天是比较合适的。理想的情况是，持有期与投资组合定期清算所需的最长时间相一致为宜。

置信度越大，VaR就越大，一旦发生损失，则损失的额度就越大；置信度越小，VaR就越小，一旦发生损失，则损失的额度就相对较小，但也存在可能低估在极端情况下出现的损失。5%或1%的概率是否可以被视为“小概率事件”或“极端情形”呢，从风险控制的角度来看，这只是个选择的问题（JP摩根银行在计算VaR时使用的是95%的置信水平）。置信度的选择与风险管理者处理小概率事件的能力以及期货经纪公司对客户爆仓损失的容忍程度有关。风险管理者的应变能力比较强，期货公司对损失的容忍度比较大，就可以选择比较高的置信度，也就是选择比较低的保证金水平。比较低的保证金能给期货公司带来竞争力，从而有利于提高佣金收入。对于个人投资者而言，也可以通过由期货公司或投资机构提供的不同置信度区间下的VaR值，来判定手中所持有的投资组合是需要继续持有还是平仓止损。

作为一个统计数值，VaR的值是随着时间的推移而变化的。在上述两个参数不变的情况下，如果市场波动趋于活跃，那么VaR的值应当变大；如果市场波动趋于平缓，那么VaR的值应当缩小。这就要求我们在使用VaR方法的时候要及时重新计算VaR值，观察期间当然要包括最新的市场数据，并适当回溯历史。在选择观察期间长度的时候，既要考虑保持VaR值的稳定性，又要使其能更多的反映市场最新的变化。

目前国内在期货领域应用VaR方法主要局限于计算合约单边头寸的VaR（比如石油期货等）方面，涉及期货合约投资组合VaR的相关论文则并不多见。本文主要从套利投资组合的角度来研究期货合约的VaR，通过套利投资组合的VaR与单边头寸VaR的比较，可以使投资者对于哪一种是较低风险的投资策略一目了然。由于套利组合的VaR值能够把对预期的未来损失的大小和该损失发生的可能性结合起来，所以它不仅可以使投资者能够明白发生损失的规模，而且知道损失发生的可能性。

2 套利投资组合以及单边头寸的VaR（平均）衡量公式

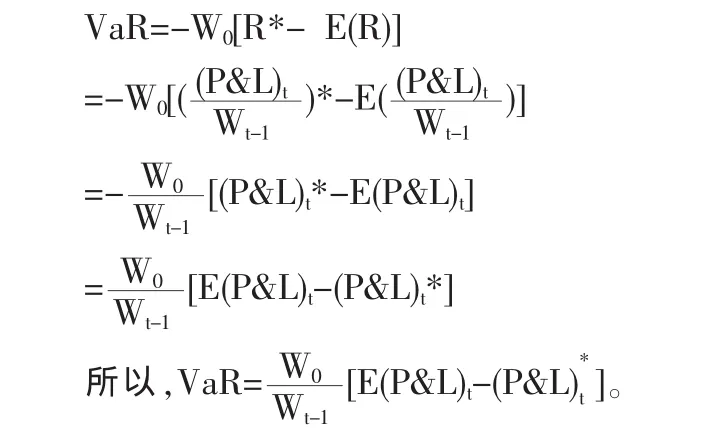
据上式，套利投资组合的风险价值为：

风险价值有绝对风险价值和相对风险价值。本文主要探讨相对风险价值。对于一般分布的资产而言，相对风险价值的计算公式为 VaR[5]（平均）=E(W)-W*，其中，W＝W0（1+R）表示资产的价值，W*=W0（1+R*）表示在给定置信水平下资产的最小价值，W0为初始投资额，R为资产的收益率。

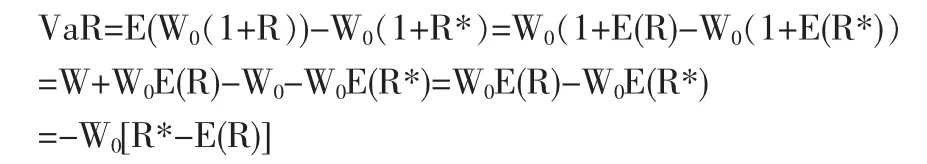
对于期货合约而言，最容易获得的数据是合约的浮动盈亏即收益而不是合约的收益率。浮动盈亏包括浮动盈利和浮动亏损，浮动盈亏能够反映期货头寸的价值变化。浮动盈利越小(浮动盈亏越大)，期货头寸的价值就越低；头寸最小价值正好同头寸的最大浮亏相对应。事实上，在计算VaR的过程中，引入浮动盈亏或者头寸收益较收益率更为直观，能够大大缩小计算量，有效降低运算成本，但数据的精确性并不会受到影响。

持有期为1天的期货合约投资收益率可以定义为当日合约的浮动盈亏同前一天的合约价值之比或当日合约的浮动盈亏同当天的保证金之比。本文采用前者进行定义，所以，期货头寸的收益率为投资组合价值建立的伦铜单边头寸风险价值为：

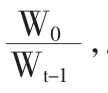
投资组合价值建立的沪铜单边头寸风险价值为：所以决定风险价值比较结果的因素为方程左边的第二个因子，那么，风险价值可以作如下变化：

套利投资组合的风险价值记为：

投资组合价值建立的伦铜单边头寸风险价值记为：

投资组合价值建立的沪铜单边头寸风险价值为：

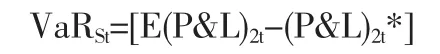
如果去掉时间下标，上述三公式为：

根据上述公式计算出的结果将是持有期为1天的VaR。如果持有期为2天、3天、30天或者更长的时间，那么就需要重新计算，因此，对于投资者而言，风险价值必须每天作一次新的记录并长期观察，才能在一段指定的持有期或观测期内比较风险价值VaR是否出现较大的变化。

3 实例分析

我们主要以金属期货市场上最常被投资机构和投资者采用的期铜正向跨市套利交易投资组合、伦铜多头、沪铜空头为例，具体说明如何计算基于头寸价值的单边头寸VaR的原理和步骤（这里伦铜系指伦敦金属交易所铜标准期货合约，沪铜系指上海期货交易所标准铜期货合约）。

跨市套利是指在某个交易所买入或卖出某一交割月份的某种商品期货合约的同时，在另一个交易所卖出或买入同一交割月份的同种同样标的数量的商品合约，以期将来在某个有利时机的在两个交易所分别对冲持有的合约来获利。我国的铜期货套利一般是指在伦敦金属交易所(LME)买入或卖出某一交割月份的铜期货合约的同时，在上海期货交易所(SHEF)卖出或买入同一交割月份的相同吨数的铜期货合约，以期将来对冲获利。铜期货套利有正向套利和反向套利两种。正向套利是指在伦敦金属交易所买进期铜合约的同时，在上海期货交易所卖出期铜合约，将来于某个有利时机分别对冲获利。反向套利则正好与之相反。

从理论上讲，VaR的计算根据不同置信度 （如95%，95.5%，96%，99%等等）的个数C，不同的观测值数量 （如500，1000，1500等等）的分类N和不同的持有期（如1天，2天，30天，60天等等）的个数H进行计算，共有N*C*H种不同的VaR。考虑到计算成本和典型性，笔者计算几种有代表性的VAR来说明投资组合以及各头寸的风险VaR比较。置信度水平选择95%和99%（即显著性水平为5%和1%），持有期限为1天，观测数据的样本量为1500个。

由于两类资产之间是负相关的，多空组合能够更大程度的降低投资组合风险。为了计算上的方便，虚拟一个的基本的套利投资组合，组合的总金额设定为购买一手沪铜空头合约价格与购买一手伦铜多头合约价格 （根据即期汇率折算为人民币）之和。相应的可以求出伦铜和沪铜合约各自所占的权重。同时，投资组合总金额的变动会导致VaR成比例的变动。

由于利率、关税率、增值税率、P(t)基本上在一个较长的时期内是相当稳定的，所以我们忽略了这几项因素以简化VaR模型。

我们选取1500个观测值,置信度设为99%，持有期为1天，计算基于浮动盈亏的伦铜多头和沪铜空头构成的套利投资组合（正向套利投资组合）、伦铜多头、沪铜空头的VaR。

(1)构造基本的伦铜多头和沪铜空头套利投资组合

伦铜期货合约为每手25吨，而沪铜期货合约为每手5吨，所以，构造一个基本的伦铜和沪铜套利投资组合需要1手伦铜期货合约和5手沪铜期货合约，即25吨伦敦期铜和25吨沪铜期货合约。正向套利基本投资组合是在LME买进1手伦铜期货合约的同时，在SHEF卖出5手沪铜期货合约。

根据数据，我们可以构造期铜跨市正向套利投资组合，虚拟套利投资组合由两个对冲头寸构造而成，以伦铜折算为人民币的价格建立1单伦铜多头合约（为了计算上的简化全部取整数），标的数量为25吨，同时以上海沪铜的价格建立5单沪铜空头头寸，标的数量亦为25吨。

(2)分别计算伦铜多头和沪铜空头在投资组合中所占的权重

根据马科维茨的均值-方差模型，正向套利投资组合的价值公式一般形式

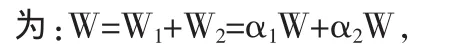
其中，α1＝W1/W，α2＝W2/W，W 表示套利投资组合的价值，W1表示伦铜多头价值，W2表示沪铜空头价值，α1表示伦铜多头在投资组合中所占的权重，α2表示沪铜空头在投资组合中所占的权重。

其中，q1，q2分别为伦铜和沪铜的标的数量，单位为吨；p1，p2分别为伦铜和沪铜期货每吨报价，伦铜的报价是采用汇率调整后的人民币价格。

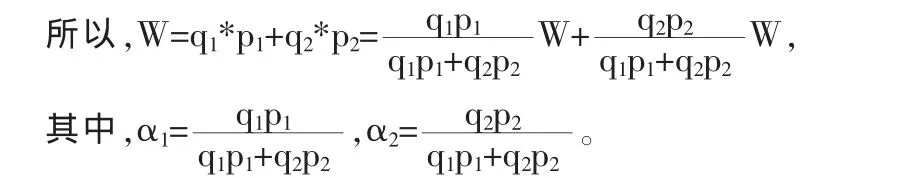
当投资组合的头寸数量确定之后，也就是q1，q2的值确定后（q1=q2=25吨），那么投资组合的权重只同各合约的价格相关。

对于上述投资套利组合，其价值为W=q1*p1+q2*p2。伦铜多头头寸的权重为α1=[p1/(p1+p2)]，沪铜空头头寸的权重为α2=[p2/(p1+p2)]。

采用上述权重公式，我们可以计算出从1996年1月3日到2009年12月31日基本套利投资组合的头寸权重。头寸权重的具体数值见图1

上述头寸权重图中，α1的均值为0.45，α2的均值为0.55，因此，在计算投资组合价值构造的单边头寸数量的过程中，α1取值0.45，α2取值0.55较为合理。

图1 跨市套利投资组合的头寸权重表

(3)计算用套利投资组合价值构建伦铜多头单边头寸或沪铜空头单边头寸的数量

用投资组合的总价值所构建的单边头寸的数量等于投资组合的价值与单边头寸单价的商。所以，伦铜多头和沪铜空头的单边头寸数量头寸的数量计算如下：

因此，伦铜多头单边头寸数量：

沪铜空头单边头寸数量：

这一计算的意义在于当求出每吨或一份合约的风险价值VaR之后，可以运用上述关系求出单边头寸的VaR。

4 结论

从以上实例分析可知，VaR主要适用于正常市场条件下对于市场风险的衡量，由于统计模型预测值的准确性在很大程度上取决于有效历史数据的充分性，因而对数据有较为严格的要求。在正常市场条件下，资金的交易数据比较丰富，使用VaR模型较为有效，而当市场远离正常状态时，资产价格的关联性被割断，流动性全部消失如爆发金融危机或发生期货市场事件时，使用VAR就无法衡量此时的市场风险。

尽管VaR存在一定的缺陷，但这并不防碍它成为衡量市场风险的一个极为有价值的统计技术方法，VaR一经产生即以其对风险衡量的科学、准确、实用和综合的特点受到包括监管部门在内的国际金融界的普遍关注，迅速发展成为风险管理的一种标准。VaR及其指标变量，几乎被每一个主要的衍生金融工具交易商和越来越多的投资者及最终用户所广泛应用。

[1]周大庆等.风险管理前沿——风险价值理论与应用[M].北京：中国人民大学出版社，2004.

[2]宋逢明.金融工程原理－无套利均衡分析[M].北京：清华大学出版社，1999.

[3]John F.Marshall，Vipul Bansal.金融工程[M].宋逢明等译.北京：清华大学出版社，2005.

[4]Cormac Butler风险值概论[M].于研等译.上海：上海财经大学出版社，2002.

[5]Cormac Butler.风险值概论[M].于研等译.上海：上海财经大学出版社，2002.