正负关联规则两级置信度阈值设置方法

陈 柳，冯 山

(四川师范大学数学与软件科学学院，成都610068)(*通信作者电子邮箱634050177@qq．com)

0 引言

关联规则挖掘(Associated Rule Mining)是重要的数据挖掘研究课题。传统关联规则挖掘只研究AB型规则［1－3］。实际上AB、AB和AB型负关联规则普遍存在，自项集负相关(Negative Relationship of Itemset)［4］提出以来，其研究得到广泛关注［5－15］。正负关联规则挖掘中，限制规则数量和提取真正有趣的规则是挖掘算法设计的关键［6］。传统算法通常采用支持度－置信度框架［1］来达到该目的。但是，当同时挖掘各型正负关联规则时，使用支持度－置信度框架理论可能会出现相互矛盾的规则［7］，如AB和AB或AB和AB同时出现。为此，人们引入了相关性度量对支持度－置信度框架进行扩充和修改以避免其发生［6－10］。在相关度－支持度－置信度框架下的正负关联规则挖掘中，围绕相关性度量和支持度阈值设置的研究已比较完善。文献［8－9］采用卡方测量项集相关性。文献［6－7，10］针对卡方无法判断项集正相关还是负相关的不足，提出采用Lift度量。文献［11］对比分析了7种相关性度量方法的内在联系与区别，给出了它们各自的适用范围。文献［12］提出了约束正负关联规则挖掘中频繁项集与非频繁项集数量的一种两级支持度阈值法。在文献［12］基础上，文献［13］提出了多级支持度阈值法以进一步限制规则数量。文献［14］将多支持度法应用到正负关联规则挖掘算法中，有效地限制了规则数量。但是，在相关度－支持度－置信度框架下，现有正负关联规则置信度阈值设置方法还存在局限。文献［8］针对单级置信度阈值法阈值设置较低会产生过多低可信度规则和设置较高又会遗漏有趣规则的不足，提出四置信度阈值法，但各个阈值的设定并未考虑不同类型规则置信度间的内在约束。为此，文献［7，10］在考虑了规则置信度间的内在变化与约束关系后，以四种关联规则同时挖掘为前提，提出对AB、AB类规则和AB、AB类规则分别设置不同置信度阈值P-mc和N-mc(P-mc+N-mc=1)的双阈值法，但该方法仍然难以有效控制低可信度规则的数量，并且易遗漏有趣规则。

本文结合规则的项集相关性和正负关联规则置信度随项集支持度取值大小变化的内在特点，提出了一种新的正负关联规则两级置信度阈值设置方法(Positive and Negative association rule's TWO Minimum Confidence，PNMC-TWO)。理论推演和实验结果均表明，新方法能更有效控制正负关联规则的数量和提取有趣关联规则。新方法充分结合了四种规则置信度的变化规律，对置信度阈值的设置不是盲目的，基于它所提取的知识或规则更可靠和有效。

1 预备知识

1．1 关联规则的支持度－置信度框架

设 I={i1，i2，…，in} 是问题域的项集，D={T1，T2，…，Tm}是事务数据库，|D|表示事务个数，Ti由事务标识符TIDi和对应的项集ITi描述，ITiI，1 ≤i≤|D|。项集 AITi时称事务Ti支持A，sup_c(A)表示项集A在D中的支持度计数，则A在D中支持度sup(A)=sup_c(A)/|D|。设ms是支持度阈值，sup(A)≥ms时称项集A为频繁项集。

定义1 关联规则支持度。D中同时包含规则前件和后件的事务在D中的占比，简记sup。

定义2 关联规则置信度。D中同时包含规则前件和后件的事务在包含前件的事务中的占比，简记conf。

支持度－置信度框架:在D中筛选出同时满足支持度阈值(ms)和置信度阈值(mc)的强关联规则。

1．2 负关联规则支持度与置信度的计算方法

sup(A)=1－sup(A)

sup(A∪B)=sup(A)－sup(A∪B)

sup(A∪B)=sup(B)－sup(A∪B)

sup(A∪B)=1－sup(A)－sup(B)+sup(A∪B)

由定义2，负关联规则的置信度计算方法如下:

1．3 正负关联规则的相关度－支持度－置信度框架

在正负关联规则挖掘中，为了避免矛盾规则的出现，可在支持度－置信度框架中加入项集相关性度量以进一步约束关联规则。项集的相关性度量［11］可定义如下:

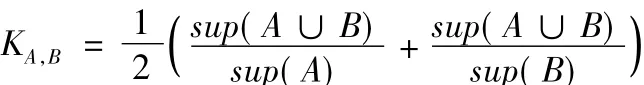
KA，B的取值范围为［0，1］:KA，B＞ 0．5 时 A 和 B 正相关;KA，B=0．5时 A和B相互独立;KA，B＜ 0．5时 A和B负相关。

定理1［7］项集A和B正相关时仅需挖掘AB和AB类规则;A和B负相关时仅需挖掘AB和AB类规则;A和B相互独立时不需挖掘规则。

定理1的实际应用中，通常会设正相关强度判定阈值k1和负相关强度判定阈值k2来降低挖掘出的规则数量和提取真正感兴趣的规则。由此可得相关度－支持度－置信度框架:1)获取满足正、负相关强度阈值的关联规则;2)提取满足ms和mc约束的强关联规则。

1．4 正负关联规则置信度间的关系

由前述负关联规则支持度和置信度的计算关系可知，正负关联规则置信度的计算均与规则的项集支持度紧密相关，并且四种正负关联规则的置信度间还有如下约束关系成立:

对四种正负关联规则的置信度取值范围的研究有助于更合理地确定有效关联规则的置信度阈值。为此，文献［8］给出了基于项集支持度的规则置信度取值范围界定规律。

定理3 四种正负关联规则置信度取值范围:

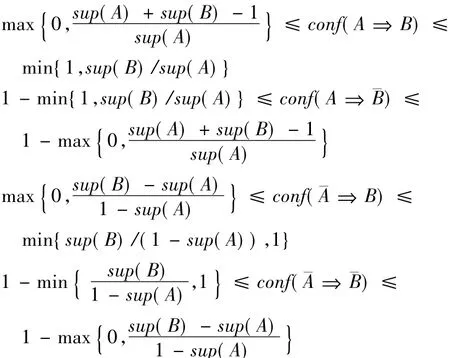
定理2表明，四种关联规则置信度之间存在互补关系。定理3表明，规则置信度取值范围的确定与规则的项集支持度紧密相关，且在不同项集支持度取值下规则的置信度取值范围存在差异。显然，单级置信度阈值难以有效反映四种规则置信度间的约束关系，也没有考虑四种规则置信度间的差异。而四级置信度阈值法又无法反映四种规则置信度间变化的有机联系。鉴于此，两级置信度阈值法更为合理。

2 结合项集相关性的两级置信度阈值设置法

文献［7，10］的双置信度阈值法假设四种关联规则同时挖掘，且它们的置信度阈值满足定理2的约束;但是，根据定理1，在考虑项集A和B相关性后，AB和AB、AB和AB不会同时出现。实际上，在相关度－支持度－置信度框架下，文献［7，10］提出的双阈值法是无法有效限制低可信度规则数量的，并且还容易遗漏一些有趣规则，因此，本文结合规则的项集相关性，以定理3为基础，分析了正负关联规则置信度的变化特点，有如下结论:关联规则的项集正相关时，规则置信度高低变化趋势与规则的项集支持度大小变化趋势有关;关联规则的项集负相关时，规则的置信度高低变化趋势与规则的项集支持度间的差距大小有关。据此，本文提出了一种新的两级置信度阈值设置方法。新方法包括正负关联规则的两个置信度阈值，其设置还涉及相关强度判定阈值k1和k2以及规则的项集支持度差距阈值εmin。

2．1 正负关联规则置信度变化特点分析

情形1 sup(A)+sup(B)≤1且sup(B)≥sup(A)。

情形2 sup(A)+sup(B)≤1且sup(B)＜sup(A)。

情形3 sup(A)+sup(B)＞1且sup(B)≥sup(A)。

情形4 sup(A)+sup(B)＞1且sup(B)＜sup(A)。

情形1的变形推理过程如下:

因为sup(A)+sup(B)≤1

由此可得表1中情形1所示结果。情形2、3、4的变形过程与情形1类似。

表2是由定理3得出的几种典型sup(A)和sup(B)取值下四种关联规则置信度的取值范围示例。

文献［8］在分析四种规则置信度的特点时仅考虑了sup(A)和sup(B)都大于0．9、sup(A)和 sup(B)都小于0．1等特殊情形。为了提高新两级置信度阈值法提取规则的有效性，本文以表1为基础，结合关联规则的项集相关性及表2中的实例，分析四种正负关联规则置信度变化的一般特点。

(1)sup(A)和sup(B)都偏小时令sup(A)+sup(B)≤1。对情形1，有conf(AB)∈［0，1］，conf(AB)的左边界→1－sup(A)/(1－sup(A))=1－1/(1/sup(A)－1)，因sup(A)偏小，故conf(AB)左边界偏高;对情形2，conf(AB)右界→1，即conf(AB)∈［0，1］，而conf(AB)左边界→1－1/(1/sup(B)－1)，因sup(B)偏小，故conf(AB)的左边界偏高。

(2)sup(A)和sup(B)都偏大时令sup(A)+sup(B)＞1，此时，情形3和情形4的conf(AB)左边界都为1+sup(B)/sup(A)－1/sup(A)→2－1/sup(A)，因为sup(A)＜1且sup(A)偏大，故1/sup(A)→1+，2 －1/sup(A)→1－，可见，conf(AB)偏高。对conf(AB)，当ε→0时都有conf(AB)∈［0，1］。

综上，项集A和B正相关时，若sup(A)和sup(B)都偏小，conf(AB)可高可低，但conf(AB)偏高。如表2中1、2行的第5～6列所示;若sup(A)和sup(B)都偏大，conf(AB)偏高，conf(AB)可高可低。如表2中3、4行的第5～6列所示。

表1 不同sup(A)和sup(B)情形下的正负关联规则置信度的取值范围Tab．1 Confidence range of positive and negative association rules in different sup(A)and sup(B)situations

表2 不同sup(A)和sup(B)取值下的正负关联规则的置信度取值范围示例Tab．2 Examples of confidence range of positive and negative association rules in different values of sup(A)and sup(B)

当sup(A)+sup(B)→1且ε→0时，有:

max{0，(sup(A)+sup(B) －1)/sup(A)}→0

min{1，sup(B)/sup(A)} →1

max{0，(sup(B)－sup(A))/(1－sup(A))}→0

min{sup(B)/(1－sup(A))，1}→1

(1)对于情形1。

(2)对于情形2。

(3)对于情形3。

(4)对于情形4。

综上，项集A和B负相关时，若sup(A)+sup(B)→1且ε偏小，两种规则的置信度可高可低。此外，有:ε越大(小)，AB和AB中一类规则的置信度越高(低)，而另一类规则的置信度可高可低。如表2中最后两列所示。

2．2 两级置信度阈值设置法PNMC-TWO

由上一节的讨论可知:A和B正相关且支持度偏小时conf(AB)可高可低，但conf(AB)偏高;A和B正相关且支持度偏大时conf(AB)偏高，conf(AB)可高可低。考虑到AB类规则与可信度低的AB类规则实用性不强［10］，此时可通过设置高置信度阈值(mc-max)来降低AB类规则数量并保证AB类规则的高可信度。

A和B负相关时，若sup(A)+sup(B)→1且项集支持度差距ε偏小，conf(AB)和conf(AB)都是可高可低，此时，为了有效防止有趣关联规则的遗漏，算法可设置低置信度阈值(mc-min)加以保证。

综上，正负关联规则两级置信度阈值法(PNMC-TWO)的设置思想如下:设mc-min为低置信度阈值，mc-max为高置信度阈值。从事务数据库D中筛选出满足项集相关性强度阈值的项集A和B。若A和B正相关，AB和AB类规则的置信度阈值用mc-max。若A和B负相关，AB和AB类规则的置信度阈值设置分两种情形:ε＜εmin时用mc-min，ε≥εmin时用 mc-max。

正负关联规则挖掘一般分为两个步骤:1)找出事务数据库D中满足用户要求的所有项集;2)由项集产生强关联规则。PNMC-TWO用于正负关联规则提取阶段，下面给出该阶段的伪代码。

算法 用PNMC-TWO提取有趣正负关联规则。

输入 需要进行相关性分析的项集集合U，正相关强度阈值k1和负相关强度阈值k2，两级置信度阈值mc-min和mc-max，项集支持度差距阈值εmin，支持度阈值ms。

输出 正负关联规则集合PAR和NAR。

2) while(each itemset A，B∈U and A∩B={

3) if(KA，B≥k1){

8) if(KA，B≤k2){

14) else{

19) } //if k2

20)} //while

21)return PAR and NAR

设U中项集个数为n，则算法在最坏情况下的时间复杂度为O(n2)。使用PNMC-TWO时的算法步骤3)～18)时间复杂度为O(1)，说明新方法的使用不会额外增加用户所选择的正负关联规则挖掘算法的时间开销。PNMC-TWO置信度阈值设置法融合了4种正负关联规则的置信度取值变化规律，使得两级置信度阈值的设定变得更为客观和科学，更具一般性和适应性，有利于有效规则的提取。

3 实验分析

为检验PNMC-TWO的有效性，本文以文献［15］的正负关联规则挖掘算法为统一模型，采用文献［11］提出的最优相关度量KA，B，与文献［7，10］的正负关联规则双置信度阈值法进行了实验对比。

实验环境:Intel Core i5-5200U 2．20 GHz处理器，4 GB内存，Windows 10操作系统，Matlab R2015b编程。事务数据库:1)小型事务数据集［6］。它包含10个事务和6个项目;2)某超市某月的销售数据集。它包含747个事务，196个项，其中非频繁项集居多;3)UCI上的chess数据集。它包含3196个事务和75个项目，具有高度正关联的特点。

实验参数:表 3 中 k1=0．6，k2=0．3，ms=0．3，εmin=0．5。表4中k1=0．6，k2=0．3，ms=0．15，εmin=0．5。表5中k1=0．7，k2=0．3，ms=0．94，εmin=0．5。

在不同的置信度阈值下，两类双置信度阈值法在小数据集上的挖掘结果如表3所示，在超市数据集上的挖掘结果如表4所示，在chess数据集上的挖掘结果如表5所示。其中，P-mc表示文献［7，10］方法中AB和AB型规则的置信度阈值，N-mc表示文献［7，10］方法中AB和AB型规则的置信度阈值，且P-mc+N-mc=1;FAR表示两种方法提取出的正关联规则数量，NAR表示负关联规则数量。

表3 小数据集上挖掘规则数量及运行时间Tab．3 Number of mined rules and running time on small data set

表4 超市数据集挖掘规则数量及运行时间Tab．4 Number of mined rule and running time on supermarket data set

表5 chess数据集挖掘规则数量及运行时间Tab．5 Number of mined rule and running time on chess data set

从表3～5可知:当文献［7，10］双阈值法中 P-mc与PNMC-TWO中mc-max保持一致时，提取的正关联规则数量相同，这表明PNMC-TWO与文献［7，10］双阈值法在控制 AB型规则方面具有同样好的效果。但是，从表3和表4可观察到，PNMC-TWO提取出的负关联规则与原双阈值法提取出的负关联规则相比，数量明显减少。原因在于，文献［7，10］的双阈值法中，如果P-mc很高，N-mc就会很低，它使得大量无趣的低可信度AB和AB型规则被提取出。而PNMC-TWO由于考虑了规则置信度的内在变化规律，使之对负关联规则数量调控非常显著。它既不会遗漏掉有趣的关联规则，也不会产生过多低可信度的关联规则。可见，在控制规则数量和保证规则有趣方面，PNMC-TWO比文献［7，10］双阈值法更有效。

对chess数据集挖掘时所需进行相关性分析的项集对共有7574对，其中99%的相关度大于0．9，其余的不小于0．3，说明chess数据集中有趣项集间是高度正相关的，所以在P-mc和mc-max对应相同时，两个方法提取出的负关联规则(全为AB)数量相同，如表5所示。

可见，对具有不同大小和特点的数据集，PNMC-TWO都表现出了良好的有效性和适应性。另外，从运行时间来看，PNMC-TWO几乎不额外增加提取规则的时间开销。

4 结语

在相关度－支持度－置信度框架下，现有的正负关联规则置信度阈值设置方法挖掘出的规则质量不高。结合规则的项集相关性分析，在分析正负关联规则置信度变化特点基础上提出了一种更加科学、合理的PNMC-TWO。理论分析和实验计算表明，新方法能更加有效地控制挖掘出来的规则数量，同时还可以确保挖掘出来的规则是真正有趣的关联规则。