基于熵权Vague 集的多目标决策方法

赵庆庆，黄天民

(西南交通大学数学学院，成都611756)

(*通信作者电子邮箱Zhaoqingswjtu@163．com)

0 引言

1965年，Zadeh［1］首次提出了模糊集的概念，并在管理决策领域［2－3］、军事运筹学领域［4］、人工智能领域［5］等取得重大进展。1993年，Gau等［6］提出了Vague集理论，它是模糊集的推广形式，Vague集同时表示了支持和反对的证据以及未知程度，比模糊集向决策者提供了更多的信息。Chen等［7］将Vague集应用于多目标决策问题，通过定义一类计分函数或者加权计分函数得到决策结果，Hong等［8］以及李凡等［9］分别对文献［7］方法进行分析，针对不足之处给出修改形式。刘华文［10］在此工作的基础上，提出包含决策者犹豫度的计分函数与加权计分函数，并给出一种距离目标选择方法。然而在实际操作中，精确地表示一个元素属于某个集合的程度很难实现，把隶属程度用区间数表示有更大的灵活性，周珍等［11］和王会英等［12］等利用区间值Vague集对Vague集作了进一步拓展并将其应用于多目标决策领域。

目前的研究成果均在集中Vague集的运算法则、Vague集的相似性度量、方案的优选准则等理论或方法方面，关于目标的Vague值，即隶属度、非隶属度和犹豫度的计算没有相应的研究。王珏等［13］通过设定满意度下界和不不满意度上界计算方案的支持目标集，反对目标集和中立目标集确定方案的Vague估计值，最后利用评价函数进行排序，但这种方法主观性较强并且评价函数单一，当支持目标集和反对目标集相同时无法得出最优方案。为了改进目标权重的主观任意性，许多学者基于信息熵的理论研究问题，按照熵的思想，人们在决策中获得的信息的多少和质量是决定决策精度和可靠性的因素之一，所以熵在应用于案例的效果评价时是一个很理想的尺度，适用于确定权重的过程。戴厚平［14］对属性信息完全未知且属性值为区间直觉模糊数的多属性决策问题进行了研究，提出基于信息熵的区间直觉模糊多属性决策方法。黄松等［15］利用熵权系数法计算权重，并通过专家给出每个目标的满意度下界和不满意度上界得出各个目标的平均满意度下界和不满度上界，若用此方法对目标过多的方案排序，会增加专家的工作量，降低决策效率。熵权法计算出的目标权重具有客观性，但是研究者在利用熵权法进行多目标决策时，往往只考虑客观权重，忽略了人的主观偏好。

基于以上的问题，本文重新定义了评价函数，并综合考虑客观权重和主观权重得到各个目标的权重向量区间，通过计算方案的支持目标集和反对目标集得到方案的Vague估计值，最后利用新的评价函数进行排序。另外还将该方法与文献［13］方法作了比较，表明该方法更为合理和有效。

1 预备知识

假设有n个备选方案，m个目标，n个备选方案对m个目标的指标值构成决策矩阵

表示成矩阵的形式为:

多目标决策的一般模型可描述:

其中fij表示方案xj的第i个目标值。

首先将决策矩阵F转化为目标优属度矩阵，通常采用如下方法确定目标的优属度μij:

对于效益型指标(目标值越大越好)

对于成本型指标(目标值越小越好)

对于效益型目标(目标值越接近某一固定值越好)

2 确定各目标的权重向量区间

2．1 熵权法确定目标的客观权重

熵是系统无序程度的一种度量，目前熵值的表示方法也有很多，一种是基于概率的表示，系统可能处于N种不同的状态，每种状态出现的概率为pi(i=1，2，…，N)，则评价该系统的熵可定义为:

或者利用三角函数定义直觉模糊熵，它主要考虑隶属度与非隶属度的偏差，设Y是一个论域，且

为X上的直觉模糊集，则xi的熵值定义为:

其中πA(x)=1－uA(x)－vA(x)。

因为要定义各个目标的客观权重，根据目标的确定性和便于归一化处理的特点，采用基于概率的方法确定目标的熵值。

定义1［14］第i个目标的熵值表示为:

熵是信息论中衡量不确定性的指标，信息量的分布越趋于一致，不确定性越大，则当μij/μi的值完全相等时，熵Ei的值达到最大:max Ei=ln m。容易看出:目标的信息熵越小，表明目标值的变异程度越大，提供的信息量越大，则其权重也应越大;反之，目标的信息熵越大，表明目标的变异程度越小，提供的信息量越小，则其权重也应越小。

定义2［14］差异程度越大的目标越重要，则可将目标的熵值取补后归一化处理得到目标i的客观权重:

各目标的客观权重向量

2．2 确定目标的权重向量区间

对于综合考虑客观权重和主观权重，人们往往采取线性加权法，这样会丢失掉一些有用信息，针对这一缺陷本文重新定义了权重区间的概念。

定义3 已知由熵权法得到的客观权重向量w'=(w1'，w2'，…，wm')，由专家确定的主观向量 w″=(w1″，w2″，…，wm″)，目标的权重向量区间定义为:

3 Vague估计值和评价函数的确定

3．1 计算方案的Vague估计值

定义 4［13］设 f(x)=(f1(x)，f2(x)，…，fm(x))Τ表示m个目标的向量。

1)令λU是决策者能够接受的满意度下界，若μij＞λU，则称第j个方案支持第i个目标;

2)令λL是决策者能够接受的不满意度上界，若μij＜λL，则称第j个方案反对第i个目标;

3)若λL≤μij≤λU，则称第j个方案对第i个目标保持中立。

定义 5［13］

1)Fj=为第j个方案的支持目标集;i=1，2，…，m;j=1，2，…，n。

2)Aj=为第j个方案的反对目标集;i=1，2，…，m;j=1，2，…，n。

3)Nj=为第j个方案的中立目标集;i=1，2，…，m;j=1，2，…，n。

一般的，支持目标集中包含的目标越多越好。下面我们利用Vague集的相关理论进行Vague估计。

定义6 设权重区间

对方案xj∈X，它在m个目标上满足决策者要求的程度用Vague值V(xj)表示，即V(xj)=［t(xj)，1－f(xj)］，其中:

并且 i=1，2，…，m;j=1，2，…n。

3．2 评价函数的确定

定义7 设V(xj)是一个区间Vague值，V(xj)表示为:

定义评价函数s(xj)为:

容易看出，s(xj)∈［－1，1］。由上述定义可知，s(xj)的值越大，方案越满足决策者的要求，进而可以选出最优方案。

3．3 基于熵权Vague集的多目标决策算法

基于对上述理论和方法的分析，下面本文给出基于熵权Vague集的多目标决策方法的具体步骤:

步骤1 将决策矩阵转化为目标优属度矩阵;

步骤2 综合熵权法求得的客观权重和专家决定的主观权重转化为权重向量区间;

步骤3 根据定义求出每个方案的Vague估计值;

步骤4 利用评价函数对所有方案排序并选出最优方案。

4 算例

本文采用文献［17］的最佳防御要点选择问题，该问题中有5 个方案，6 个目标，即 X=(x1，x2，x3，x4，x5)，f=(f1，f2，f3，f4，f5，f6)，其中f1为成本型目标，f2为固定性目标，其余均为效益型目标，经过军事专家和指挥员评判，确定各个目标的权重向量为 w″=(0．24，0．18，0．18，0．12，0．12，0．16)，且决策矩阵如下:

步骤1 将决策矩阵F转化为目标优属度矩阵μ为:

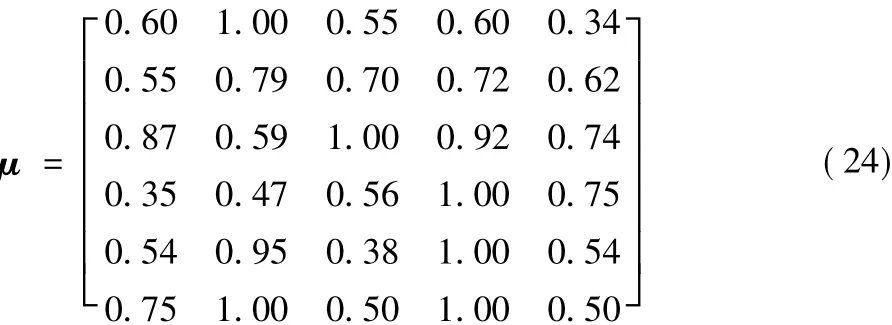
步骤2 求出每个目标的权重向量区间。

由熵权法求得每个目标的熵值为:

归一化处理得到各个目标的客观权重:

根据定义每个目标的权重向量区间为w:

步骤3 求出每个方案的Vague估计值

取 λL=0．75，λU=0．75，则各个方案的支持目标集、反对目标集和中立目标集分别为:

根据定义得到5个方案的Vague估计值:

步骤4 分别计算5个方案的评价函数值

s(x1)=0．011，s(x2)=0．524，s(x3)=0．011，s(x4)=0．643，s(x5)= － 0．194; 则得排序结果为 x4> x2> {x1，x3}>x5，最优方案为x4．按照文献［13］的排序方法，当λL=0．5;λU=0．75 时得到的排序结果为{x2，x4} > {x1，x3} >x5，并没有选出最优方案，显然本文的排序方法更加有效。

容易看出，当λL、λU取不同的值时排序结果不同，表1为不同的λL、λU的排序结果，表2为文献［13］的排序结果。

表1 本文方案排序结果Tab．1 Ranking result of the proposed scheme

分析表1、表2 的排序结果，当 λL=0．57，λU=0．93 时，本文选出的最优方案为x4，文献［13］的方法没有选出最优方案，λL，λU取其他值时，两种方法的排序结果相同，所以本文的排序方法是合理的并且更加有效;文献［16］提出一种决策方法，并且计算了 λL=0．57，λU=0．90 时的决策结果，得到的排序方案为x2> x4> x5> x3> x1，当 λL=0．57，λU=0．90时，本文决策方法的排序结果为x4>x2>x1>x3>x5，显然取 λL=0．57，λU=0．90 时，方案 x4更符合要求，取其他值时两种方法的决策结果相同，验证了文中方法更优;文献［17］是传统的决策方法，文中方法包含了文献［17］的方法，当取 λL=0．46，λU=0．93 时，得到的排序结果为 x2> x4>x3>x1>x5，此时的排序结果与文献［17］的极大极小法相同，决策者持悲观态度;当取 λL=0．00，λU=0．36 时，得到的排序结果与文献［17］的极大极大法相同，决策者持乐观态度。

表2 文献［13］中方案排序结果Tab．2 Raking result of the scheme in［13］

5 结语

本文提出一种基于熵权Vague集的多目标决策方法，提出权重区间的概念并且重新定义了评价函数，通过计算方案的支持目标集和反对目标集得出方案的Vague估计值，从而实现对方案的排序。本文方法可以兼顾决策者的主观偏好和客观信息，使决策结果接近实际情况。并且此决策方法它蕴含了极大极小法和极大极大法，有效避免了目标权重的主观任意性问题，计算实例表明了此方法的可行性和有效性。但是确定满意度的上、下界时具有随机性和任意性，所以满意度上下界取值问题仍待进一步研究。