基于Dijkstra算法的京津冀旅游交通线路优化研究

王 佳，赵宏丽

(燕山大学 a.经济管理学院，b.校园建设管理处 河北 秦皇岛 066004）

当前，京津冀已成为继“长三角”、“珠三角”之后的又一最具活力的经济增长极，3省市经济一体化进程已不断向纵深推进。3省市签署的规划、交通、旅游一体化合作协议，打破了长期以来在上述领域3地各自为战的格局，京津冀区域相互依存、资源共享、一体化发展取得实质进展，其中交通无障碍是区域旅游一体化的基础和保障。

旅游交通是为旅游者由客源地到旅游目的地的往返，以及在旅游目的地各处旅游活动而提供的交通设施及服务，其便利程度，是衡量旅游业发达程度的重要标志，在食、住、行、游、购、娱等旅游活动六大要素中，属于先决条件，对旅游活动能否顺利进行起着决定性的作用。对于游客来讲，立足于最小的时间与经济成本获得最多的旅游体验；对于旅游组织者来讲，立足于最小的组织成本与最大的效益，而如何使线路通达性与组织成本之间获得平衡，达到性价比最优，成为旅游交通系统优化的重要指标。本文基于运筹学中的Dijkstra算法，寻找最优化的旅游交通线路，实现3省市之间交通的无缝对接与交通的无障碍，促进旅游经济一体化进程的加速。

1 研究方法

1.1 Dijkstra算法

Dijkstra(迪杰斯特拉)算法于1959年提出，是典型的单源最短路径算法，多用于解决指定两点vs，vt间的最短路，或从指定点vs到其余各点的最短路,目前被认为是求无负权网络最短路问题的最好方法。Dijkstra算法一般的表述通常有两种方式，一种用永久性标号P和临时标号T方式，一种是用OPEN,CLOSE表示的方式，本文采用永久和临时标号的方式。

1.2 研究思路

Dijkstra算法是基于以下原理：若序列｛vs,v1,…,,｝是从到的最短路，则序列｛vs,v1,…,vn-1｝是从到的最短路。

步骤如下：

（1）给 vs以 P 标号，P(vs)=0，其余各点均给 T 标号，T(vi)=+∞。

（2）若 vi点为刚得到 P 标号的点，考虑这样的点 vj：（vi，vj）属于E，且vj为T标号。对vj的T标号进行更改：T(vj)=min[T(vj),P(vi)+lij]。

（3）比较所有具有T标号的点，把最小者改为P标号，即：P)=min[T(vi)]，当存在两个以上最小者时，可同时改为标号。若全部点均为P标号则停止。否则用代vi转回。

2 研究过程

2.1 研究的数据

本文研究的京津冀各城市以交通线路节点表示，各个节点的代码见表1所示。各城市间的线路距离数据见表2所示：

2.2 Dijkstra算法求解节点之间的最优路线

表2 京津冀旅游交通线路距离矩阵 单位：（km）

下面用Dijkstra算法求解京津冀各城市间的旅游交通线路的最短路，使游客在游览时用最少的时间，最小的成本，获得最多的旅游体验；使旅游组织者花费最少的组织成本，获取最大的旅游利润。下面以求v11（邯郸）节点到v4（秦皇岛）节点的最短路，即寻求v11到v4的最优线路为例来研究本文的核心问题。

(1)首先给 v11以 P标号，P(v11)=0，给其余所有点以 T标号。

(2)由于(v11,v10),(v11,v9),(v11,v7),(v11,v12)边属于 E，且 v9，v10，v7，v12为T标号，所以修改这四个节点的标号：

(3)比较所有T标号，T(v10)最小，所以令P(v10)=59。并记录路径(v11,v10)。

(4)v10为刚得到的P标号的点，考察边(v10,v1),(v10,v9),(v10,v13)的端点v1,vq,v13

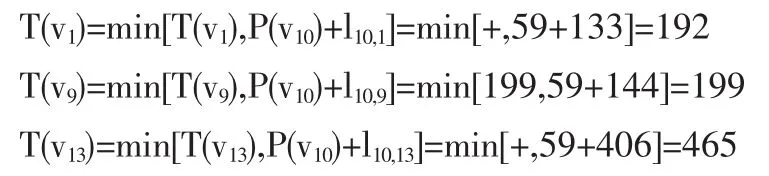
(5)比较所有T标号，T(v1)最小，所以令P(v1)=192。并记录路径(v10,v1)。

(6)v1为刚得到的P标号的点，考察边(v1,v3),(v1,v7),(v1,v8),(v1,v9)的端点 v3，v7,v8,v9。

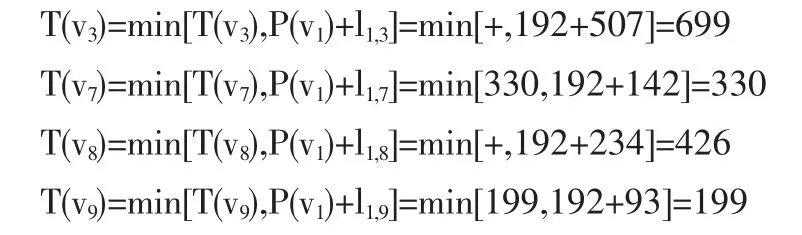
(7)全部T标号中，T(v9)最小，所以令P(v9)=199。并记录路径(v11,v9)。

(8)v9为刚得到的P标号的点，考察边(v9,v7),(v9,v12),(v9,v13),(v9,v8)的端点 v7,v12,v13,v8。

(9)比较所有T标号，T(v7)最小，所以令P(v7)=330。并记录路径(v11,v7)。

(10)v7为刚得到的P标号的点，考察边(v7,v3),(v7,v12),(v7,v5),(v7,v13),(v7,v8)的端点 v3,v12,v5,v13,v8。(11)比较所有T标号，T(v8)最小，所以令P(v8)=342。并记录路径(v9,v8)。

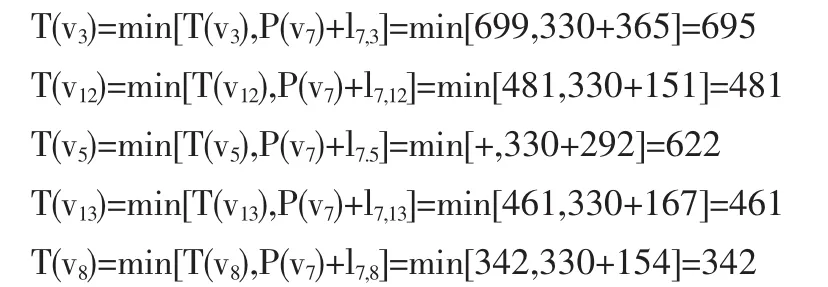
(12)v8为刚得到的P标号的点，考察边(v8,v12),(v8,v13)的端点v12,v13。

(13)全部T标号中，T(v13)最小，所以令P(v13)=461。并记录路径(v9，v13)。

(14)v13为刚得到的P标号的点，考察边(v13,v2),(v13，v5)的端点v2,v5。

(15)全部T标号中，T(v12)最小，所以令P(v12)=481。并记录路径(v11，v12)。

(16)v12为刚得到的P标号的点，考察边(v12,v2),(v12，v6)的端点v2,v6。

(17)全部T标号中，T(v6)最小，所以令P(v6)=537。并记录路径(v12，v6)。

(18)v6为刚得到的P标号的点，考察边(v6,v2),(v6，v5)的端点v2,v5。

(19)比较所有T标号，T(v5)最小，所以令P(v5)=586。并记录路径(v13,v5)。

(20)v5为刚得到的P标号的点，考察边（v5，v4)的端点v4。

(21)全部T标号中，T(v3)最小，所以令P(v3)=695。并记录路径(v7，v3)。

(22)v3为刚得到的 P 标号的点，考察边（v3，v2)，（v3，v4)的端点 v2，v4。

(23)比较所有T标号，T(v2)最小，所以令P(v2)=710。并记录路径(v12,v2)。

(24)考察 v2。

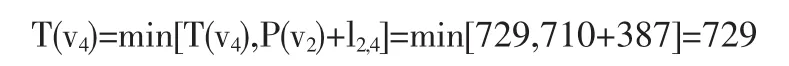
(25)因只有一个 T标号 T(v4)，令P(v4)=729，记录路径(v5,v4)，至此全部交通节点均为P标号，计算结束。按逆推法得到v11到 v4的最短路径为 v11→v9→v13→v5→v4，线路长 P(v4)=729。全部计算结果见图2，图中粗线为v11到v4的最优路线。

同理得到 v1到 v4的最短路径为 v1→v7→v13→v5→v4。

2.3 京津冀旅游交通线路优化的建议

完善的旅游交通体系是发展旅游业的必要前提。现今旅游业的蓬勃发展，特别是旅游旺季，给现有的旅游交通带来了一定的压力。压力的来源之一就是现有的交通线路设置不尽合理，没有考虑到游客对旅游交通的实际需求。创造便于游览、舒适、快捷、安全的旅游交通条件，以及“旅速游短，旅短游长，旅中有游，游旅结合”的旅游交通环境，满足游客的需求，实现良好的社会效益。

（1）构建一体化的旅游圈。构建一体化的京津冀旅游圈层结构，其中包括大旅游圈、旅游亚圈和重点旅游城市建设，使得各区域旅游业协同发展，为扩建旅游地空间结构提供条件。同时，形成合并旅游空间一体化，重塑新型旅游区域关系，实现“多赢”的区域旅游发展格局。

（2）设计合理的旅游线路。京津冀区域内旅游线路的设计应根据游客的旅游动机和切身利益来设计，同时还受到其他一些因素的影响，比如，各旅游节点之间的直接通达性、游客使用的交通工具及旅游出行规律等都会影响旅游线路的规划和设计。因此，应根据最优化线路设计原则，统筹设计合理的旅游线路。

（3）构造一体化的京津冀交通网络。原有的京津唐地区的天津到唐山的路线，需绕塘沽，加大了天津到唐山之间的交通成本和时间成本，为使津唐间的交通更便捷，必须要打通北辰到宁河间的路线；京津保地区的路线自霸州向南，依次经过任丘、肃宁、深州、饶阳和衡水，就会加大京津的经济辐射作用。京津冀交通线路的优化会使本区域内的经济格局由原来的带状分布演变为网状分布，从而加速了京津冀旅游经济一体化的进程。

3 结论

交通网络中的任意两交通节点间的最优路径都可以用Dijkstra算法求到。诚然，寻找最优的交通线路路径主要是解决旅游交通网络中的两节点之间的直达路径，若旅游组织者在组织旅游路线时倘若不考虑所经路径内的其他节点旅游资源性质，可以完全选择此最优路径，节约组织成本，耗费最短时间，达到最佳旅游效果。若考虑所经路径内的其他节点资源，就应考虑其他因素选择最优路线。本文引入Dijkstra算法，得到了京津冀经济圈内任意两旅游城市的最优交通线路，为实现京津冀旅游经济一体化、交通一体化奠定了理论上的基础。

[1]胡运权.运筹学教程（第三版）[M].北京:清华大学出版社,2007.

[2]保继刚，楚义芳.旅游地理学[M].北京:高等教育出版社,1999.

[3]王恒，李悦铮.大连市旅游交通空间结构分析与优化[J].海洋开发与管理，2009,（9）.

[4]鲍捷，陆林，吉中会.基于最小生成树Kruskal算法的皖北地区旅游交通优化与线路组织[J].人文地理，2010,（3）.

[5]张聪，但文红.黔东南州旅游交通通达性研究[J].重庆科技学院学报（社会科学版），2009,（1）.

[6]吴凯.旅游线路优化中的运筹学问题[D].东北财经大学硕士学位论文，2003.

[7]翁钢民.基于SOM网络的城市居民旅游需求区域差异研究[J].统计与决策，2007，（24）.