一个不等式试题的研究

●王红权 潘一力 (杭州市第十四中学 浙江杭州 310006)

在2010年浙江省第1次五校联考自选模块试题(简称1B试题)中，“数学史与不等式选讲”模块的试题是：

笔者经研究发现，该试题有多种解法，并得到了推广后不等式的上界和下界，现整理如下，供同行参考.

证法1 (分析法)设a+4b=t，则原不等式等价于

式(1)显然成立.

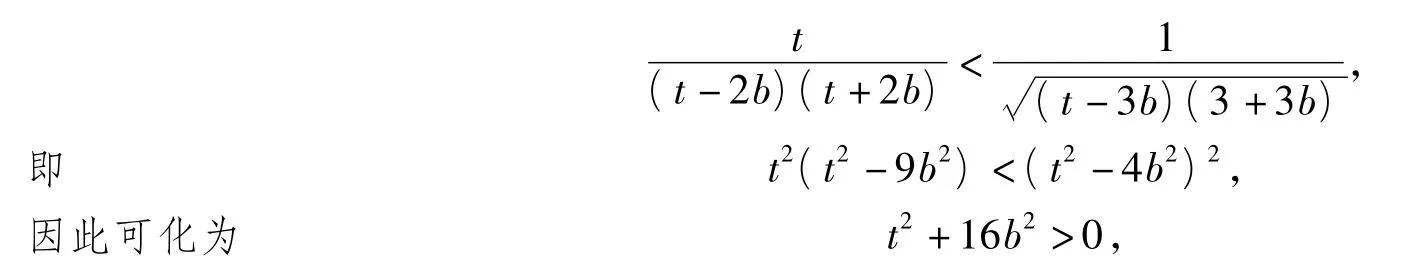
显然成立.令 t=a+4b，得

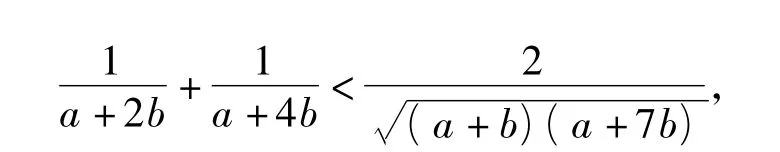
又由均值不等式知

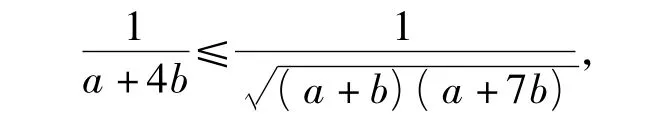
上述2个式子相加即得所证不等式.

证法3 (利用Cauchy不等式)因为

笔者研究发现，该不等式可推广为命题1.

命题1 对任意的正数a，b，有

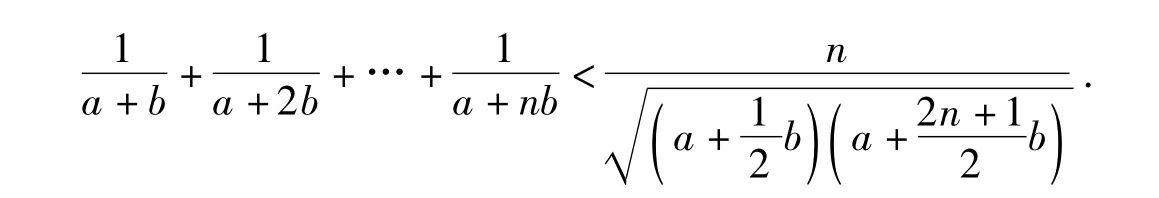
(2008年浙江大学自主招生数学试题)

证明由Cauchy不等式知

宁波大学陈计老师把该不等式加强为：

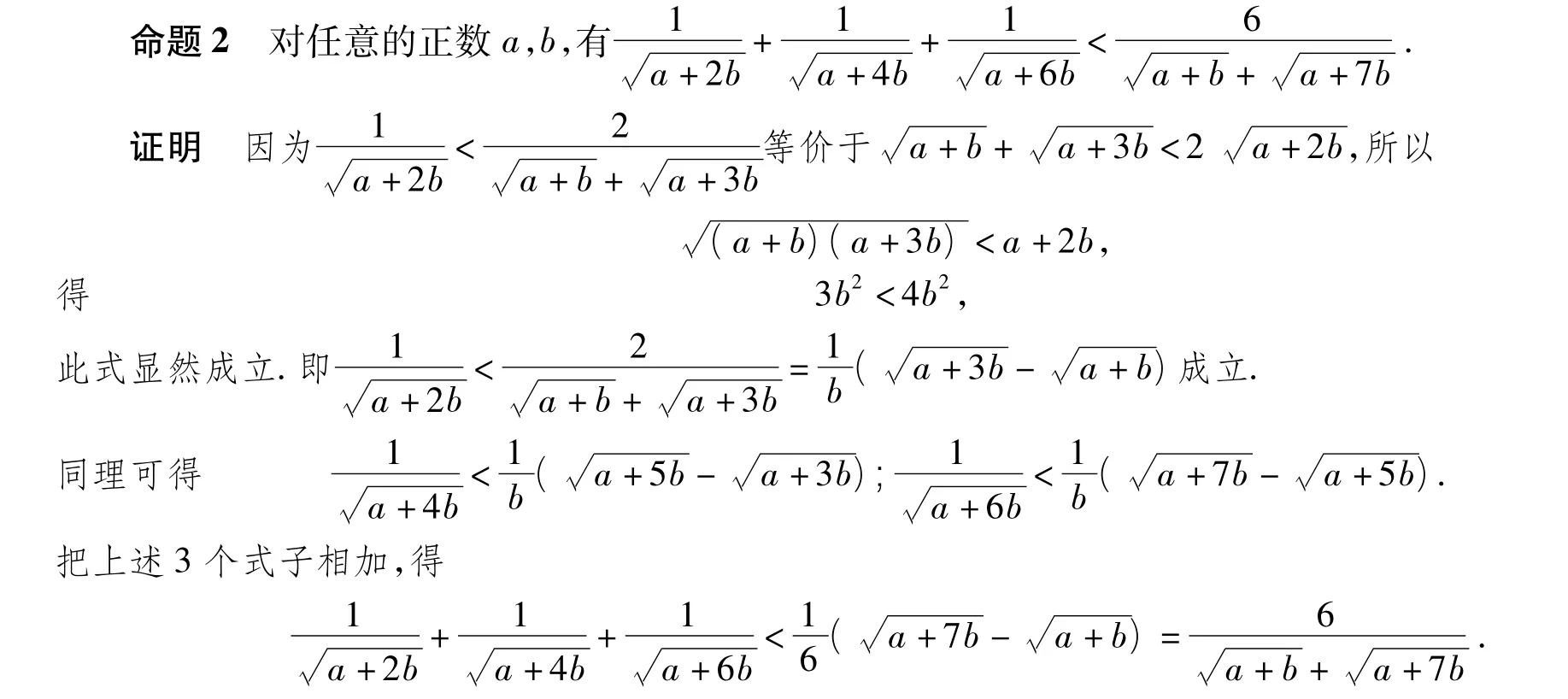
根据命题2的证明，容易推广得到

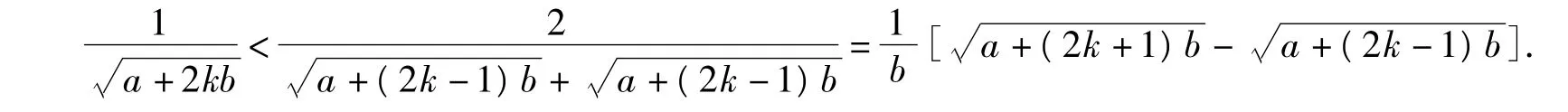
于是又得到如下推广.

命题3 对任意的正数a，b，n∈N+，有下面不等式成立：

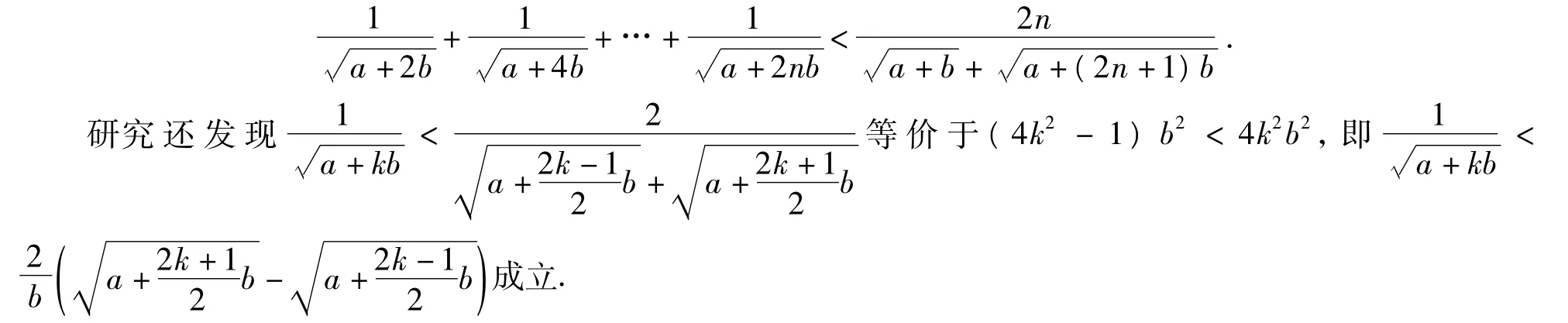
命题4 对任意的正数a，b，n∈N+，有下面不等式成立：

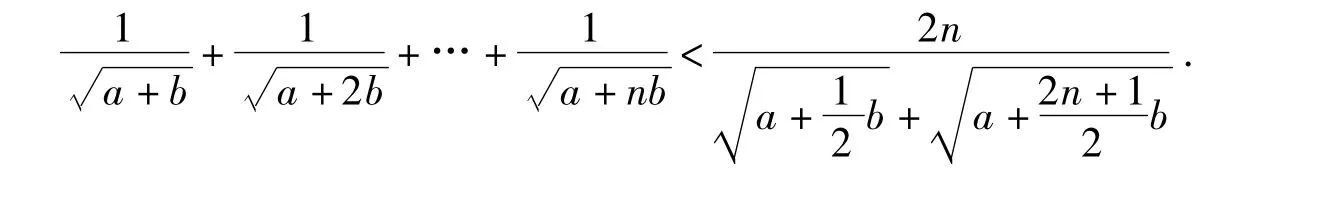
笔者在研究过程中，曾得到：

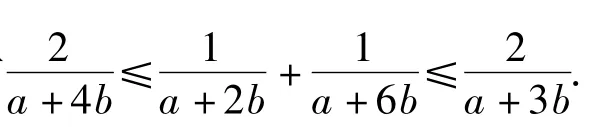
前面等号当且仅当b=0时成立，后面等号当且仅当ab=0时成立.

推广到n元后，可得

命题6 对任意的非负实数数a，b(a，b不同时为0)和正实参数xi(i=1，2，3，…，n)，不等式

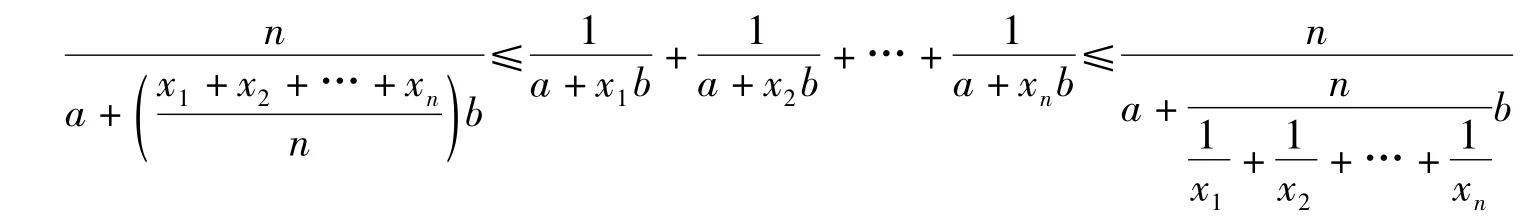
成立.前面等号当且仅当b=0时成立，后面等号当且仅当ab=0时成立.

证明不等式的左边可以由Cauchy不等式得到，下面只证不等式的右边.利用数学归纳法证明：

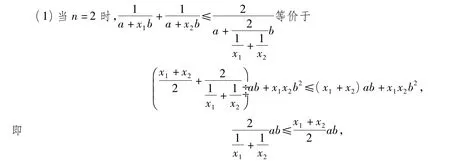
显然成立，且当ab=0时等号成立.

(2)假设当n=k(k≥2)时，命题成立，即

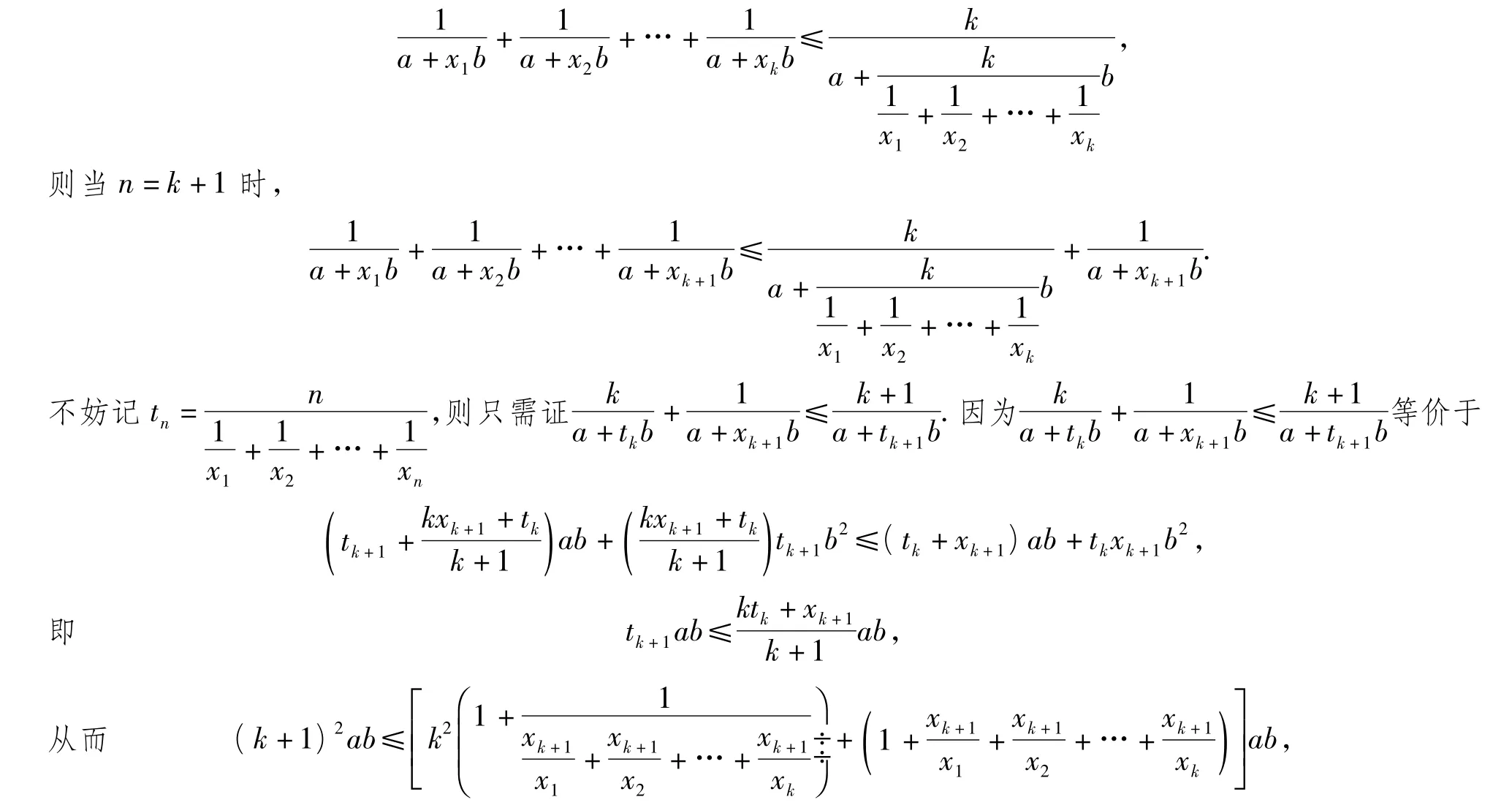
显然成立，且当ab=0时等号成立.故当n=k+1，命题成立.

综上所述，对任意的n≥2，n∈N+，原不等式都成立.