再谈“费马点”问题

443300 湖北省宜都市外国语学校 范 鸿

再谈“费马点”问题

443300 湖北省宜都市外国语学校 范 鸿

文［1］中，从怎样求线段的最值方面作了分类解析，仔细研读，很受启发.笔者也非常关注“费马点”问题，读此文后觉得有一丝遗憾的是，作者没有谈到涉及“费马点”问题的旋转变换以及性质的运用.其实，在新课标人教实验版八年级《数学》上册P 42有一道探究题，稍加改动题中的措词，就会变为一个关于“费马点”的讨论问题，现提出来供大家交流.

1 课本中的“费马点”雏形

例1课标人教实验版八年级《数学》上册P 42的探究题：如图1，要在燃气管道l上修建一个泵站，分别··向A，B两镇供气，泵站修在管道的什么地方，可使所用的输气管线最短?

图1

解析分析题意，在这个问题中，“分别”的意思应该是铺设两条管道且彼此互不相关，即泵站向A镇供气不经过B镇，泵站向B镇供气不经过A镇.根据“两点之间，线段最短”公理，“分别向”就是“分别直接向”.如图2，作点A关于直线l的对称点A'，连接A'B，与直线l的交点P就是泵站的位置.

这正是文［1］中谈到的通过轴对称变换达到“化折为直”，回归到“两点之间，线段最短”，但这里有一个前提是题目条件中有“分别”的表述.

2 “费马点”的相关知识

2.1 费马点：指到三角形的三个顶点的距离之和最短的点

对于一个各角都小于120°的三角形，费马点是对各边的张角都是120°的点;对于有一个角大于或等于120°的三角形，费马点就是最大的内角的顶点.

图2

2.2 费马点的作图

以△ABC的各角都小于120°为 例，如 图 3，分 别 以△ABC的两边AB，AC为边长向形外作等边三角形，作这两个等边三角形的外接圆，则两圆的另一个交点P就是此三角形的费马点.

图3

2.3 费马点的性质

平面内一点P到△ABC三个顶点的距离之和为PA+PB+PC，当且仅当点P为费马点时，距离之和PA+PB+PC最小.

2.4 费马点的性质证明

如图 4，设 点 P是△ABC内的一点，将△APC绕点 A逆时针旋转60°，得到△AP'C'，连接 PP'，显然△APP'为等边三角形，则AP=PP'，P'C'=PC.

所以点C'可看成线段AC绕点A逆时针旋转60°而得到的定点，BC'为定长，所以当 B，P，P'，C'四点在同一直线上时，PA+PB+PC最小，此时∠APB=∠BPC=∠APC=120°.

以上费马点问题告诉我们，平面内存在这么一个点到三个定点的距离之和最小，解决问题的方法是运用旋转变换.

3 中考试题中的“费马点”

例2 (2009年浙江省湖州)若P为△ABC所在平面上一点，且∠APB=∠BPC=∠CPA=120°，则点 P叫做△ABC的费马点.

(1)若点P为锐角△ABC的费马点，且∠ABC=60°，PA=3，PC=4，则 PB 的值为＿ ;

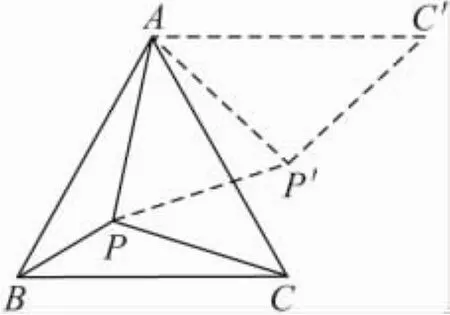
图4

(2)如图 5，在锐角△ABC外侧作等边△ACB'，连接 BB'.

求证：BB'过△ABC的费马点 P，且 BB'=PA+PB+PC.

解析(1)2

(2)设点P为锐角△ABC的费马点，即∠APB=∠BPC=∠CPA=120°.

如图5，把△ACP绕点C顺时针旋转60°到△B'CE，连接PE，则△EPC为正三角形.

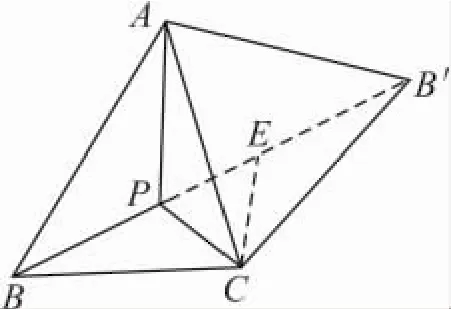
图5

例3 (2009年北京)如图6，在平面直角坐标系xOy中，△ABC三个顶点的坐标分别为 A(-6，0)，B(6，0)，C(0，4)，延长 AC到点 D，使CD=AC，过D点作DE∥AB交BC的延长线于点E.

图6

(1)求D点的坐标;

(2)作C点关于直线DE的对称点F，分别连接DF，EF，若过B点的直线y=kx+b将四边形CDFE分成周长相等的两个四边形，确定此直线的解析式;

(3)设G为y轴上一点，点P从直线y=kx+b与y轴的交点出发，先沿y轴到达G点，再沿GA到达A点，若P点在y轴上运动的速度是它在直线GA上运动速度的2倍，试确定G点的位置，使P点按照上述要求到达A点所用的时间最短.(要求：简述确定G点位置的方法，但不要求证明).

解析 (1)(2)略，对于第(3)问，如何确定点G的位置是本题的难点.

图7

就是MQ+AQ+BQ最小，就是在直线MO上找点G使它到A，B，M三点的距离之和最小.

这就是一个“费马点”问题的变形，注意到题目中等边三角形△MAB，考虑作旋转变换.

如图8，把△MQB绕点B顺时针旋转60°，

得到 △M'Q'B，连 接QQ'，MM'，可 知 △QQ'B，△MM'B都是等边三角形，则QQ'=BQ.

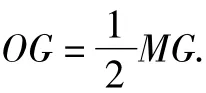
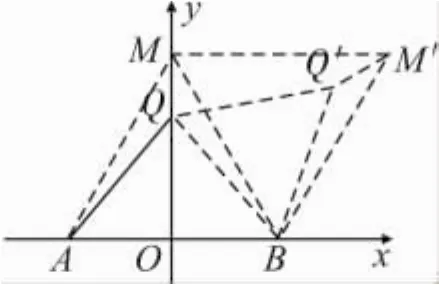
图8

注 例2是有关“费马点”的知识阅读理解，例3是有关“费马点”的转化运用，两例方法的共性在于运用旋转变换将问题转化到公理“两点之间，线段最短”上来，值得总结.

特别是例3，考虑到要使MQ+2AQ最小，就是MQ+AQ+BQ最小，即在直线MO上找到一点G使它到A，B，M三点的距离之和最小.我们可以直接运用“费马点”的定义和性质来解决这个问题.因为△MAB是等边三角形，所以点G一定在OM上，并且就是等边△MAB的外心，即点G是∠MAB的平分线与OM的交点，显然这样来解非常快捷.

现行初中教材没有提到“费马点”概念，更谈不上直接运用“费马点”的性质来解决路径最短问题，但讲清“费马点”的存在，其性质的由来以及为什么要进行旋转变换，对开拓学生的思维、提高学生的数学素质无疑是有益处的.如果掌握了“费马点”的性质并会灵活运用，那将大大提高解题的速度和质量.

由条件可以证明点Q'总在AM'上，所以 AM'与 OM 的交点就是所要的G点，如图9，可证

图9

1 李玉荣.从费马点谈起［J］.中学数学，2011，2(下)

2 金建华.费马点与中考试题［J］.初中数学教与学，2010，9

3 宋凡忠.费马点与最短路径［J］.中小学数学，2010，11

20110710)