三角函数最值问题及其应用——例谈高三数学第二轮复习的有效选题

211100 江苏南京东山外国语学校高中部 柳发志 郭 俊

三角函数最值问题及其应用
——例谈高三数学第二轮复习的有效选题

211100 江苏南京东山外国语学校高中部 柳发志 郭 俊

高三数学第二轮复习的主要目标应是引导学生将所有高中数学知识和方法系统化、网络化，熟悉知识间的联系，掌握分析解决问题的一般思维方法，进一步领悟数学思想方法，明确“考什么”、“怎么考”，及时发现在前阶段的复习中哪些知识点和方法技能掌握不牢固，哪些地方复习还不到位，做好查漏补缺、巩固提升，第二轮复习一般以专题的形式，主干是解题训练，以此提高学生的解题能力.显然，学生解题能力的形成，并不取决于解题数量的多少，而与题目的质量有密切的关系，因此要想取得复习效益最大化，教师精选例习题显得尤为关键，下面以“三角函数最值问题及其应用”这一专题谈谈笔者对第二轮复习有效选题的一些思考.

“三角函数最值问题及其应用”是高考中的重点考查内容之一，也是第第一轮复习的重点内容之一，那么第二轮复习中还应做些什么呢?应该说，此时的复习要做到减少与第一轮的重复，选题应重点突出，针对性强，注重知识的整合、方法的梳理，根据学生现状，让更多的学生感到有新意，有发展，有新收获，从以上思考出发，对这一专题采用系列题组教学，引导学生比较鉴别，进行方法、规律的归纳总结.

链接 (2010南京高三模拟)如图，现要在一块半径为1m、圆心角为60°的扇形纸板AOB上剪出一个平行四边形MNPQ，使点P在AB弧上，点Q在OA上，点M，N在OB上，设∠BOP=θ，平行四边形MNPQ的面积为S.

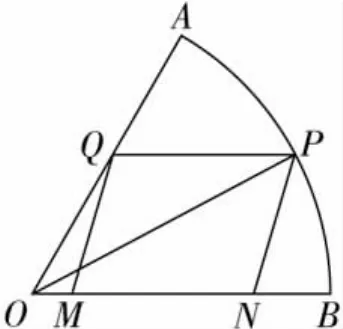
图1

(1)求S关于θ的函数关系式;

(2)求S的最大值及相应的θ的值.

点评 本例是三角函数最值问题中的常规典型问题，本质是研究运用函数y=Asin(ωx+φ)性质，学生比较熟悉，选取此例指导学生扎实抓好基础落实，熟练把握解题思路，注意思维严谨，在以三角函数为模型的一些应用题中，常常在得到类似函数解析式后求解最值，链接中的应用题源于教材，是此类问题的代表，高考中也常常出现.

点评 本例与例1形式上有相似之处，通过比较发现差异，解法上也有较大差异，这儿，视cosx为变量，联想二次函数的性质，转化为二次函数最值问题，通过此例，也提示学生注意题设条件，灵活选择合适方法解题.

链接 (2008江苏高考)如图2，某地有三家工厂，分别位于矩形ABCD的两个顶点A，B及 CD的中点 P处.AB=20km，BC=10km.为了处理这三家工厂的污水，计划在矩形区域内(含边界)且与A，B等距的O点建污水处理厂，并铺设三条排污管道AO，BO，PO.记铺设管道的总长度为ykm.

(1)按下列要求建立函数关系式：

(ⅰ)设∠BAD=θ(rad)，将y表示成θ的函数;

(ⅱ)设OP=x(km)，将y表示成x的函数;

(2)请你选用(1)中的一个函数关系式，确定污水处理厂O的位置，使三条污水管道的总长度最短.

点评 本例在形式上再次变化，出现了分式，教材中未曾出现，求解时就要求学生能站在高处看问题，通过解析式的适当变形，可视sinx+cosx为一整体，通过换元，转化为一常见的分式形式的函数，可类比例2，但是如果解析式中两分子的系数不相同，这时还这样处理就比较困难了，因此，还可以将该函数视作一“普通的函数”，而不仅仅是“三角函数”，这时就联想到可以运用导数工具，先通过导数方法研究这一函数性质，再运用性质求解最值，链接中的问题一般选用(i)中得到的函数求解比较方便，也体现了解题方法的优化.

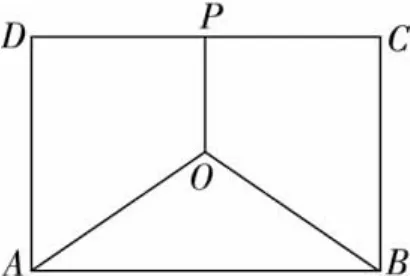
图2

点评 本例在例3的基础上再次变化，那么到底该选择怎样的解题思路与方法呢?注意到sin2x+cos2x=1及sin2x＞0，cos2x＞0，联想到基本不等式运用中的常见问题，就有了解法.这儿更多的是引导学生善于观察与发现，真正实现从数学运用的高度去思考，关注通性、通法，还要注意方法的优化.

对于这一专题为什么选用以上四例，下面再作简要说明.

1 专题复习还应低起点，抓落实

从例1出发，虽说学生对此类问题比较熟悉，但在熟练程度上是否已达到要求，在第二轮中还需整固，通过观察发现，明白解题根源，解题目标明确，能迅速将解析式进行变换转化，这儿也对三角变换做回顾与检查，另外，对题中出现角的范围约束是否已引起注意并能用好该条件，通过本例应该说可以对三角变换及三角函数性质运用整体上作回顾与整合.

2 专题复习必须多比较，重方法

例1与例2形式上类似，但实际上差别很大，审题时是否出现误读?通过比较，

是否能将二次函数知识与三角函数知识串联起来，快速合理切入解题?而到了例3、例4，又需要怎样去分析判断，怎样合理选择方法?这儿就要求学生能自觉从整个高中数学知识体系出发去思考问题解决方案，面对条件的变化，是否束手无策，能否克服困难?对学生的心理品质也提出要求.

3 专题复习必须成系统，高视角

1 石寅初.考试研究.南京：考试研究编辑部，2011，6

2 涂荣豹.数学之友.南京：数学之友杂志社，2010，4

20111128)