一堂探究性数学公开课的教学实录与评价

●

(宁波市职业技术教育中心学校 浙江宁波 315041)

一堂探究性数学公开课的教学实录与评价

●陈健

(宁波市职业技术教育中心学校 浙江宁波 315041)

《普通高中数学课程标准》中明确指出：“探究性课题学习是数学学习的一种新的尝试，其主要目的在于培养学生在数学上的创新精神，敢于质疑、提问、反思、推广，初步经历数学发现、数学探究、数学创造的过程，从而亲身体验数学探究的激情和愉悦”.笔者曾有幸听取了宁波市高一数学的一节公开课，主题是如何使用课本知识激发学生学习数学的热情，培养勇于探索和勇于创新的精神.选取的素材是一元二次方程根的分布，课题重点是一元二次方程根的分布情况，难点在于根的分布情况比较复杂，学生自行讨论、发现具有一定的难度，并且每一种分布情况的充要条件不易写出.现笔者把这一课堂教学实录及对其的评价整理如下,供参考.

1课堂教学实录

1.1 课题导入

教师：在初中阶段，我们学习了一元二次方程根的判别，请一位同学回答一下具体情况.

学生1：当Δgt;0时，方程有2个不相等的实根；当Δ=0时，方程有2个相等的实数根；当Δlt;0时，方程没有实数根.

教师：好.这说明大家对初中一元二次方程根的情况掌握较好,下面来看一个有关一元二次方程根的相关问题.

例1关于x的方程x2-kx+3-k=0.

(1)方程有2个正根，求实数k的取值范围；

(2)方程有2个负根，求实数k的取值范围；

(3)方程有1个正根1个负根，求实数k的取值范围.

学生根据已有的知识得到了如下解法:

学生2：假设方程有2个实根x1，x2,则第(1)小题要满足的条件是Δ≥0,x1+x2=kgt;0,x1x2=3-kgt;0.

学生3:第(2)小题要满足的条件是Δ≥0,x1+x2=klt;0,x1·x2=3-kgt;0.

学生4:第(3)小题要满足的条件是Δgt;0,x1+x2=klt;0,x1·x2=3-klt;0.

学生4按照前面2个学生的思路首先考虑判别式之后，进而关注两根之和及两根之积，经过教师的引导发现此时两根之和的符号不能确定.

教师：同学们在解决这个问题时主要应用了根的判别情况和韦达定理，那么能否从函数图像的角度去解决呢？

学生开始议论，表现出了兴趣，因为这和初中阶段的考虑方法不同，给问题的解决提供了一种全新的思路，也为下面的讨论作了铺垫.

学生5：感觉不可以.

教师：靠感觉不行，数学靠的是严密的逻辑，当然感觉也是一种素质的体现，但你的感觉正确吗？

学生的兴趣渐浓，很多学生认为可以.

学生6：可转化为一元二次函数与x轴的交点问题.

教师：需要考虑哪些因素呢？

学生6：抛物线的开口、对称轴、根的个数.

教师：不错，还可以作哪些改进呢？我们说，二次方程的二次项系数始终可以转化为大于0的情况，因此抛物线的开口都可以转化为向上，看看还有哪些遗漏的因素？

从例1出发，具体分析需考虑的因素.由函数图像可得如下解答：

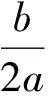
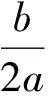
(3)Δgt;0,f(0)=3-klt;0.

经过师生共同探索发现,第(3)小题中不需考虑Δ,只要满足f(0)lt;0即可.

1.2 提出主题，学生探索

教师：刚才讨论了一元二次方程根ax2+bx+c=0(agt;0)的正负情况，并从函数图像的角度探讨了所要满足的条件.可以发现要考虑的条件包括Δ、对称轴位置和特殊点的函数值.实际上,二次方程根的分布还有很多种情况，请大胆探索.

学生经过讨论、探索，不断发现各种根的分布情况，教师在学生探索过程中巡视，了解学生的进展情况，发现在探索中遇到的困难，并根据实际情况适时加以引导.在整个过程中，学生都能积极思考，参与热情较高，现场气氛热烈.

1.3 成果展现

教师：下面请同学来展示讨论结果，假设x1，x2为方程的2个根.

学生7：2个根都大于2，即x1gt;2，x2gt;2．

教师：那此时的充要条件呢？

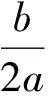
教师：很好.我们发现充要条件还是从Δ、对称轴位置和特殊点的函数值去考虑，这是解决问题的基本思路.还有其他情况吗？

学生8：2个根都小于2，即x1lt;2，x2lt;2．

教师：这个时候的充要条件呢？

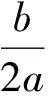
教师：不错.同学们找到了2种比较重要的分布情况.还有其他情况吗？我们回过来再看例题,实际上刚才2种情况是把0改为2，因此能否得到第3种情况呢？

学生9：一根大于2，另一根小于2.

教师：此时的充要条件又是什么？

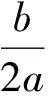
教师：大家看到这些条件可以推出方程的一根大于2一根小于2，由此可见它是方程的一根大于2一根小于2的充分条件，但是不是必要条件呢？刚才的条件有没有多余的呢？

学生开始思索，经过师生的共同探索逐渐排除了Δ和对称轴这2个因素.

教师：除了这3种情况,还有其他形式吗？刚才方程的根是和一个数比较，有没有可能是和2个数比较呢？

学生开始讨论，沉静的教室一下子就沸腾起来，带入了另一个探索的热潮.学生的想象力和创造力被激发出来，很多形式多样的分布方式浮出水面.

学生10：一根小于1，一根大于2，即x1lt;1,x2gt;2⟺f(1)lt;0,f(2)lt;0.

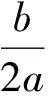
学生12：1lt;x1lt;2lt;x2⟺f(1)gt;0,f(2)lt;0.

学生13:x1lt;1lt;x2lt;2⟺f(1)lt;0,f(2)gt;0.

在教师的引导下，学生的思路进一步拓展，把方程的根与3个和4个数进行比较.譬如：1lt;x1lt;2lt;x2lt;3；1lt;x1lt;2,3lt;x2lt;4等.

1.4 教学小结

这节课主要探讨了一元二次方程根的分布情况，分布情况比较复杂，相应的充要条件难以把握.基本的方法是从二次函数图像的角度去考察，离不开几个重要的要素即根的判别、对称轴和特殊点的函数值等.主要讨论了几种重要的分布形式，可能还存在其他情况，希望感兴趣的学生可以在课后关注其他形式的根的分布情况.

2课后反思和评价

2.1 主线清晰，主题突出

课堂教学探索学习的2个最为显著的特征：其一是教学内容的问题化，即以问题为中心组织教学内容；其二是教学过程的探索化，即教师创设学习环境，由学生独立地探索发现知识和解决问题.本课在通过例题的引申和启发开展探索性学习，逐步展现一元二次方程根的分布情况，时刻围绕各种分布情况和相应的充要条件去开展探究活动，主线清晰、主题突出，是学生创新思维的出发点和生长点.

2.2 引导和探索的成功结合

探索性课堂教学的开展在很大程度上取决于学生的认知程度和能力水平，尽管我们都赞同探索性学习的重要意义，但在具体的实践过程中却存在着很大的难度，究其原因主要是探索中的不确定因素.这些因素主要来自于探索者即学生的认知结构和思维水平，以及对问题的关注和投入程度，这些因素直接影响着探索的程度和水平，也影响着探索性学习目的的实现.此外,课堂探索过程中又存在不定因素，譬如学生探索的方向原本明确，因为是自主探索，所以往往会偏离主题，相去甚远.在这个时候往往会产生学生突发奇想的事物,教师的引导和应变能力显得尤为重要和迫切.在本课中，教师显然已经做了大量的准备，根据学生的现实水平进行了精心的设计.首先对学生的认知水平有比较深刻的认识，对学生的思维能力有较为全面的估计，因此能够把握整个探索的进程；其次，对学生不能根据已有的知识进行探索的内容作及时而有效的引导和交流，使整个探索过程顺利而又热烈，并且积极调动一切有利于学生探索的条件和因素，使课堂气氛较为热烈，产生了良好的效果，同时促进了教师角色的更好发挥.我们认为，探索性课堂教学的成功莫过于教师的引导和学生自主探索的自然结合，相互渗透、辉映成彩.

2.3 处处体察皆探究

按照传统教学方法，教师将各种一元二次方程根的分布情况一一罗列出来，并根据每一种情况写出相应的充要条件，学生往往被动接受知识，体验不到探究带来的深切感受.学生对知识的认识只停留在表面，当然对问题的理解也停留在较低的水平，久而久之对知识的体系理解比较肤浅，更失去了对学生创新意识和创新能力培养的大好机会.我们深切赞同探究性学习对传统教学带来的重大变革，赞同探究性教学重要的现实意义和理论价值，但往往对内容的选择，形式的组织存在很大困惑.从本节课的感受来讲，探究的内容和形式无处不在、无时不可，关键在于如何去挖掘教材中的可探究之处.这就要求教师更新教育观念，注重学生的知识体验和探究能力的培养.教材中的很多基本内容都可作为探究的基本素材，处处都是探究的土地，处处是探究的乐园.在今后的课堂教学中,发挥教材的最大探究度将是我们值得关注和探究的重要内容.