三角形内切圆的几个性质及应用

●

(湖南师范大学数学奥林匹克研究所 湖南长沙 410081)

三角形内切圆的几个性质及应用

●沈文选

(湖南师范大学数学奥林匹克研究所 湖南长沙 410081)

本文将三角形内切圆中的几个有趣结论作为性质介绍如下.

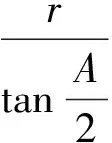
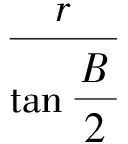
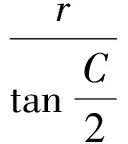
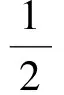
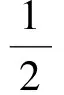
证明过程略.

性质2设△ABC内切圆的圆心为I，△IBC的外接圆分别和射线AB，AC交于点D，E，则DE与⊙I相切.

图1 图2

证明显然D，B，I，E，C五点共圆.对于图1，有

∠IDB=∠ICB,∠IDE=∠ICE.

而

∠ICB=∠ICE,

于是

∠IDB=∠IDE.

由于AD与⊙I相切，由对称性知DE也与⊙I相切.对于图2，有

∠IBC=∠IEC,∠IBD=∠IED,

而

∠IBC=∠IBD,

于是

∠IEC=∠IED.

因为EA与⊙I相切，所以ED也和⊙I相切.

性质3设△ABC的内切圆切边BC于点D，AD交内切圆于点L，过点L作内切圆的切线分别交AB，AC于点M，N，则

证明当MN∥BC时，△ABC为等腰三角形，此时结论显然成立.

当MN与BC不平行时(如图3)，可设直线MN与直线BC交于点G，设内切圆切AC于点E，切AB于点F，则

GD=GL,BD=BF,ML=MF.

对△GMB及截线DLA应用梅涅劳斯定理，得

从而

即

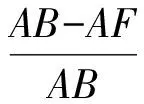
于是

同理对△GNC及截线CNA应用梅涅劳斯定理，可得

注意到AE=AF，于是

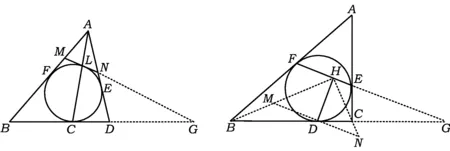
图3 图4

证明如图4，连结BH，CH.

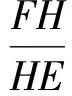
因为

∠BFH=∠CEH,

所以

△BHF∽△CHE,

于是

∠BHF=∠CHE,

且

由角平分线性质定理的逆定理，知DH平分∠BHC,从而

∠DHF=∠DHB+∠BHF=∠DHC+∠CHE=

∠DHE,

于是

DH⊥EF.

必要性当DH⊥EF时,若FE∥BC,则△ABC为等腰三角形,结论显然成立.若FE与BC不平行,则可设直线FE与直线BC交于点G(如图4).对△ABC及截线FEG应用梅涅劳斯定理,得

注意到AE=AF,BF=BD,CE=DC,得

过点D作MN∥HG交直线BH于点M,交直线HC于点N,则

DH⊥MN,

从而

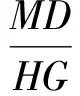
即

MD=DN.

由等腰三角形性质,知DH平分∠MHN,即

∠BHF=∠CHE.

又由

∠BFH=∠CEH，

得

△BHF～△CHE，

从而

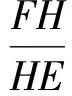
性质5设△ABC的内切圆⊙I切边BC于点D，P为DI延长线上一点，直线AP交BC于点Q，则BQ=DC的充要条件是点P在⊙I上.

证明如图5，过点P作B′C′∥BC交AB于点B′，交AC于点C′.

充分性当点P在⊙I上时，B′C′切⊙I于点P,易知△AB′C′∽△ABC.由于在∠BAC内它们的旁切圆分别为⊙I与⊙IA,因此在以A为中心的位似变换下，使⊙I变为⊙IA，此时切点P变为切点Q，即Q为直线AP与BC的交点.于是

BQ=p-c=DC，

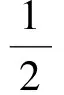
必要性当BQ=DC=p-c时，Q为△ABC的∠BAC的旁切圆的切点.由△AB′C′∽△ABC,可知存在以A为中心的位似变换，将BC上的点Q变为B′C′上的点P′，且P′为△AB′C′的∠BAC的旁切圆的切点.注意到B′C′∥BC,则点P′在过点D与BC垂直的直线上，从而点P′与P重合.故点P在⊙I上.

图5 图6

推论1设Q为△ABC的边BC上一点，则Q为∠BAC内的旁切圆的切点的充要条件是AB+BQ=AC+CQ.

性质6设△ABC的内切圆⊙I分别切边BC，CA，AB于点D，E，F，设K是DI延长线上一点，AK的延长线交BC于点M，则M为BC的中点的充要条件是点K在线段EF上.

证明如图6，过点K作ST∥BC交AB于点S，交AC于点T，则IK⊥ST.连结SI，FI，TI，EI.

充分性当点K在EF上时，注意到F，S，I，K及I，E，T，K分别四点共圆，得

∠ISK=∠IFK=∠IEK=∠ITK,

即△SIT为等腰三角形.

注意到IK⊥ST,知K为ST的中点.由于ST∥BC，因此M为BC的中点.

必要性当M为BC的中点时，K为ST的中点.由IK⊥ST,可得IS=IT,从而

Rt△ISF≌Rt△ITE,

即

∠SIF=∠TIE.

注意到F，S，I，K及I，E，T，K分别四点共圆，从而

∠SKF=∠SIF=∠TIE=∠TKE,

于是E，K，F三点共线，即点K在线段EF上.

推论2设△ABC的内切圆⊙I切边BC于点D，M为边BC的中点，Q为边BC上一点，则Q为∠BAC内的旁切圆的切点的充要条件是IM∥AQ.

事实上，参见图6，在证明充分性时，过点A作AQ∥IM交DI于点P，只要证得点P在⊙I上即可.在证明必要性时，延长DI交⊙I于点P，作直线AP交BC于点Q，证得IM∥AQ.

下面介绍几个应用的例子.

例1如图7，△ABC的内切圆分别切边BC，CA，AB于点D，E，F，M是EF上的一点，且DM⊥EF.求证：DM平分∠BMC.

(2005年江西省南昌市数学竞赛试题)

证明由性质4，得

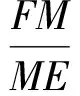
因为∠BFM=∠CEM,所以

△BFM∽△CEM,

即

∠BMF=∠CME,

由此可得DM平分∠BMC.

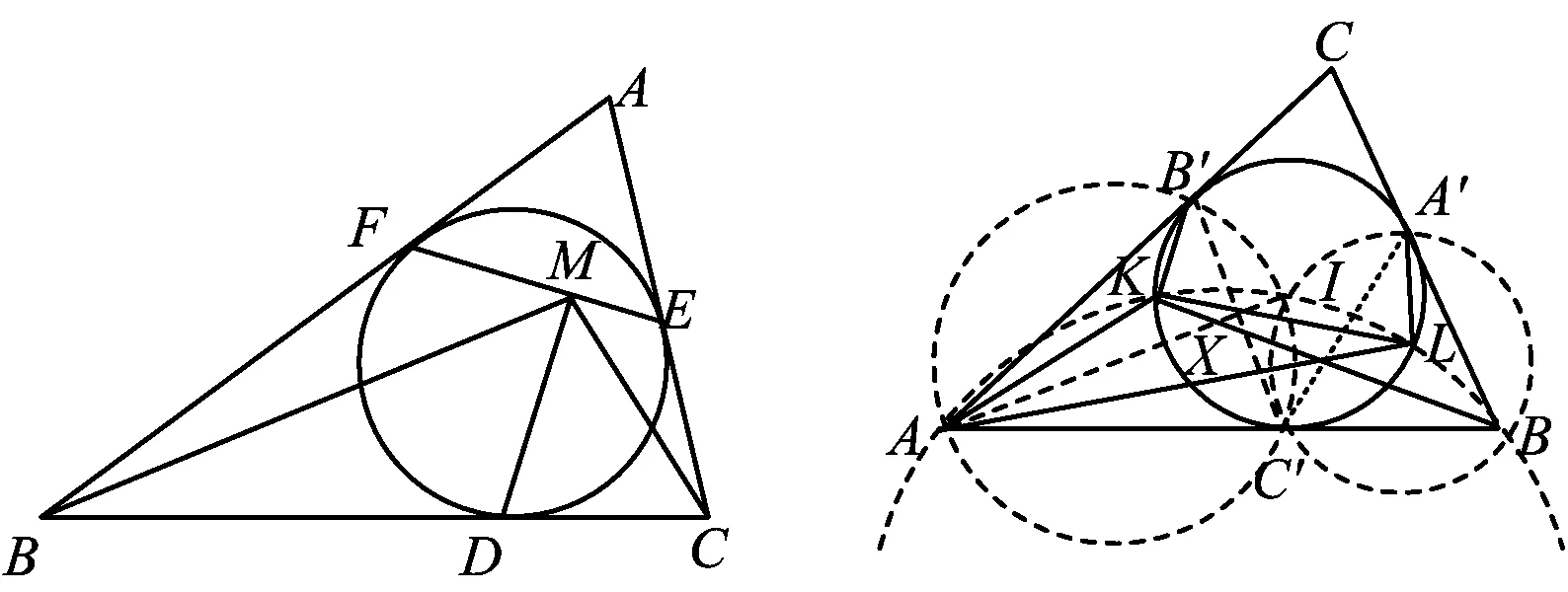
图7 图8

类似于例1，可推证《数学教学》1999年第3期数学问题481：已知△ABC的内切圆在边BC，CA，AB上的切点分别为D，E，F，且DG⊥EF，G为垂足，求证：GD平分∠BGC.

例2△ABC的内切圆W分别与边BC，CA，AB切于点A′,B′,C′，圆周上的点K，L满足

∠AKB′+∠BKA′=∠ALB′+∠BLA′=180°，

求证：点A′,B′,C′到直线KL的距离彼此相等.

(2008年第34届俄罗斯数学奥林匹克竞赛试题)

∠APB′+∠BPA′lt;∠A′PB′lt;180°，

∠AKB=180°-∠A′KB′=180°-∠A′LB′=

∠ALB,

从而A，B，L，K四点共圆.

连结B′C′,A′C′,由性质1(2)，得

∠AKB=180°-∠A′KB′=180°-∠A′C′B′=

从而A，B，L，I，K五点共圆.设AI与B′C′交于点X，则X为B′C′的中点.注意到B′C′,KL,AI分别为圆W，⊙AB′IC′，⊙AKILB两两的根轴，因而它们共点于X.因此，点B′,C′到KL的距离相等.

同理可得，点A′,C′到KL的距离相等.

例3设D为△ABC边BC上一点，且满足AB+BD=AC+CD,线段AD与△ABC的内切圆交于点X，Y，且X距点A更近一些，△ABC的内切圆与边BC切于点E.证明：

(1)EY⊥AD;

(2)XD=2IA′，其中I为△ABC的内心，A′为边BC的中点.

(2008年第10届香港特区数学奥林匹克竞赛试题)

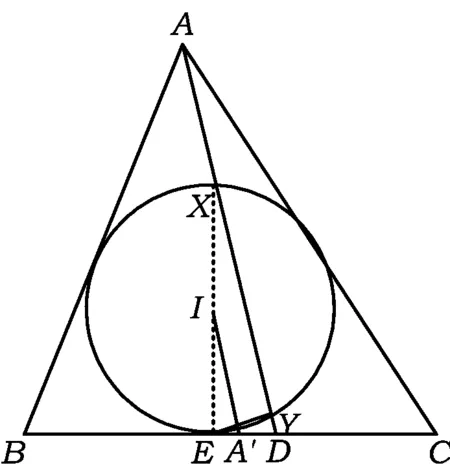
图9

证明(1)如图9，由推论1，知点D为∠BAC内的旁切圆与边BC的切点，再由性质5知XE为⊙I的直径，则∠XYE=90°，故EY⊥AD.

(2)由推论2，知IA′∥XD,而I为XE的中点，因此XD=2IA′.

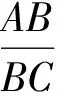
(2004年第18届韩国数学奥林匹克竞赛试题)

解由性质6，知Q为AC的中点.当点P在△ABC内时，如图10，在BQ的延长线上取点R，使QR=QP;取点S，使RS=AP.连结CR，AS，CS，则

CR=AP,PS=2PQ+AP=BP.

从而△ABS,△ACS,△RCS均为等腰三角形，则

∠QAP=∠QCR=∠RSA=∠ABQ,

从而

∠BAC=(90°-∠ABQ)+∠QAP=90°，

此时

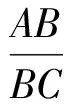
当点P在△ABC外时，如图11，作CR⊥BP于点R，则由Q为AC的中点知

CR=AP,RQ=PQ,

于是

BR=BP-2PQ=AP,

即△BCR为等腰直角三角形.此时，∠RCQ=∠PBA,从而

Rt△RCQ∽Rt△PBA.

由AB=AC=2QC,知AP=2QR=2PQ,于是RC=2PQ,从而

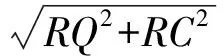
故

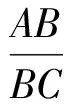
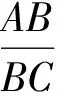
例5在锐角△ABC中，已知ABgt;AC，设△ABC的内心为I，边AC，AB的中点分别为M，N，点D，E分别在线段AC，AB上，且满足BD∥IM，CE∥IN，过内心I作DE的平行线与直线BC交于点P，点P在直线AI上的投影为Q.证明：点Q在△ABC的外接圆上.

(2010年中国国家集训队测试试题)

图12

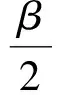
从而

设P1I与AC，AB分别交于点S，T，对△ABK及截线P1TI应用梅涅劳斯定理，得

因为

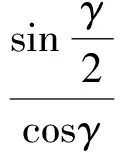
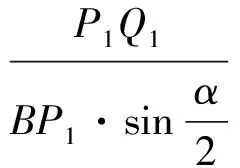
同理可得

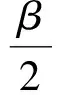
又因为

所以

P1I∥DE.

注意到过点I只能引一条平行于DE的直线，因此点P1与点P重合.又点P在AI上的投影是唯一的，所以点Q1与点Q重合，即点Q在△ABC的外接圆上.