一道2010年清华大学自主招生题的探究

●

(育才中学 上海 201801)

一道2010年清华大学自主招生题的探究

●龚新平

(育才中学 上海 201801)

2010年五校自主招生联考清华大学特色考试试题中出现了如下的离散最值问题(见文献[1]).本文将对该问题提供3种解答,并在此基础上应用逆推法与逐步调整法深入地加以探究,构造提出一个近似估计的求解方案，同时将原问题进行一些变式推广.现笔者将过程整理出来,与读者共同探讨.

问题长度为l(l为整数)的木棒可以锯成长为整数的2段,要求任何时刻所有木棒中的最长者长度严格小于最短者长度的2倍.试问:长度为30的木棒至多可以锯成多少段?

1问题简解

解法1只需罗列出满足条件的所有锯木棒方法,过程如下:

30→15,15

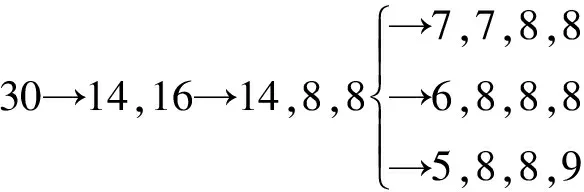
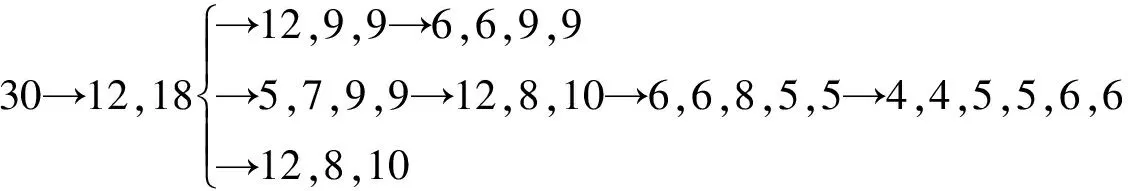
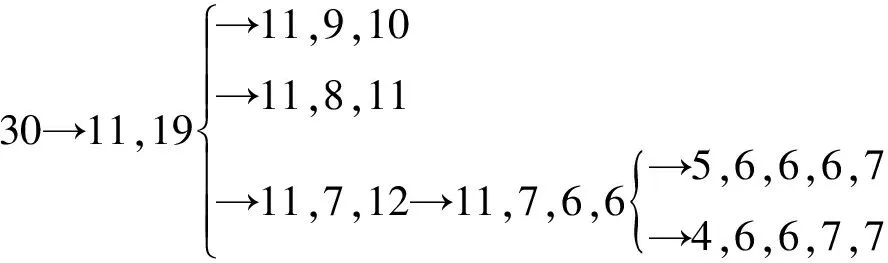
由此可知,长度为30的木棒至多可以锯成6段,具体锯棒过程为:

30→12,18→12,8,10→6,6,8,10→6,6,8,5,5→4,4,5,5,6,6.

解法2最多能锯成6段,构造如下:

30→12,18→12,8,10→6,6,8,10→6,6,8,5,5→4,4,5,5,6,6.

若能锯成7段,设为x1,x2,…,x7,(x1≤x2…≤x7),则显然x7gt;4.若x7≥7,则x1≥4,而4×6+7=31≥30,产生矛盾,故x7=5或x7=6.

当x7=6时,只能是6,4,4,4,4,4,4,逆推得6,8,4,4,4,4,矛盾;

当x7=5时,只能是5,5,4,4,4,4,4或5,5,5,4,4,4,3或5,5,5,5,4,3,3,以上逆推均得出矛盾,故无法锯成7段.从而7段以上也不能锯出!

2初步探究

探究1最小长度至多2段.

若最小长度至少3段,则任两段之和不小于最小长度的2倍,矛盾!

探究2当lgt;2时,最小长度大于1.

若最小长度等于1,由最大长度小于2知,所有长度均为1,而lgt;2,故至少有3个1,矛盾!

探究3非最小长度至多3段.

若某长度至少4段,则一段和比其小的长度由其和长度锯成,剩下该长度的3段中必有2段由其和长度锯成,而此和为第3段的2倍,矛盾!

探究4某长度出现2段后,该长度不能再锯.

若该长度某段再被锯成2段,则其短者之2倍必不大于该长度的另一段,矛盾!

探究5木棒每次被锯时,将长度a锯成b,c(b≥c),则

(1)a是被锯前的最大者;

(2)c是被锯后的最短者.

若存在a′≥a=b+c≥2c,矛盾;若存在c′≤c≤b,则2c′≤c+b=a,矛盾.

3构造探究

由前面的探究,可知欲使定长l锯成最多段数,则小段长度应尽量多。由此得如下构造:

构造1长度为k,k,k+1,k+1,…,2k-1,2k-1或k,k+1,k+1,…,2k-2,2k-2,2k-1,2k-1,2k-1的2k段木棒逆推可合成一根木棒,且满足条件.

证明对k,k,k+1,k+1,…,2k-1,2k-1,由探究5将整个锯棒过程逆推可得:

k,k,k+1,k+1,…,2k-1,2k-1← 2k,k+1,k+1,…,2k-1,2k-1←…←

2k,2k+2,…,4k-2←4k+2,…,

易见以上各步中任何时刻所有木棒最长者均小于最短者长度的2倍.同理可得,对k,k+1,k+1,…,2k-2,2k-2,2k-1,2k-1,2k-1,由探究5将整个锯棒过程逆推可得:

k,k+1,k+1,…,2k-2,2k-2,2k-1,2k-1,2k-1←2k+1,…,←

2k+1,2k+3,…,4k-2←4k+4,….

以上各步任何时刻所有木棒最长者也小于最短者长度的2倍!

探究6最小长度为k时,至多可以锯成的段数n≤2k.

由前面的构造1,可知长度为l的木棒当最小长度为k时,至多可以锯成如下2k段,即

l→k,k,k+1,k+1,…,2k-1,2k-1,

或

l→k,k+1,k+1,…,2k-2,2k-2,2k-1,2k-1,2k-1,

及其各种部分片段,故n≤2k.

构造2木棒长度为l=k(3k-1)+i,对每个i=1,2,3,…,k-1时,均至多可以锯成2k段.

证明对2k段木棒k,k,k+1,k+1,…,2k-1,2k-1中从左至右的偶数位置上(最后一个2k-1除外)的数从左至右依次将一个数加1,或将2个数加1,或将3个数加1,…,或将i个数加1后,得到的长度k,k+1,k+1,k+2,…,k+i-1,k+i,k+i,…,2k-1,2k-1仍满足条件.此时,木棒长度为

l=2[k+(k+1)+…+(2k-1)]+i=k3k-1+i,

即木棒长度l=k(3k-1)+i,(i=1,2,3，…,k-1)时,至多可锯成2k段.

探究7最小长度k应满足3k2-1≥l.

由构造2,易得

l≤2[k+(k+1)+…+(2k-1)]+(k-1)=3k2-1.

同理由构造2,可得

探究8当最小长度为k,木棒长度l=k(3k-1)+i(i=0,1,2,…,k-1)时,至多可锯成2k段.

4问题新解

由前面的探究,可得到原问题的如下解法3:

解法3由最小长度k应满足3k2-1≥30,可得k≥4,而至多可以锯成2k段的木棒最短长度

l=4+4+5+5+6+6+7+7=44.

在此基础上去掉个数最少而和为14的若干段的最佳方案是去掉2个7,于是长度为30的木棒至多可以锯成6段:4，4，5，5，6，6,逆推得具体过程为:

4，4，5，5，6，6←8,5,5,6,6←8,10,6,6←8,10,12←18,12←30.

5变式探究

探究9设木棒长度为l=k(3k-1)-i.

(1)当i=k,k+1,…2k-1时,由于k,k,k+1,k+1,…,2k-1,2k-1中每个数不能减少(否则不符合题意),因此直接去掉一个i,从而至多可以锯成2k-1段;

(2)当i=2k,2k+1,2k+2,…,2(2k-1)时,由于每个i均可表示成k,k,k+1,…,2k-1,2k-1中的2个数之和,因此至多可锯成2k-2段.

变式1长为l(l为整数)的木棒可以锯成长为整数的2段,要求任何时刻所有木棒中的最长者长度严格小于最短者长度的2倍.试问:长度为40的木棒至多可以锯成多少段?

解由最小长度k应满足3k2-1≥40,可得k≥4,而至多可以锯成2k段的木棒最短长度

l=4+4+5+5+6+6+7+7=44.

在此基础上去掉个数最少而剩下数和为40的最佳方案直接去掉一个4,即长为40的木棒至多可以锯成如下7段:4,5,5,6，6，7，7，由逆推可得其具体锯法过程为:

4，5，5，6，6，7，7←9,5,6,6,7,7←9,11,6,7,7←9,11,13,7←16,11,13←16,24←40.

变式2长为l(l为整数)的木棒可以锯成长为整数的2段,要求任何时刻所有木棒中的最长者长度严格小于最短者长度的2倍.试问:长度为18的木棒至多可以锯成多少段?

解由最小长度k应满足3k2-1≥18,可得k≥3,而至多可以锯成2k段的木棒最短长度为

l=3+3+4+4+5+5=24.

在此基础上去掉个数最少而剩下数和为18的最佳方案是去掉2个3或去掉1个3与1个4而将剩下1个4变为5,于是长为18的木棒至多可以锯成4段:4,4,5,5或3,5,5,5,逆推得具体锯法为:

4,4,5,5←8,5,5←8,10←18或3,5,5,5←8,5,5←8,10←18.

对长度为l=k(3k-1)-i(i=1,2,3,4,5,…,k-1)的木棒至多可以锯成多少段的问题,在具体问题中应用逐步调整法总可以得到最佳答案!下面来看具体的变式问题:

变式3长为l(l为整数)的木棒可以锯成长为整数的2段,要求任何时刻所有木棒中的最长者长度严格小于最短者长度的2倍.试问:长度为23的木棒至多可以锯成多少段?

解由最小长度k应满足3k2-1≥23,可得k≥3,而至多可以锯成2k段的木棒最短长度为

l=3+3+4+4+5+5=24.

在此基础上去掉个数最少而剩下数和为23的最佳方案是将其中4个数变为2个而和减少1,于是长为23的木棒至多可以锯成4段:5,5,6,7或4,5,7,7或4,6,6,7,逆推得具体锯法为:

5,5,6,7←10,6,7←10,13←23或4,5,7,7←9,7,7←9,14←23或4,6,6,7←10,6,7←10,13←23.

在前面的变式探究中,当木棒的长度l=3k(3k-1)-i(i=1,2,…,2k-1)时,笔者应用逐步调整法给出了一个较好的求解方法来探求最佳答案.除此之外,是否还有更直接而简洁的方法呢?期待与大家共同探讨!

[1] 范端喜.名牌大学自主招生高效备考[M].上海:华东师范大学出版社，2010.