三角形等角线的一个新性质及应用

●

(开化县第二中学 浙江开化 324300)

三角形等角线的一个新性质及应用

●曹嘉兴

(开化县第二中学 浙江开化 324300)

如图1，自△ABC的顶点A引2条射线AX，AY，分别交对边BC于点X，Y，并使AX，AY关于∠BAC的平分线AD对称，那么线段AX，AY就叫做△ABC的等角线(因为AX，AY与∠BAC的2边分别构成相等的角，故有这个名称).文献[1]给出了三角形等角线的一些基本性质，本文将给出三角形等角线的一个新的基本性质.

定理1自△ABC的顶点A引2条等角线AD，AE，分别交对边BC于点D，E,则

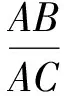
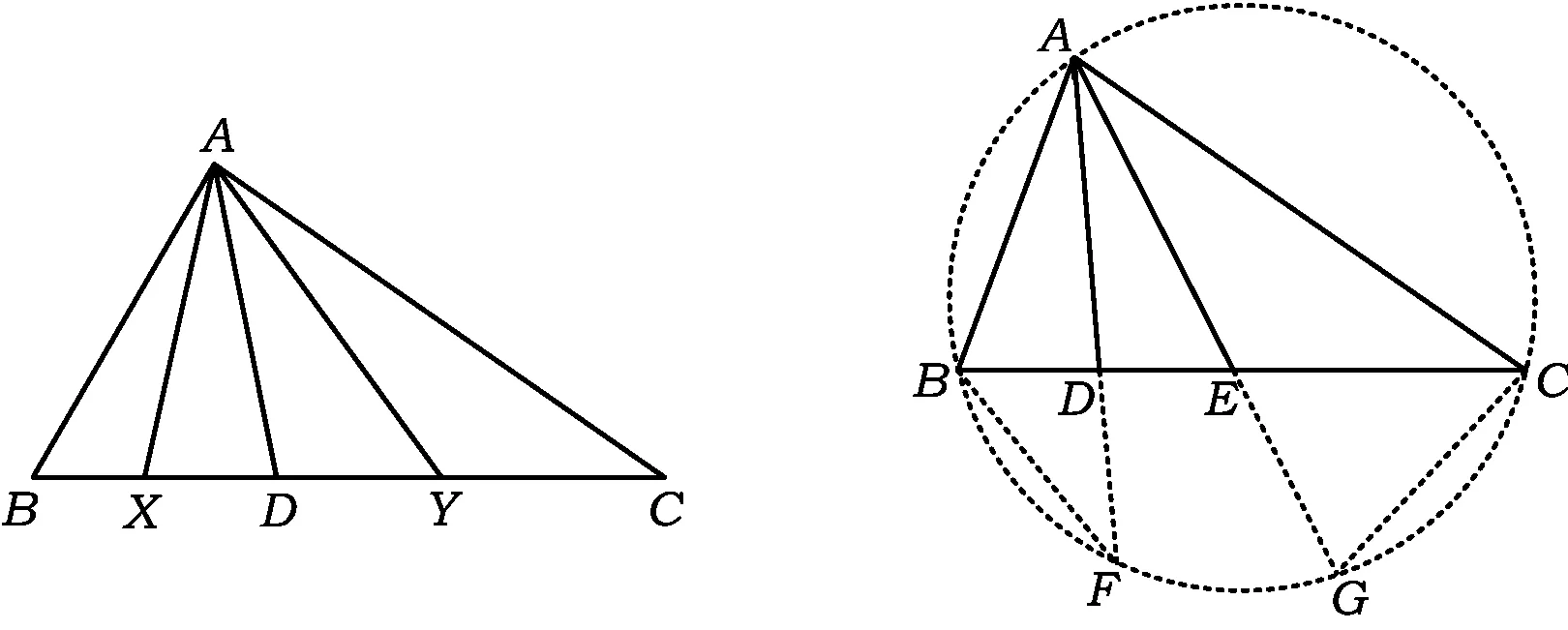
图1 图2

证明如图2，作△ABC的外接圆，设AD，AE的延长线与△ABC的外接圆分别交于点F，G，连结BF，CG.由∠BAD=∠CAE,∠ABC=∠AGC得

△ABD∽△AGC,

(1)

又由∠BAD=∠CAE,∠ACB=∠AFB得

△ACE∽△AFB,

(2)

式(1)×式(2),并利用BF=CG得

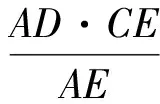
(3)

又由△ABD∽△AGC得

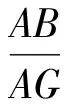
于是AB·AC=AD·AG=AD(AE+EG)=

AD·AE+AD·EG.

(4)

由相交弦定理得

AE·EG=BE·CE，

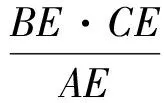
(5)

又由式(3)，式(4)，式(5)得

AB·AC=AD·AE+AD·EG=

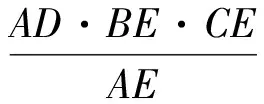
同理可证,定理1的第2式也成立.

该定理的2个结论结构对称,形式优美，易于记忆，利用它来解决某些平面几何问题甚为方便、简捷，请看以下几例．

图3

例1自△ABC的顶点A作射线AX，AY分别交对边BC于点X，Y，使∠BAX=∠CAY,求证:

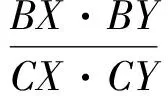
(1986年上海市初中数学竞赛试题)

证明如图3，由本文定理1的2个结论得

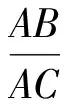
因此

即

例2自△ABC的顶点A引2条等角线AD，AE,交对边BC分别于点D，E，则

BD·BE·CD·CE=(AB·AC-AD·AE)2.

证明由定理1的2个结论得

(6)

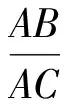
(7)

式(6)×式(7)得

BD·BE·CD·CE=(AB·AC-AD·AE)2.

注上面的2个例题分别是文献[1]给出的三角形等角线的2个基本性质,利用定理1的2个结论可以轻松地证明这2个基本性质.

例3在△ABC中,M为BC边上的任一点,ME⊥AB于点E,MF⊥AC于点F,AN⊥EF交BC于点N,求证:

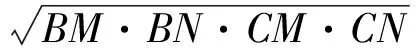
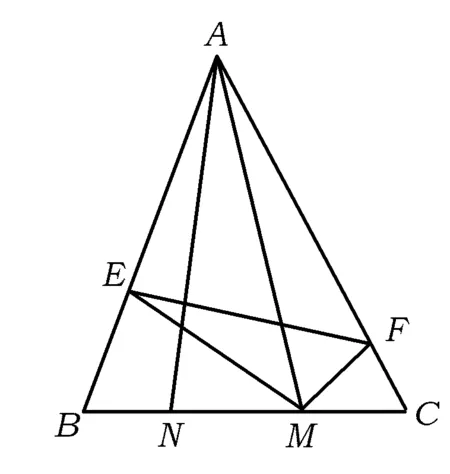
图4

证明如图4,因为ME⊥AB,MF⊥AC,所以A，E，M，F四点共圆,因此

∠MEF=∠CAM.

又因为AN⊥EF,所以∠BAN与∠AEF互余.又∠MEF与∠AEF互余,从而∠BAN=∠MEF,于是∠BAN=∠CAM,因此AM，AN是△ABC的2条等角线.

由定理1的2个结论得

(8)

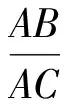
(9)

式(8)×式(9)得

(AB·AC-AM·AN)2=BM·BN·CM·CN,

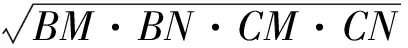
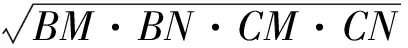
例4在△ABC中,AD是∠BAC的平分线,则

AD2=AB·AC-BD·DC.

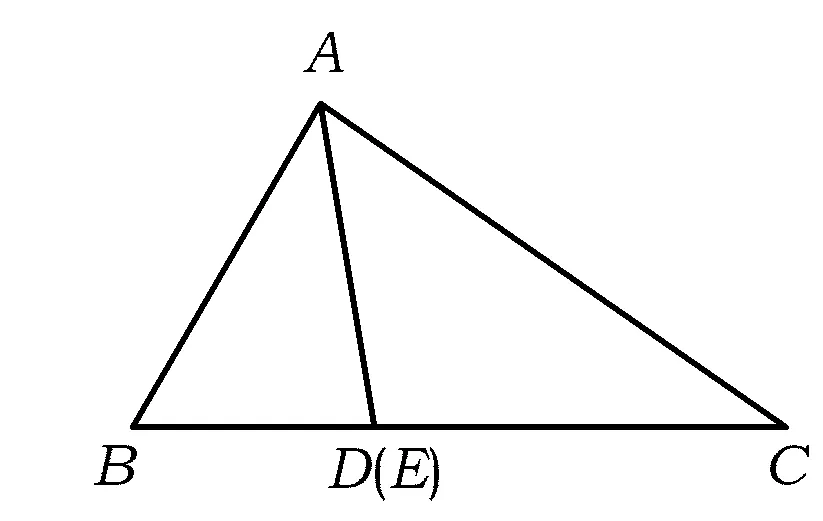
图5

证明当图2中的2条等角线AD，AE互相重合时便得到AD平分∠BAC(如图5),此时由本文定理1中的第1个结论可得

又由角平分线的性质定理得

把式(11)代入式(10)得

即

AD2=AB·AC-BD·DC.

注由此可见著名的Schooten定理(F.Van.Schooten,约1615-1660年,荷兰数学家)是本文定理的特例,因此定理1也可以看作是Schooten定理的一种推广.

[1] 李耀文.三角形等角线的性质初探[J].中学教研(数学),2001(7):23-27.

[2] 沈康身.历史数学名题赏析[M].上海：上海教育出版社，2010:466.