滚动轴承故障监测诊断中的自适应滤波算法
席玉洁,马波,冯坤
(北京化工大学 诊断与自愈工程研究中心,北京 100029)
常规的轴承故障诊断中,伴随着设备工况的变化,载波的频带会发生变化,需要人为提前确定载波频率的特征带,而这些参数的选择取决于操作者的经验或历史数据,经过反复的试验才能确定,给实际应用带来了很多不便。因此设计简便、有效的滤波过程十分重要。近年来有些学者尝试使用先进的时频分析方法来自动进行轴承的故障诊断。文献[1-2]将谱峭度方法规范化,并且提出了谱峭度的快速算法——峭度图,并将该方法应用于故障诊断中取得了较好的效果。但该方法采用的滤波器较为单一,变化有限,难以准确地匹配故障特征。文献[3]利用连续复Morlet小波变换的优势,在全频带范围内对信号进行包络分析,自动设定滤波中心频率,由于Morlet小波波形参数是确定的,使得小波与冲击成分的匹配程度大大降低,影响了包络效果。文献[4]提出了一种基于连续小波变换和谱峭度分析的改进包络方法,并将其应用于轴承的故障检测中,取得了一定效果,但没有介绍如何确定带通滤波器的带宽。文献[5]指出小波分析进行特征提取容易丢失原始信号局部信息,不能有效地去除原始信号的噪声,且提升小波的方法只能根据信号的特点设计预测滤波器系数,而做不到更新滤波器系数。因此,在此提出基于峭度指标的自适应最优滤波算法。
1 基本理论
1.1 共振解调法
共振解调法又称包络分析法,是目前轴承故障诊断中最常用的方法之一。其利用轴承或检测系统作为谐振体,把故障冲击产生的高频共振响应放大,通过包络检测方法将其变为具有故障特征信息的低频波形,对包络信号进行频谱分析便可容易地诊断出轴承的故障[6]。轴承故障分析信号处理诊断技术路线如图1所示[7]。

图1 轴承故障分析诊断技术路线
1.2 峭度系数
峭度系数K是反映振动信号分布特性的数值统计量,是归一化的4阶中心矩,
(1)

对于一组给定的离散振动信号数据,其峭度系数K为
(2)
峭度系数表示故障形成的大幅值脉冲出现的概率,对时域信号变换的陡峭程度非常敏感,在轴承故障诊断中具有实际意义。
峭度指标是无量纲参数,由于与轴承转速、尺寸、载荷等无关,对冲击信号特别敏感,特别适用于表面损伤类故障(尤其是早期故障)的诊断。在轴承无故障运转时,由于各种不确定因素的影响,振动信号的幅值分布接近正态分布,峭度指标值K≈3;随着故障的出现和发展,振动信号中大幅值的概率密度增加,信号幅值的分布偏离正态分布,正态曲线出现偏斜或分散,峭度值也随之增大。峭度指标的绝对值越大,说明轴承越偏离其正常状态,故障越严重。如当K>8时,则很可能出现了较大的故障[8]。文献[9]指出时域参数中峭度作为诊断轴承的指标效果较好。
2 最优滤波算法
根据峭度系数的实际意义对滤波过程进行了改进设计。设计流程如图2所示。
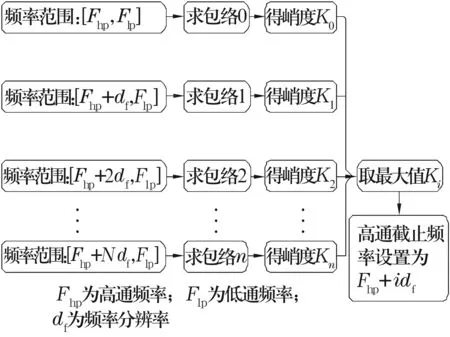
图2 自适应最优滤波算法设计流程图
自适应最优滤波算法的实现主要包括以下几个步骤:
(1)为了防止频谱混叠引起的信号失真,设定抗混滤波线(即流程图中的低通截止频率,根据经验一般定为采样频率的1/3),对原始信号进行抗混滤波;
(2)设定初始高通滤波频率,在高通滤波频率和抗混滤波频率范围内,以一个频域分辨率(图2中df)为步长依次选取一系列频率,作为试探截止频率;
(3)以选取的每个试探截止频率对信号进行带通滤波,然后对每一组数据进行包络,求出多组包络波形;
(4)计算每一组包络波形对应的峭度系数,得到多个峭度值;
(5)通过比较找出最大的峭度值,取峭度最大时的截止频率作为最优滤波算法的高通截止频率,对应的那组波形作为最优的包络波形;
(6)对最优包络结果进行频谱分析,分析故障频率,进行轴承故障的诊断。
3 试验数据分析
3.1 试验条件
对型号为N205有外圈故障的圆柱滚子轴承进行测试分析。轴承安装在试验台上,外圈固定,内圈由转轴带动,转速无级可调,以1 700 r/min的转速回转。振动信号由压电加速度传感器从轴承座上采集,通过电荷放大器放大后经采样记录到计算机。试验台设置如图3所示。

图3 试验台装置图
试验中所使用的N205轴承的参数为:Dw=6.477 mm,Dpw=38.481 mm,Z=13,α=0°。可计算出轴承外圈故障的特征频率为153.168 Hz。
3.2 试验方案及数据分析
取采样频率20 kHz,采样点数80 000;由试验装置加速度传感器采得的原始信号如图4所示。

图4 原始信号波形
对于图4所示的轴承外圈故障的时域信号,峭度值为3.613 4,该峭度指标值已经说明轴承有早期的故障,但从图4中观察不到任何由故障所产生的周期性脉冲振动成分,因此,不能判断故障类型。
3.3 与固定频率滤波的比较
图5为信号经固定频率滤波(固定滤波频率6 000 Hz)后做出的功率谱,显然在此功率谱中并不能清楚地观察到故障特征频率,因此也不能对故障的类型进行判断。

图5 固定频率滤波功率谱
如图6所示,在用自适应最优滤波的方式求得的功率谱上,在信号的高频区域可清楚地看到由轴承故障所引起的周期性脉冲成分。通过计算,可以得知滤波截止频率为6 725 Hz时求出的峭度值最大(K=15.161 0),表明在6 725 Hz处进行滤波效果最好。因此由该处滤波所对应的包络便可以选作最佳包络。

图6 自适应最优滤波功率谱
图6中可以清楚地观察到轴承外圈的故障特征频率153 Hz,且其2次、3次等谐波非常明显,由此可得出该轴承有外圈故障的诊断结论。比较图5与图6可以得出以下结论:(1)由自适应最优滤波方法做出的功率谱可以清楚看到由轴承缺陷所产生的冲击振动成分,而固定滤波后做出的功率谱无法判断;(2)图6中得到轴承的故障频率为153 Hz,与计算结果吻合。
3.4 与小波包变换的比较
使用文献[10]中小波包变换的方法对试验中的轴承进行故障诊断。利用小波包算法对图4中的信号进行分析,结果如图7所示。

图7 小波包滤波算法的功率谱
从图7的功率谱分析中可以看出,由小波包变换选择滤波频段并进行滤波后,得到的功率谱有许多杂波,不容易诊断出轴承发生的为何种故障。而自适应最优滤波算法得到了很好的效果。这是由于小波包变换本质上是对信号进行等带宽多带滤波,可能导致许多有用的信息被滤除,不能反映真实的故障信息;此外,带宽大小及最优小波包基的选择准则的不同,也可能给诊断带来误差。
4 结束语
分析结果表明,此算法用于滚动轴承故障诊断,保证了故障诊断结果的准确性,实现了自动更新滤波器系数,使诊断过程对人的经验和历史数据的依赖降到了最低,在实际工程应用中有很大优势。

