基于模糊控制零电流钳位逆变器死区补偿
刘栋良 武瑞斌 张 遥 王家军
(杭州电子科技大学自动化学院 杭州 310018)
1 引言
逆变器作为交流调速驱动的核心,逆变器性能的好坏直接决定了系统的控制性能和节能的效率。一般功率器件的导通时间小于关断时间,如果不设置一定的触发延迟,将导致上下功率器件的直通,这个设定的触发延迟也就是逆变器的死区时间。在逆变器存在的地方就存在逆变器死区效应的影响,死区的存在将导致交流伺服系统存在如下的问题:
(1)逆变器的输出电压发生畸变,使得电动机的端电压与逆变器的参考电压存在偏差,降低了伺服控制的精度。
(2)导致零电流的钳位现象,从而电动机的输出转矩发生脉动,特别是在电动机运行于低速时影响更加严重,甚至导致系统的不稳定。
Ueda R[1]等人首先针对感应电动机提出了逆变器死区的存在可能会导致系统的不稳定,对于死区造成的不稳定性进行了理论分析。Ueda R[2]等人又针对不同的感应电动机给出了在不同逆变器死区情况下的实验结果。Dodson R[3]等人研究了逆变器死区对于输出电压的影响,死区的存在能够使得输出电压的基波降低5%~15%,同时还会使逆变器的输出电流包含大量的谐波,加重了系统对电网的谐波污染,降低了整个控制系统的效率。Murai Y[4]、Choi J[5]等人分析了如果在死区开始逆变器的输出电流很小(接近于零)时,将出现零电流钳位现象。当前对于逆变器死区的研究主要集中于电压前馈和电流反馈补偿。Jeong S[7]等人通过分析逆变器的参考电压和输出电压的误差,根据死区时间和直流母线电压进行补偿,这种方法简单易行,但由于没有对功率器件的导通压降进行补偿而存在补偿误差。Choi J[8]等人引入死区补偿时间来补偿死区效应,由于死区补偿时间未知,并且随工作点的不同而发生变化,因此需要在线辨识,固定的死区补偿有时会使得补偿误差加大。Urasaki N[9]和Kim H[10]等人基于永磁同步电动机交流伺服系统采用干扰观测器的方法对逆变器的死区效应进行在线补偿,该方法把逆变器死区和开关器件的非理想特性所造成的转子交直轴电压作为干扰电压进行在线估计,然后反馈到逆变器参考电压进行电压前馈补偿,该方法由于干扰观测器的设置,补偿电压存在相位滞后,同时对干扰观测器增益的选择需要一定的经验。Murai Y[4]等人采用裂分零电压矢量的方法来解决逆变器死区所导致的零电流钳位问题,然而死区对电压的影响仍然需要补偿。Choi J[5]等人兼顾电压的补偿和消除零电流钳位问题,由于补偿电压是和工作点有关,所以通过电压平均来补偿误差电压消除零电流钳位现象存在补偿误差。Summers T[11]等人采用预测电流控制来降低逆变器死区所导致的零点电流钳位问题,然而系统为局部稳定系统。
综上所述,考虑到开关器件固有特性和死区效应的复杂性,用传统的方法来实现精确的死区补偿不够理想。本文提出了一种新型的模糊补偿算法,该算法能够对永磁同步电动机伺服系统提供精确的零电流信息,可以实时计算逆变器死区导致的误差电压,并通过前馈方式对误差电压进行补偿,有效地消除零电流钳位现象。最后,仿真与实验表明了系统设计是有效性和可行性。
2 零电流钳位分析
逆变器和永磁同步电动机的结构如图1所示。为了防止直流母线电压短路,必须在同一桥臂的功率器件导通之前加入一定的触发死区。如图所示,在关断S1,开通S2之间增加一段时间(死区时间),在死区时间内,当 a相电流较大且ia>0时,逆变器桥臂 a相中的 S1关断,同时 S2没有开通,则电流只能通过VD2二极管来续流,a相电压在死区时间内钳位于-Vdc/2;相反,在死区时间内,当a相电流较大且ia<0时S2关断时,同时S1没有开通,则电流只能通过VD1二极管续流,a相电压在整个死区时间内钳位于Vdc/2,整个过程如图2所示。在图2中,由上到下五组曲线分别表示:实际参考电压,同一桥臂的上、下两个功率器件的触发信号,逆变器实际输出电压,输出电压和实际参考电压的误差。由图2可以得出如下的结论:
(1)死区造成误差电压和输出电流的方向相反。
(2)死区造成的误差电压宽度为死区时间,在一个电流周期内的脉冲电压的个数为载波比。
(3)脉冲电压的高度为直流母线电压。
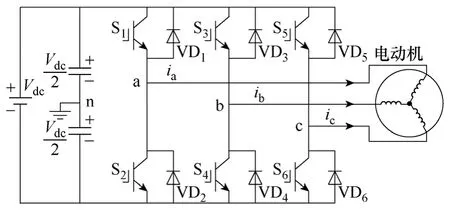
图1 逆变器和电动机结构Fig.1 Inverter and motor structure
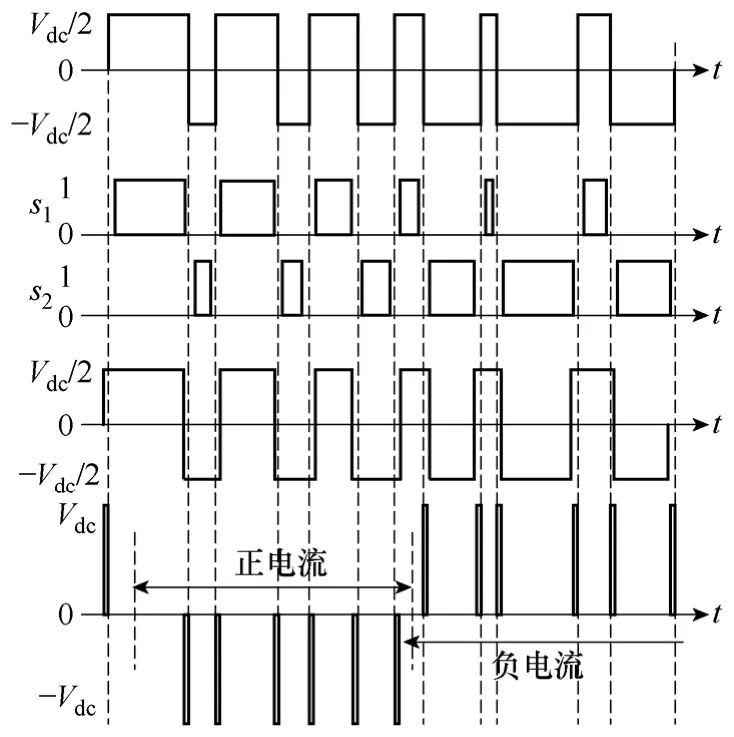
图2 逆变器死区对于输出电压的影响Fig.2 Effects of inverter dead time on output voltage
当前大部分逆变器死区的补偿都是以上面的分析为原则[4-6],并且假定在死区期间电流的方向不变。Murai Y[1]、Choi J[2]等人分析了如果在死区开始,逆变器的输出电流很小时,逆变器的输出电流将在整个死区时间内钳制在零点附近,电动机在运行于低速并且电动机的电流很小时,电流钳位现象会更加明显,这将大大的增加了死区对输出电压和电流的畸变影响,导致电动机输出转矩的波动,甚至导致系统的不稳定。因此,如果在零电流钳位期间仅根据电流来判断电流方向补偿死区电压误差是不精确的,甚至会起到相反的作用。
图3给出了一个永磁同步电动机伺服系统的零电流钳位仿真示意图。由图3可以得出如下的结论:
(1)逆变器死区的零电流钳位发生在电流过零附近,在整个死区期间电流被钳位于零附近。
(2)电流在过零之前的一段时间内受到死区的影响很小,在电流过零以后的一段时间内被钳位于零附近。
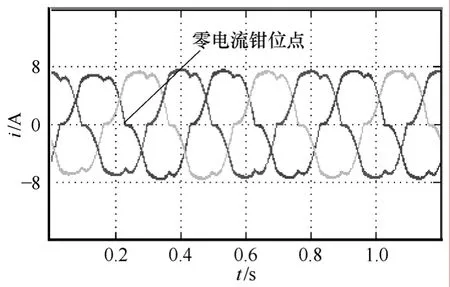
图3 零电流钳位图Fig.3 Zero current clamping
3 模糊控制补偿设计
3.1 模糊控制设计
零电流钳位时电压补偿关键是对零电流附近电流方向的判断。由图 3可以得出电流过零的特征。图4a给出了负电流过零的特征图,图4b给出了正电流过零的特征图。根据图 4,可以利用电流的导数di和电流i,根据模糊控制方法判断电流的方向dout。

图4 电流过零分析Fig.4 Current cross zero analysis
di和i的模糊语言变量为{NB,NS,Z,PS,PB}。
dout的模糊语言变量为{N,Z,P}。
模糊规则如下:
规则 1:IFi为 NS AND di为 NS则 dout为 N;
规则 2:IFi为 NS AND di为 PB则 dout为 N;
规则 3:IFi为 PS AND di为 NB则 dout为 P;
规则 4:IFi为 PS AND di为 PS则 dout为 P;
规则 5:IFi为NB则dout为N;
规则 6:IFi为PB则 dout为P;
规则 7:IFi为 Z AND di为 NB则 dout为 P;
规则 8:IFi为Z AND di为PB则 dout为N;
规则 9:IFi为 Z AND di为 Z则 dout为 Z。
根据以上的模糊控制算法,在零电流钳位时可以得到正确的电流方向。
3.2 电压补偿计算[13]
当ia为正方向时,逆变器死区所导致的开通时间误差和电压误差为

当ia为负方向时,逆变器死区所导致的开通时间误差和电压误差为
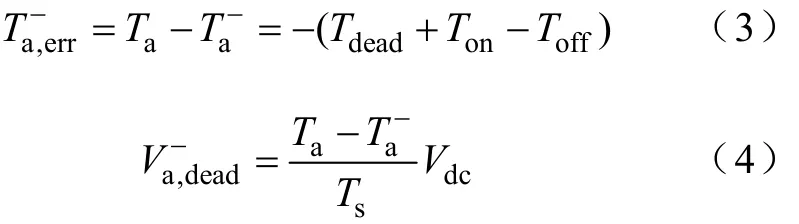
由式(1)、式(2)、式(3)和式(4)得 a相死区补偿电压
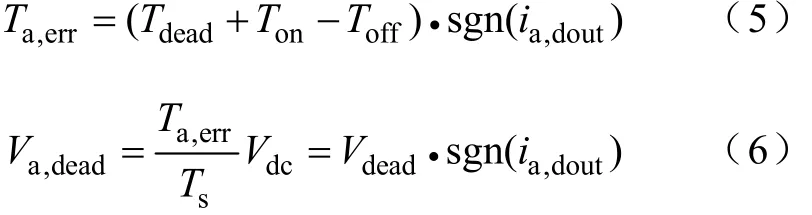
式中,ia,dout为由模糊控制得到的a相电流大小,
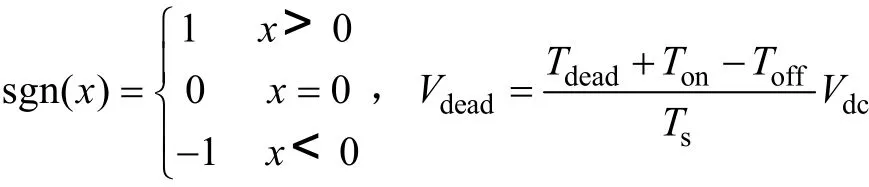
同样也可以得到b,c两相的死区补偿电压
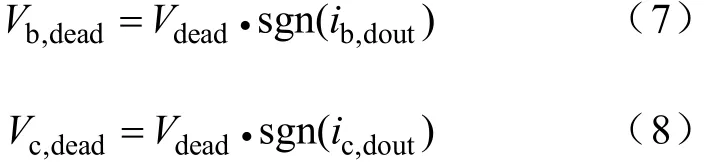
将 a,b,c三相死区补偿电压,转换到基于转子的dq坐标为
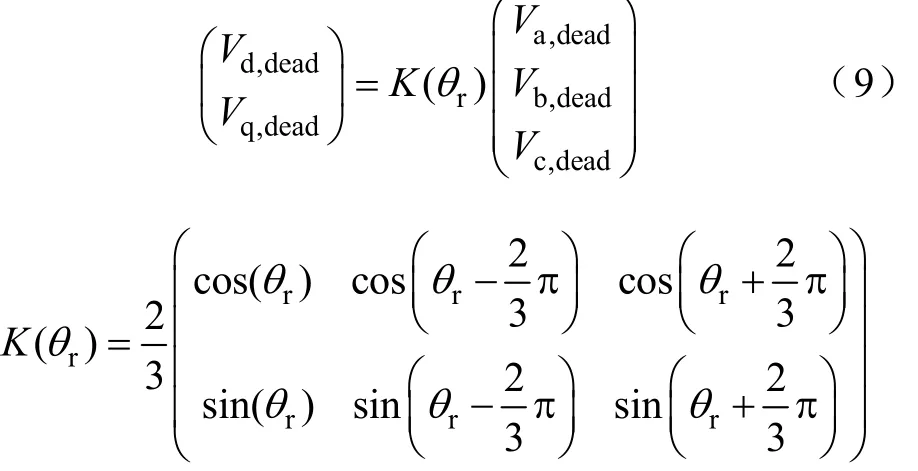
式中,θr为转子角位置。
4 仿真分析
永磁同步电动机伺服系统的模糊控制结构框图如图5所示。仿真电动机参数:额定功率2kW,额定转速2000r/min,极对数为4,定子相电阻0.43Ω,额定转矩9.55N·m,电感0.20mH,转子转动惯量为 42.6kg·cm2;智能功率模块为 PM50RLB060;IGBT 的参数为ton=1.0μs,toff=1.2μs,开关频率为20kHz,输入工作电压为AC220V,设定死区时间为tdead=2.13μs。给定负载转矩分别为0N·m,5N·m。通过Matlab仿真(转速15r/min):在没有逆变器死区补偿的情况下的电流仿真波形如图6所示,在算法补偿情况下的电流仿真波形如图7所示。由仿真结果可以看出,在没有补偿时零电流钳位导致输出转矩的脉动,并且在逆变器穿越零点后更加严重。通过算法补偿可以及时地补偿逆变器死区所导致的误差电压,有效地消除零电流钳位现象,降低转矩的脉动。

图5 系统控制框图Fig.5 Control figure of system
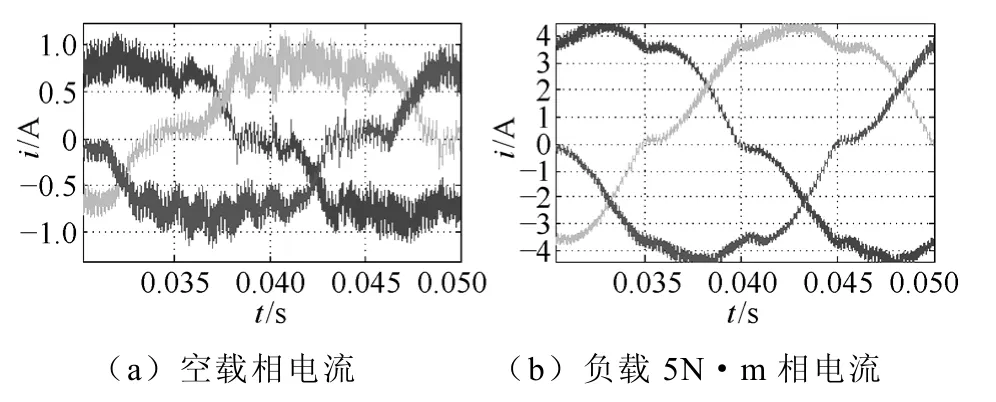
图6 无补偿情况仿真波形Fig.6 Curve of no compensation
图7 补偿情况仿真波形Fig.7 Curve of compensation
5 实验验证
整个控制系统以TI公司的TMS320F2810 DSP芯片为核心,以三菱智能IPM为驱动模块组成的伺服系统。实验条件:转速15r/min时,采用Agilent(DSO6014A)示波器,检测相电流如图 8所示,其中图 8a为空载条件下电流波形,图 8b为负载5N·m时的电流波形,从图中可以看出电流存在严重的钳位现象,且转矩脉动比较大;通过模糊补偿算法,相电流波形,如图9所示。电流波形的平滑性、正弦性均明显优于补偿前的电流波形。同时,从图8b、图9b可以看出,由于负载的加大,增加了给定电压值,使电压畸变减小,从而降低死区效应对电动机低速运行时电流波形的影响。
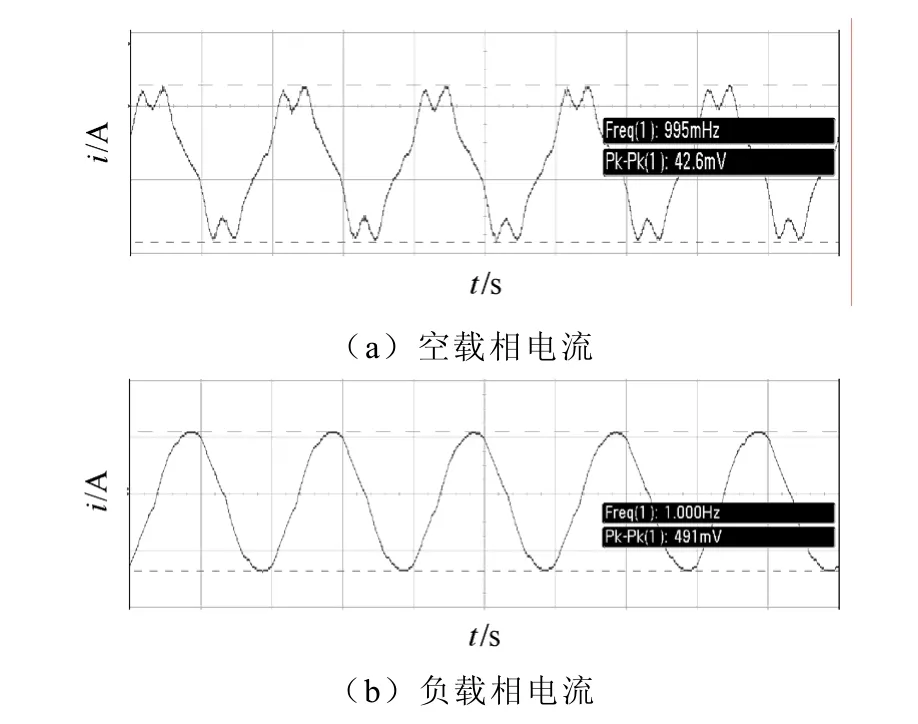
图8 无补偿情况下相电流波形Fig.8 Current waveforms on no compensation

图9 死区补偿情况下相电流波形Fig.9 Current waveforms on dead-time compensation
6 结论
逆变器死区导致的零电流钳位现象,从而使电动机输出转矩产生脉动,降低了伺服系统的控制精度,采用模糊控制方法能够精确估计钳位电流的方向,并且实时计算逆变器死区补偿电压。该设计方法能够有效消除逆变器死区导致的零电流钳位现象,提高死区的补偿效率,降低低频时输出电流波动,从而提高伺服低速性能,保证精度。
[1] Ueda R, Sonoda T, Inoue Y. Unstable oscillating motor in PWM variable speed drive of induction mode and its stabilization[C]. Records of Industry Applications Society Annual Meeting, San Francisco,USA, 1982.
[2] Ueda R, Sonoda T, Takata S. Experimental results and their simplified analysis on instability problem in PWM inverter induction motor drives[J]. IEEE Transactions on Industrial Applications, 1989, 25(1):86-95.
[3] Dodson R, Evans P. Compensating for dead time degradation of PWM inverter waveforms[J]. IEE Proceedings B: Electric Power Applications, 1990,137(2): 73-81.
[4] Murai Y, Riyanto A, Nakamura H, et al. PWM strategy for high frequency carrier inverters eliminating current clamps during switching dead-time[C]. Records of Industry Applications Society Annual Meeting, Houston, TX, 1992:317-322.
[5] Choi J, Sul S. New dead time compensation eliminating zero current clamping in voltage-fed PWM inverter[C]. Records of Industry Applications Society Annual Meeting, USA, 1994.
[6] 王家军, 许镇琳, 王豪, 等. 基于逆变器死区特性的永磁同步电动机系统的μ-修整变结构控制[J]. 中国电机工程学报, 2003, 23(4): 148-152.
Wang Jiajun, Xu Zhenlin, Wang Hao, et al.μ-modification variable structure control of PMSM system based on inverter dead-time[J]. Proceedings of the CSEE, 2003, 23(4): 148-152.
[7] Jeong S, Park M. The analysis and compensation of dead-time effects in PWM inverters[J]. IEEE Transactions on Industrial Electronics, 1991, 38(2):108-114.
[8] Choi J, Sul S. Inverter output voltage synthesis using novel dead time compensation[J]. IEEE Transactions on Power Electronics, 1996, 11(2): 221-227.
[9] Urasaki N, Senjyu T, Uezato K. On-line dead-time compensation method for permanent magnet synchronous motor[C]. IEEE International Conference on Industrial Technology, Bangkok, 2002, 1: 268-273.
[10] Kim H, Moon H, Youn M. On-line dead-time compensation method using disturbance observer[J].IEEE Transactions on Power Electronics, 2003, 18(6):1336-1345.
[11] Summers T, Betz R. Dead-time issues in predictive current control[C]. Records of Industry Applications Society Annual Meeting, Pittsburgh, USA, 2002.
[12] Kim K H, Youn M J. A simple and robust digital control technique of a PM synchronous motor using time delay control approach[J]. IEEE Transactions on Power Electronics, 2001, 16(1): 72-82.
[13] 刘栋良, 贺益康, 交流伺服系统逆变器死区效应分析与补偿新方法[J]. 中国电机工程学报, 2008,28(21): 46-50.
Liu Dongliang, He Yikang. Analysis and compensation of AC servo system on inverter dead-time effect[J].Proceeding of the CSEE, 2008, 28(21): 46-50.
[14] 程小猛, 陆海峰, 瞿文龙, 等. 用于逆变器死区补偿的空间矢量脉宽调制策略[J]. 清华大学学报,2008, 48(7): 1077-1080.
Cheng Xiaomeng, Lu Haifeng, Qu Wenglong, et al.SVPWM strategy for inverter dead-time compensation[J].Tsinghua University: Science & Technology, 2008,48(7): 1077-1080.
[15] 吴茂刚, 赵荣祥, 汤新舟. 矢量控制永磁同步电动机低速轻载运行的研究[J]. 电工技术学报, 2005,20(7): 87-92.
Wu Maogang, Zhao Rongxiang, Tang XinZhou. Study of vector-controlled PMSM at low speed and light load[J]. Transactions of China Electrotechnical Society,2005, 20(7): 87-92.
[16] 贾红云, 程明, 花为, 等. 基于死区补偿的磁通切换永磁电机定子磁场定向控制[J]. 电工技术学报,2010, 25(11): 48-55.
Jia Hongyun Cheng Ming Hua Wei, et al. Statorflux-oriented control for flux-switching permanent magnet motor based on dead-Time compensation[J].Transactions of China Electrotechnical Society, 2010,25(11): 48-55.
[17] 王高林, 于泳, 杨荣峰, 等. 感应电机空间矢量PWM 控制逆变器死区效应补偿[J]. 中国电机工程学报, 2008, 28(15): 79-83.
Wang Gaolin, Yu Yong, Yang Rongfeng, et al. Dead time compensation of space vector PWM inverter for induction motor[J]. Proceedings of the CSEE, 2008,28(15): 79-83.
[18] 孙向东, 钟彦儒. 一种新颖的死区补偿时间测量方法[J]. 中国电机工程学报, 2003, 23(2): 103-107.
Sun Xiangdong, Zhong Yanru. A novel measuring method for dead-time compensation[J]. Proceedings of the CSEE, 2003, 23(2): 103-107.
[19] 毛鸿, 吴兆麟. 基于三相 PWM 整流器的无死区空间矢量调制策略[J]. 中国电机工程学报, 2001,21(11): 100-104.
Mao Hong, Wu Zhaolin. The no dead-time space vector modulation strategy based on three-phase PWM rectifiers[J]. Proceedings of the CSEE, 2001,21(11): 100-104.

