基于电磁斥力原理的高速触头机构仿真分析与设计
江壮贤 庄劲武 王 晨 刘路辉 戴 超
(海军工程大学电气与信息工程学院 武汉 430033)
1 引言
由高速机械触头与功率半导体并联组成的混合型限流断路器具有通流容量大、关断速度快、限流能力强等优点,是新型限流断路器发展的一个主要方向[1]。在混合型限流断路器中为了限制、分断高上升率短路电流,要求它必须具备高反应速度及动作速度,能够在短路故障发生初期切断故障电路。由于功率半导体器件的动作速度极快,因而机械触头机构的反应速度成为制约限流断路器性能发挥的瓶颈。同时限流断路器在切断短路电流时触头两端会出现远大于系统电压的瞬时过压,因此要求机械触头能够获得尽量大的初始速度,尽早形成绝缘间隙。
基于电磁感应涡流原理的电磁斥力机构具有机械延迟时间短,初始运动速度快的优点[2-7],特别适合用于驱动机械触头高速分闸,已被广泛应用于混合式直流限流断路器[8]、真空直流断路器[9]、新型超导限流器[10]等电力系统的限流保护设备的高速触头驱动机构中。
文献[11]运用电路理论和传输线理论推导出使电磁斥力机构效率最大化的运动部件特征质量的计算方程,并通过仿真分析指出实际工程上可实现的斥力机构能达到的最大效率约为30%,但该文只分析了运动部件质量对斥力机构效率的影响,无法全面反应斥力机构其它参数对斥力影响的规律,不能用于指导实际机构的设计。文献[12]采用仿真方法对应用于真空触头驱动系统的电磁斥力机构进行参数分析,得到了设计的一般性原则,但其分析的重点在于如何缩短行程时间。实际上限流型断路器更关注机械触头在接到分断信号后的反应速度以及初期的运动速度。文献[13]采用基于平行排列的同轴双圆形线圈模型,导出了计算电磁推力的基本分析公式,分析了电磁推力机构的工作性能与结构参数的一般关系,但并没有具体研究其电磁学与机械动力学特性,距离实现机构的优化设计尚远。
本文采用有限元仿真方法对电磁斥力机构进行建模分析。通过对改变电磁斥力机构结构及电气参数得到的不同仿真结果进行分析,得到了这些参数对电磁斥力机构动作效果影响的规律,并以此为指导设计了基于电磁斥力机构的高速机械触头。研制了基于电磁斥力原理的高速触头机构样机,该样机的初始分离时间为 220μs,试验结果与仿真算例的比较,证明了仿真分析的正确性。
2 电磁斥力机构的工作原理

图1 电磁斥力机构工作原理Fig.1 Working principle of electro-magnetic mechanism
电磁斥力机构一般由脉冲放电回路、斥力线圈和斥力金属盘三部分组成,如图1所示。其中脉冲电容C,功率晶闸管VT、续流二极管VD和斥力线圈组成了机构的脉冲放电回路。当晶闸管接到触发信号导通后,预先储能的电容对斥力线圈放电形成脉冲电流,该电流在斥力线圈周围产生脉冲磁场,位于斥力线圈正上方的斥力金属盘由于脉冲磁场的作用形成感应涡流,且方向与斥力线圈中的电流方向相反,因而感应涡流所产生的磁场与线圈产生的磁场方向相反,从而在斥力线圈与斥力金属盘间产生巨大的电磁斥力,推动运动部件高速运动。
3 电磁斥力机构数学模型
斥力机构动作时,根据能量守恒定律电源提供的能量dAs应等于机构所做的dA功与磁场中能量的变化dw以及热损耗dQ之和,即

如果斥力线圈与斥力盘之间有磁耦合,可以写出它们的能量平衡关系式为

式中,e1与e2、i1与i2、R1与R2分别为斥力线圈与金属盘的电压、电流和电阻。
两个线圈的磁能w决定于下式
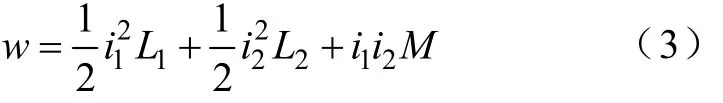
式中L1——斥力线圈的电感;
L2——斥力盘电感;
M——互感。
联立式(1)~式(3)可得机构所做的功为

由于L1、L2都为常数,则机构的电磁斥力为

从式(5)可见,电磁斥力F与斥力线圈电流i1、斥力金属盘上的感应电流i2及线圈与铜盘间的互感对斥力金属盘位移的导数dM/(dz)成正比。
4 电磁斥力机构有限元仿真模型
为了研究电磁斥力机构的动态特性,本文采用电磁场有限元仿真软件Ansoft对电磁斥力机构进行建模。由于电磁斥力机构为轴对称结构,可以采用Ansoft的RZ二维平面来建立等效模型,图2所示为进行有限元剖分后电磁斥力机构的二维轴对称模型。网格分得越多计算结果越准确,但是计算量也越大。
在加入边界条件时除了常规的气球边界外,需要把线圈看作是一个低阻值的电感,其外部电路如图3所示。其中L与R为线圈自身的电阻和电感,C为预先充电的电容,VD为续流二极管,Lcircuit为线路电感。用电流探头表笔监测线圈电流。

图2 电磁斥力机构的有限元网格划分Fig.2 Finite elements of the mechanism

图3 边界条件中的外部电路Fig.3 External circuit in simulation
5 电磁斥力机构参数仿真分析
5.1 斥力线圈匝数分析
改变斥力线圈匝数得到的仿真结果如图 4a所示,当线圈的匝数为20匝时,斥力峰值为21kN,而当线圈匝数为10匝和40匝时,斥力峰值分别为13kN和 17.5kN。斥力线圈的电感与电阻与线圈匝数密切相关。当线圈匝数较少时,电感与电阻较小,因而脉冲电流峰值较大,但由于线圈匝数少使得磁通变化率小,因而斥力峰值较小;当线圈匝数达到一定程度后,再增加线圈匝数会使线圈的电感和电阻过大而导致脉冲电流过小,因而斥力又随着匝数的增加而减小。同时斥力线圈匝数越多,斥力峰值时间越迟,导致运动部件加速的时间过长,不能在短时间内达到最大值。因而在机构设计时应选择合适的斥力线圈匝数,使电磁斥力能够在短时间内达到最佳值,从几种仿真算例的结果来看,线圈匝数为20时,机构作用效果最好。
5.2 斥力铜盘厚度分析
图 4b所示为斥力铜盘厚度分别为 0.5mm、2mm、4mm和6mm四种情况时电磁斥力的曲线。当铜盘厚度为 0.5mm时,电磁斥力峰值最小为16kN;当铜盘厚度为 2mm时,电磁斥力峰值增加为19kN;当铜盘厚度为4mm和6mm时斥力峰值大小基本上一致,为21kN。依据电磁场理论,当高频电流在导体中流过时由于趋肤效应电流将集中在导体表面。电磁斥力机构的脉冲磁场在斥力盘中感应的涡流由于趋肤效应,大部分分布在2倍趋肤效应的渗透深度2d以内,其中

式中ω——信号角频率;
μ——材料的磁导率;
σ——材料的电导率。
在所设计电磁斥力机构样机中及放电电路中ω=1.57×104rad/s,μ≈μ0=4π×10–7H/m,σ=5.8×107S/m。代入式(6)可得该条件下斥力盘的趋肤深度为1.2mm。由于斥力盘感应的涡流绝大部分集中在 2倍趋肤深度2.4mm之内,当斥力盘厚度大于2.4mm后继续增加厚度不能明显增加斥力峰值,相反会由于运动部件质量的增加使触头加速度变小。因此在机构设计时,从斥力角度考虑只需使斥力盘厚度等于2倍趋肤深度即可,但是为了保证一定的机械强度使斥力盘在巨大电磁斥力的作用下不发生塑性形变则应当增加斥力盘的厚度或在斥力盘上方增加其他高强度的支撑。
5.3 斥力盘与斥力线圈间隙分析
改变斥力盘与斥力线圈的初始间隙 gap,得到的仿真结果如图4c所示。间隙越小,线圈与斥力盘耦合越好,斥力越大;气隙越大,线圈的等效电感越大,斥力线圈中的脉冲电流上升率越小,因而斥力越小,斥力峰值时间越长。当斥力间隙为0.5mm时,电磁斥力峰值可达23kN;而当斥力间隙为4mm时,电磁斥力峰值仅为11.5kN。斥力机构设计时,在条件允许的情况下应使斥力盘与斥力线圈的初始间隙尽量小。
5.4 放电电容容量及充电电压对斥力的影响分析
由于电容储存的能量与电容充电电压的平方及电容容量成正比,因而电容容量或是电容充电电压的提高都会使斥力峰值增大,如图4d、4e所示。但是增大电容容量会使放电周期变长,从而使电磁斥力到达峰值的时间变长,而电容电压的提高则会增加对机构绝缘强度的要求,因此在设计时应根据实际需要选择合适的电容容量及充电电压参数。
5.5 放电线路电感对斥力影响分析
在电磁斥力机构的动作过程中由于斥力盘与斥力线圈的耦合作用使得斥力线圈的等效电感远小于斥力线圈自身的电感,因而线路电感对斥力作用的影响效果明显。改变放电线路电感,保持斥力机构其他参数不变得到的结果如图4f所示。线路电感增大不仅会使斥力峰值减小,而且使峰值时间延迟,不利于运动部件在运动初期获得大的加速度,当线路电感由 1μH 增加到 9μH 时,电磁斥力峰值由24.5kN减小到14kN,斥力峰值时间由90μs增加至150μs。因而在设计时应尽量减小线路电感,若引线过长时应尽量使用双绞线。

图4 电磁斥力机构参数仿真分析Fig.4 Simulation analysis of the mechanism
6 混合型限流断路器高速触头机构
6.1 高速触头机构组成
通过以上对电磁斥力机构各主要参数进行仿真分析,得到了各参数对电磁斥力机构作用效果影响的规律,以此为指导设计了混合型限流断路器的高速触头机构样机如图5所示。该样机由斥力铜盘、斥力线圈、动触头、静触头、连杆、弹簧系统及永磁锁扣机构组成。斥力铜盘位于动触头上方,斥力线圈固定于支架上,合闸时弹簧为触头提供预紧力,此时铜盘正好位于斥力线圈正上方,两者间隙应尽量小,样机参数见下表。

图5 高速触头机构样机Fig.5 Construction of electro-magnetic mechanism

表 电磁斥力机构原理样机参数Tab. Parameters of the mechanism
6.2 高速触头机构试验分析
通过外部充电电路将斥力电容充至工作电压,触发放电回路晶闸管使放电回路导通,用电流传感器测量斥力线圈电流,用直线位移传感器测量各时刻对应的位移,实验得到的结果与仿真计算结果进行对比,如图6所示。图6a为放电脉冲电流波形,电流峰值为5kA,峰值时间100μs。图6b为动触头的位移时间特性曲线,动触头在斥力机构动作的前期便获得了巨大的加速度,推动触头高速运动,斥力作用结束之后,动触头已获得一定的初速度,该速度使触头能够克服弹簧的弹力继续向上运动,并最终由锁扣机构固定于分闸位置。试验结果与仿真计算结果基本吻合,证明了仿真分析的正确性。

图6 样机仿真与实验结果Fig.6 Results comparison between test and simulation
为了测量动、静触头的初始分离时间,在触头两端串联直流电源及5kΩ电阻,触头在合闸状态时电阻两端电压为电源电压,当动静触头分离时电阻两端电压为零,用示波器监测高速触头机构分闸动作时电阻两端电压,如图7所示。在晶闸管触发信号发出220μs后,电阻两端电压跃变为0V,动静触头开始分离。

图7 动静触头分离时间Fig.7 Contact separation time
从样机实验结果可知,所研制高速触头机构动、静触头的初始分离时间为 220μs,从后期对混合型限流断路器的短路分断实验结果证明,该高速触头机构可以满足混合型限流断路器在分断大电流高上升率短路电流时对机械触头机构快速动作、高速分离特性的要求。
假定短路电流上升率为20A/μs,采用高速触头机构,从检测到短路故障到触头分离,功率半导体开始对短路电流进行关断,电流共上升了 4.4kA,而采用传统断路器,其动作时间按3ms计算,在动作过程中电流共上升了60kA。由此可见,对于大容量、高上升率的电力系统采用高速触头机构可极大提高断路器的短路保护能力。
7 结论
本文推导了电磁斥力机构斥力的计算公式,该公式表明电磁斥力与斥力线圈电流、斥力金属盘上的感应电流及线圈与斥力盘的互感对斥力金属盘位移的导数成正比。
采用有限元仿真软件对电磁斥力机构进行仿真分析,得到以下结论:
(1)电磁斥力峰值随着斥力线圈匝数的增加的变化律是斥力峰值先增大后减小,存在一个极大值,而斥力峰值时间随着线圈匝数增加而变长。
(2)电磁斥力峰值随斥力盘厚度的增大先是明显增大,当斥力盘厚度大于2倍趋肤深度之后,斥力盘厚度增加,斥力峰值基本保持不变。
(3)电磁斥力峰值与线圈同斥力盘间的间隙成反比例关系,间隙越大,线圈等效电感越大,斥力峰值越小。
(4)电磁斥力峰值与电容充电电压的平方、电容容量成正比例关系,斥力峰值时间随电容容量的增加而变长。
(5)电磁斥力峰值随线路电感的增加而减小,峰值时间随线路电感的增加而变长。
设计了混合型限流断路器的高速机械触头机构,实验结果证明了仿真分析的正确性。该样机的初始分离时间为 220μs,能够满足混合性限流断路器在大电流条件下限制、分断高上升率短路电流的要求。
[1] Yu Kimori K, Kenichi K, Hiroyu Ki S, et al. Development of the high speed switch and its application[C].Conference Record of IAS Annual Meeting (IEEE Industry Applications Society), 1998: 2321-2328
[2] Sayed A H E, Ker Kenaar R W P, Atmadji A M S.Modeling the opening mode of a fast acting electrodynamic circuit-breaker drive[C]. Proceedings of the Universities Power Engineering Conference, Leicester,UK, 1999: 169-173.
[3] Ahn K Y, Kim S H. Modeling and analysis of a high-speed circuit breaker mechanism with a springactuated cam[J]. Proceedings of the Institute of Mechanical Engineers, 2001, Part C: 663-672.
[4] 娄杰, 李庆民, 孙庆森, 等. 快速电磁推力机构的动态特性仿真与优化设计[J]. 中国电机工程学报,2005, 25(8): 23-29.
Lou Jie, Li Qingmin, Sun Qingsen, et al. Dynamic characteristics simulation and optimal design of the fast electromagnetic repulsion mechanism[J]. Proceedings of the CSEE, 2005, 25(6): 23-29.
[5] Genji T, Nakamura O, Isozaki M, et al. 400V class high-speed current limiting circuit breaker for electric power system[J]. IEEE Trans. on Power System, 1994,9(3): 1428-1435.
[6] Hui D, Wang Z K, Zhang J Y, et al. Development and test of 10.5 kV/1.5kA HTS fault current limiter[J].IEEE Trans. on Applied Superconductivity, 2006, 16(2):687-690.
[7] Coquery G, Lallemand R, Josse G, et al. Current limiter device for railway and distribution network design and tests on railway conditions: 1000A-25kV-50Hz[C].EPE 2005, 2005: 1-7.
[8] 王晨, 张晓锋, 庄劲武, 等. 新型混合式限流断路器设计及其可靠性分析[J]. 电力系统自动化, 2008,32(12): 61-67.
Wang Chen, Zhang Xiaofeng, Zhuang Jinwu, et al.Design and reliability analysis of a novel hybrid current-limiting circuit breaker[J]. Automation of Electric Power Systems, 2008, 32(12): 61-67.
[9] Alferov D, Budovaky D, Evsin V, et al. DC vacuum circuit-breaker[C]. Proceedings of the 23rd International Symposium on Discharges and Electrical Insulation in Vacuum, 2008, 1 and 2: 173-176.
[10] Jadidian J. A compact design for high voltage direct current circuit breaker[J]. IEEE Transactions on Plasma Science, 37(6): 1084-1091.
[11] Sadedin D R. A study of the magnetic inductionrepulsion accelerator[C]. Proceedings of the 8th IEEE International Pulsed Power Conference Digest of Technical Papers 1991: 68-72.
[12] 王子建, 何俊佳, 尹小根, 等. 基于电磁斥力机构的 10kV快速真空开关[J]. 电工技术学报, 2009,24(11): 68-75.
Wang Zijian, He Junjia, Yin Xiaogen, et al. 10kV high speed vacuum switch with electromagnetic repulsion mechanism[J]. Transactions of China Electrotechnical Society, 2009, 24(11): 68-75
[13] 李庆民, 刘卫东, 钱家骊, 等. 电磁推力机构的一种分析方法[J]. 电工技术学报, 2004, 19(2): 20-24.
Li Qingmin, Liu Weidong, Qian Jiali, et al. An analytical method for electromagnetic repulsion mechanism[J]. Transactions of China Electrotechnical Society, 2004, 19(2): 20-24.

