基于LCL滤波的大功率三相电压型PWM整流器

李欣然 郭希铮 王德伟 郝瑞祥 游小杰

（北京交通大学电气工程学院 北京 100044）

1 引言

三相电压型 PWM整流器具有直流电压可控、网侧输入电流畸变率低、功率因数高以及能量可以双向流动等优点，广泛应用于工业系统和新能源并网发电系统中[1-3]。但是采用PWM调制方法导致电网电流中含有开关频率附近的高频谐波，干扰电网中的EMI敏感设备。传统的三相电压型PWM整流器交流侧采用L滤波。在大功率应用场合中，开关频率较低，为了将谐波电流限制在相关标准允许的范围内，需要较大的电感量，这会使得系统的动态响应变慢，电感的体积增大，成本增加。目前，采用LCL滤波器代替L滤波器是解决这个问题的有效方法[4-7]。由于电容对高频谐波的滤波作用，达到相同滤波效果时，LCL滤波器的总电感量远小于L滤波器的电感量，因此LCL滤波器适合应用于中、大功率场合。

本文首先分析了采用LCL滤波器时三相电压型PWM 整流器系统数学模型及控制算法，然后根据IEEE-519标准[8]要求的电流谐波限制条件，利用SVPWM调制方式产生谐波电压幅值进行迭代运算来计算LCL滤波器参数，同时从离散域分析了采用无源阻尼（passive damping）时系统的稳定性。在此基础上，本文研制了一台 500kW 三相电压型PWM 整流器样机，对系统关键部分构成进行了分析，实验结果验证了上述分析方法的有效性。

2 三相电压型PWM整流器控制算法

三相电压型PWM整流器主电路如图1所示。网侧采用LCL滤波器取代传统L滤波器。图中，Lg为网侧电感，Lr为变流器侧电感，Rg和Rr分别为网侧电感和变流器侧电感等效电阻，Cf为滤波电容，Rd为阻尼电阻，Cd为直流支撑电容，esk为电网相电压，igk为网侧电流，irk为变流器侧电流，urk为变流器侧相电压，Udc为中间直流电压，idc为直流负载电流。其中下标k=a,b,c。

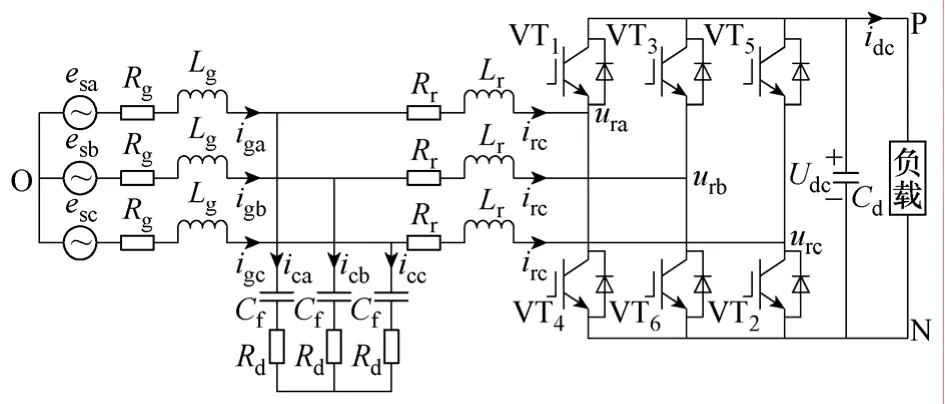
图1 基于LCL滤波的三相电压型PWM整流器主电路Fig.1 Main circuit of three-phase voltage source PWM rectifier with LCL filter

PWM整流器采用LCL滤波时，滤波电容支路主要通过高次谐波电流，因此低频时忽略滤波电容Cf的影响，可将 LCL滤波器建模为 L滤波器：L=Lg+Lr，R=Rg+Rr。基于LCL滤波器的PWM整流器在dq同步旋转坐标系下的数学模型为

由此得到电网电压定向时系统的控制方程为

根据式（2），采用电压、电流双闭环控制方法，控制算法框图如图2所示。

根据电网电压定向的原理，d轴和q轴分别控制有功功率和无功功率分量，直流侧电压PI输出为d轴电流指令，控制系统有功电流，以达到控制直流侧电压的目的。

当q轴电流指令值为0时，系统为单位功率因数控制。当直流侧空载、q轴电流指令不为 0时，系统运行于无功补偿工况。

当q轴电流指令符号为正时，系统发出感性无功，相当于三相电容器。q轴电流指令符号为负时，系统发出容性无功，相当于三相电抗器。假设系统三相平衡，控制算法中采用等幅坐标变换，q轴电流指令值为，电网相电压有效值为Es，则系统发出的无功功率Q为

图2 电网电压定向控制算法框图Fig.2 Block diagram of the grid-voltage oriented control algorithm

3 LCL滤波器参数设计

3.1 参数设计

LCL滤波器的参数设计相对较复杂，设计不合理时不仅达不到预期滤波效果，反而会增加电流畸变，造成系统性能恶化。

近年来，很多学者对LCL滤波器的设计方法进行研究。Marco Liserre对LCL滤波器参数的限制条件及设计步骤做了介绍[4]。文献[5]利用谐振频率作为中间参数，通过推导电流谐波衰减比例的二次方程得到设计结果。文献[6]指出 LCL参数设计与开关频率密切相关，但上述方法对该点并未进行详尽说明。文献[7]设定网侧谐波电流衰减比例系数，根据SVPWM的各次谐波电压设计LCL滤波器参数，但该系数选取对参数设计的影响并未分析。

本文采用的LCL滤波器设计方法，考虑了文献[4]提出的滤波器参数设计的限制条件，将谐振频率、网侧电感与整流器侧电感的比例因子作为已知量，利用 SVPWM 调制方式时的电压谐波值，根据IEEE-519标准要求的电流谐波限制条件，迭代计算LCL滤波器参数。该设计方法易于实现，计算次数较少，所得参数准确可靠。

假设三相平衡，整流器交流侧输出等效为受控电压源并忽略电感等效电阻时，系统单相等效电路如图3a所示。图3b为系统单相等效谐波模型，将整流器交流侧输出等效为谐波电压源，并假设电网为理想电压源，谐波电压为零。本文所提出的设计方法均基于该模型。

图3 LCL滤波器单相等效电路Fig.3 Single-phase equivalent circuit of LCL filter

系统空载时，其交流侧的基波电压有效值Ur1,0与电网相电压有效值Es相等，采用SVPWM调制方式时，其空载调制比M0为

当系统满载时（额定电流），交流侧的基波电压有效值Ur1,n为

式中，Ig1,n为整流器相电流额定值，定义网侧、变流器侧电感比例因子r=Lg/Lr，即Lg=rLr，根据LCL滤波器谐振频率fres定义k1=fres/f1，其中谐振频率为

那么额定功率下，SVPWM满载时调制比Mn为

根据LCL参数可以计算各谐波电流分量如下：

在LCL滤波器参数未知时，无法计算满功率条件下SVPWM调制比，因此，采用一种迭代算法，将r、fres作为输入变量，首先根据空载调制比M0计算（mf-2）次电压谐波，由式（9）～式（11）分别计算LCL滤波器参数Cf、Lr、Lg。

式（10）中，Igh,max为满足IEEE-519标准计算得到的第h次谐波最大电流有效值。将计算得到的参数代入式（7）计算额定功率下调制比Mn，进而计算Urh,n，根据式（8）计算Igh,n，若

表明参数满足设计要求，若不满足式（12），修改Igh,max，重新进行计算，算法流程图如图4所示。

图4 LCL滤波器参数设计流程图Fig.4 Flow chart for design method of LCL filter

本文采用双重傅里叶级数的方法计算 SVPWM的谐波[9]，根据上述迭代算法得到的LCL滤波器参数为：Lg=130μH,Lr=250μH,Cf=600μF。

500kW PWM整流器样机参数见下表。

表 500kW PWM整流器样机参数Tab. Parameters of the 500kW PWM rectifier

3.2 LCL采用PD时离散域稳定性分析

由图3b可得LCL滤波器传递函数为

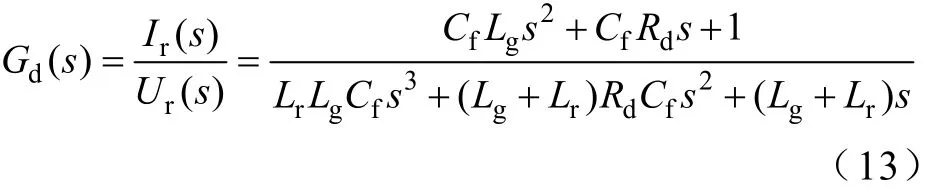
LCL滤波器的谐振特性可由其频率响应曲线说明，如图5所示，当无阻尼电阻（Rd=0）时，LCL滤波器在703Hz附近发生谐振，随着阻尼电阻的增大，谐振点响应幅值不断减小。可以看到，LCL滤波器具有谐振特性，因此无阻尼或欠阻尼可能造成系统不稳定。

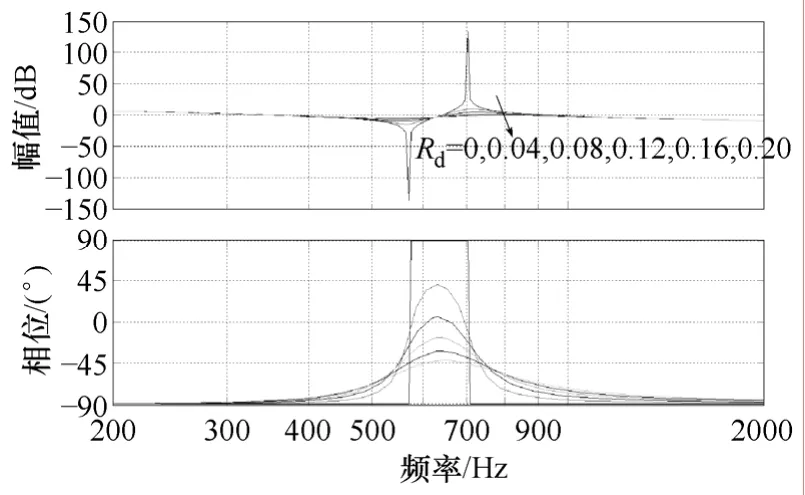
图5 不同阻尼电阻值时LCL滤波器伯德图Fig.5 Bode plot of LCL filter with varying damping resistance

图6 离散域电流环控制框图Fig.6 Block diagram of the current loop in discrete domain

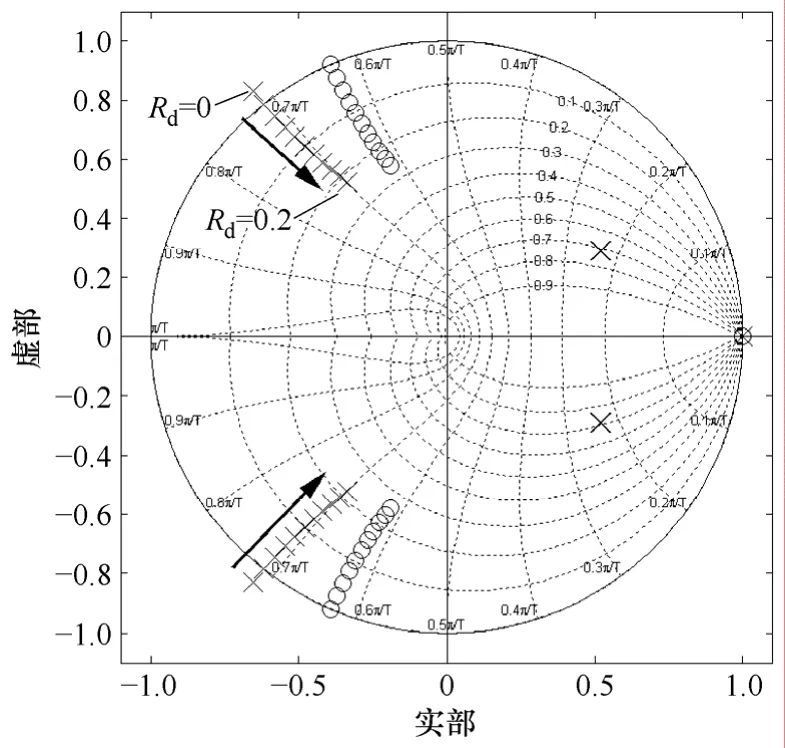
图7 采用无源阻尼时电流环离散域传递函数零极点分布Fig.7 Pole-zero map of the current loop transfer function with PD in discrete domain

4 系统构成与实验结果分析

4.1 系统构成

在上述分析基础上制造了一台500kW样机，系统框图如图8所示，样机实物如图9所示。

图8 500kW样机系统框图Fig.8 Block diagram of 500kW prototype system

图9 500kW样机Fig.9 Prototype of 500kW PWM rectifier

功率单元中开关器件选用Infineon公司的6单元 IGBT模块 FS450R17KE4。其参数为：耐压值1 700V，峰值电流450A，结温可达到175℃。功率单元设计时，将 1个 FS450R17KE4模块的三个桥臂的上管并联、下管并联构成三相整流器中的一个桥臂，保证额定工况下还留有1倍的电流裕量。

驱动电路选用 Concept公司最新的驱动器2SC0650P，它具备双通道驱动能力，能工作在1 700V电压下，开关频率最高可达150kHz，每个通道驱动功率6W，驱动电流可达±50A，满足了功率单元中一个桥臂上、下两组开关器件（6支IGBT）所需的驱动能力要求，并且其具有短路、过电流以及欠电压保护功能。

控制系统电路分为DSP主控板、AD采样板、IO板、光纤接口板和电源板。核心处理器选用 TI公司的TMS320F28335浮点型DSP，它的主频可达150MHz，具备丰富的外设，适合电机和变流器控制。AD采样芯片选用TI公司的ADS8364，16位精度，6通道同时采样。

4.2 实验结果分析

系统动态性能验证：直流电压指令值1 100V，空载起动时直流电压波形和网侧电流波形如图10a所示。直流侧由250kW电阻负载突增到500kW电阻负载时，直流电压和网侧电流波形如图10b所示。由动态实验波形可见，空载起动时电压超调不超过5%，突加50%负载时，电压跌落不超过10%，满足实际应用要求。

系统稳态性能验证：额定工况下，系统网侧电流、变流器侧电流和电容支路电流波形（由上到下）如图10c所示。经功率分析仪测定，网侧电流THD为 3.01%，网侧电流和变流器侧电流各次谐波所占比重如图11所示，从图11可以明显看出电流高频谐波得到了有效抑制。

图10 LCL滤波的500kW PWM整流器实验结果Fig.10 Experimental results of 500kW PWM rectifier with LCL filter

图11 额定功率时网侧和变流器侧电流频谱Fig.11 Harmonic spectra of grid side current and converter side current at rated condition

5 结论

本文分析了基于LCL滤波的三相电压型PWM整流器的数学模型及控制算法，提出了利用SVPWM 调制方式产生谐波电压幅值进行迭代运算来设计LCL滤波器参数的方法，然后从离散域分析了采用无源阻尼时系统的稳定性。在此基础上，本文研制了一台 500kW 三相电压型 PWM整流器样机，实验结果验证了上述分析方法的有效性。

[1] 苑国锋, 李永东, 柴建云, 等. 1.5MW 变速恒频双馈风力发电机组励磁控制系统试验研究[J]. 电工技术学报, 2009, 24(2): 42-47.

Yuan G F, Li Y D, Chai J Y, et al. Experimental investigation on excitation control system of 1.5mw variable speed constant frequency DFIG wind generator system[J]. Transactions of China Electrotechnical Society, 2009, 24(2): 42-47.

[2] 赵争鸣, 刘建政, 等. 太阳能光伏发电及其应用[M].北京: 科学出版社, 2005.

[3] Kazmierkowski M P, Krishnan R, Blaabjerg F.Control in power electronics: selected problems[M].USA: Academic Press, 2002.

[4] Liserre M, Blaabjerg F, Hansen S. Design and control of an LCL-filter-based three-phase active rectifier[J].IEEE Transactions on Industry Applications, 2005,41(5): 1281-1291.

[5] 张宪平, 李亚西, 等. 三相电压型整流器的 LCL滤波器分析与设计[J]. 电气应用, 2007, 26(5): 65-68.

Zhang X P, Li Y X, et al. Analysis and design of LCL type filter for three-phase voltage source rectifier[J].Electrotechnical Application, 2007, 26(5): 65-68.

[6] Kamran Jalili, Steffen Bernet. Design of LCL filters of active-front-end two-level voltage-source converters[J].IEEE Transactions on Industrial Electronics, 2009,56(5): 1674-1689.

[7] Chen Y, Jin X M. Modeling and control of three-phase voltage source PWM rectifier[C].CES/IEEE 5th International Power Electronics and Motion Control Conference, 2006, 3: 1459-1462.

[8] IEEE Standard 519-1992. IEEE Recommended Practices and Requirements for Harmonic Control in Electric Power Systems[S].

[9] Moynihan J F, Egan M G, et al. Theoretical spectra of space-vector-modulated waveforms[J]. IEE Proceedings Electric. Power Applicatios, 1998,145(1): 17-24.

[10] Liserre M, Dell’Aquila A, Blaabjerg F. Stability improvements of an LCL-filter based three-phase active rectifier[C]. Power Electronics Specialists Conference, 2002, 3: 1195-1201.