小型直流电磁继电器温度场仿真分析

苏秀苹 陆俭国 刘帼巾 常 伟

（河北工业大学电器研究所 天津 300130）

1 引言

随着低压电器的发展，继电器的应用越来越广泛，对继电器的要求也越来越高。传统的设计模式费用高，周期长。电器稳定工作时的温升是电器设计生产中的一个重要参数，直接影响着电器的稳定性和寿命。文献[1]应用有限元分析软件ANSYS对直流接触器中电磁铁的温升情况进行了分析，而没有对整体进行分析。文献[2]对交流接触器工作时的发热情况做了分析。文献[3]应用有限元方法对密封电磁继电器进行了分析。文献[4]描述了断路器的热分析。本文分析的小型直流电磁汽车继电器工作环境比较恶劣，负荷电流也相对较大。文中对汽车继电器在不同线圈电压下的生热、散热情况做了分析，得到稳态时的温度场分布，并将线圈平均温升与实验数据进行了比较。

2 分析模型

因为研究对象为非对称结构，所以对继电器整体进行建模，建立的实体模型去掉外壳后的结构如图1所示。

图1 直流继电器模型Fig.1 DC relay simulation model

对触头接触部分的建模使用了一小圆柱体来模拟触点球面处的接触电阻。圆柱的截面半径和高度计算如下。

触头收缩电阻为[5]

式中ρ——材料的电阻率；

a——触头接触面半径。

则触头接触面半径，即小圆柱体的截面半径为

且

式中A——接触面面积，A=πa2。且

建模时采用动合触头闭合时两引出脚之间电阻实测值，约为2.3mΩ。

3 分析计算

继电器在达到热稳定后，其发热功率与散热功率相同。下面分别从发热和散热两方面对继电器的稳态温升进行分析。

3.1 发热分析

直流继电器工作时的热源包括线圈和动静触头导电回路两部分。

3.1.1线圈发热功率的计算

线圈的发热功率可用下式表示

式中U——线圈电压；

Rx——线圈电阻。

线圈电阻随铜导线电阻率变化而变化，而铜导线电阻率的数值是随温度变化的[6]

式中ρ0——0℃时的电阻率，ρ0=1.62×10-8Ω·m；

θ——温度；

α——电阻温度系数。

在分析过程中，温度是变化的，所以在分析中考虑了电阻率随温度的变化。当温度为 0～180℃时，电阻率的取值范围为 1.62×10-8～2.87×10-8Ω·m。

在 ANSYS热分析中，发热功率是通过单位体积的生热率进行加载的。则对线圈施加载荷为

式中qx——线圈单位体积的生热率；

Vx——线圈体积。

当对线圈加载热载荷时，考虑了线圈电阻随温度的变化。

3.1.2线圈温升的计算

在试验测试中，线圈温升的计算采用的是电阻测量法，所以所得的线圈温升是一个平均值。

因为分析时，计算的是节点和单元温度，所以线圈的平均温升值可由单元的温升值得到

式中Tk——线圈模型中的单元k的温度；

Vk——单元k的体积；

T0——环境温度。

3.1.3动静触头导电回路发热功率计算

动静触头导电回路的发热功率为

式中I——触头导电回路加载电流；

Rcont——触头导电回路电阻。

触头导电回路采用了耦合场分析方法。在ANSYS耦合场分析中有两种不同的分析方法：顺序耦合和直接耦合。本文采用了直接耦合的方法，使用了226实体单元，在分析中同时考虑了热和电的材料属性。

触头导电回路加载20A电流。动静触头引出脚的端部表面各自耦合节点电压，其中一个引出脚端部表面的电压为0，另一个引出脚端部加载电流。

3.2 散热分析

继电器的散热主要有三种途径：内部传导散热外部辐射和对流散热。

3.2.1内部传导散热

继电器内部散热的主要方式是传导散热。稳态时继电器内部的传导散热为[6]

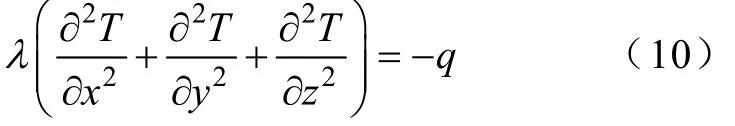
式中T——物体的温度；

λ——导热系数，其值随温度变化；

q——单位体积内热源的生热率。

3.2.2表面的散热分析处理

表面的散热是通过对流散热和辐射散热共同作用完成的。

（1）对流散热遵循下式[6]

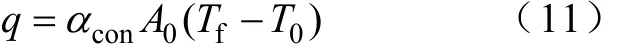
式中q——热流量，W；

αcon——对流散热系数，W/(m2·℃)；

A0——对流散热面积，m2；

Tf——发热体温度，℃；

T0——环境温度，℃。

边界的对流散热系数与周围流体的特性有关，此处取经验公式[6]

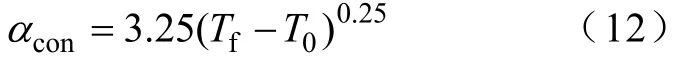
（2）辐射散热：依据 Stefan-Boltzmann定律,物体的辐射散热为

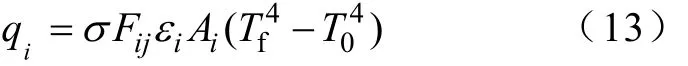
式中qi——热流量；

Fij——形状系数，在计算外壳和导线外表面辐射散热时取Fij=1；

εi——发射率，此处参考外壳黑色塑料的发射率[7]，取εi=0.92；

σ——Stefan-Boltzmann常数，σ=5.67×10-8W/ (m2·K4)。

（3）触头引出脚处外接导线的当量折合。此处需要说明的是在对试品进行分析时，因为接触回路部位要通过20A的电流，且引出脚的导热性能很好，所以引出脚的整体温升都较高，此时需要考虑触头导电回路外接导线对散热的影响。在建模时曾在带外壳的试品中加上外接导线（据标准要求，导线长度取0.1m）研究连接导线对线圈温升的影响。后考虑到模型尺寸协调和简化问题，将外接导线对线圈温度的影响折合到引出脚的端部，即外接导线的影响通过接线端的边界条件来代替，计算结果表明此种折合对温升误差影响不大。处理方法如下：

导线中通过电流，因此产生焦耳热，自身温度升高。同时外接导线处于空气中，主要通过对流和辐射散热。裸导线的对流散热系数为[8]

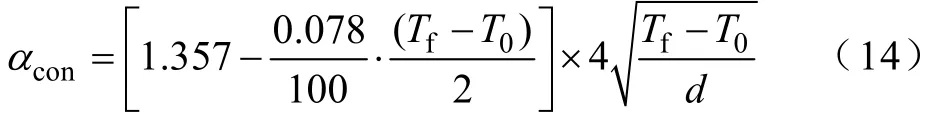
式中d——连接导线直径，对于截面为方形的导线按面积折合成圆形，求得直径d。

热分析时辐射散热系数可通过表面散热系数简化[2]

因此表面总的散热系数为

因此裸导线的散热系数也可由式（16）得到。

外接引线散失的热流量为

式中Awire——外接引线的散热面积；

Twire0——外接引线温度。

外接引线通过载荷电流产生的热功率为

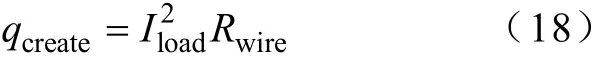
式中Iload——负载电流；

Rwire——外接引线的电阻。

则折合到引线与引出脚连接处的热通量，即热流密度为

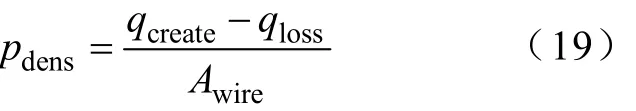
式中Awire——引线的截面积，此处按测试标准取2.5mm2。

此处的热流密度作为载荷加载到触头引出脚的端面上。这样可在建立的模型中去掉外接引线得到简化模型。

4 分析结果温度云图

线圈电压为12V，接触电阻约为2.3mΩ时，加载20A电流，对带外壳及不带外壳两种情况下的继电器温度分布情况各取了几个部分的分析云图。

4.1 带外壳情况下的继电器温度云图

激励电压为12V，加载荷电流20A，带外壳时的温度云图如图2所示。

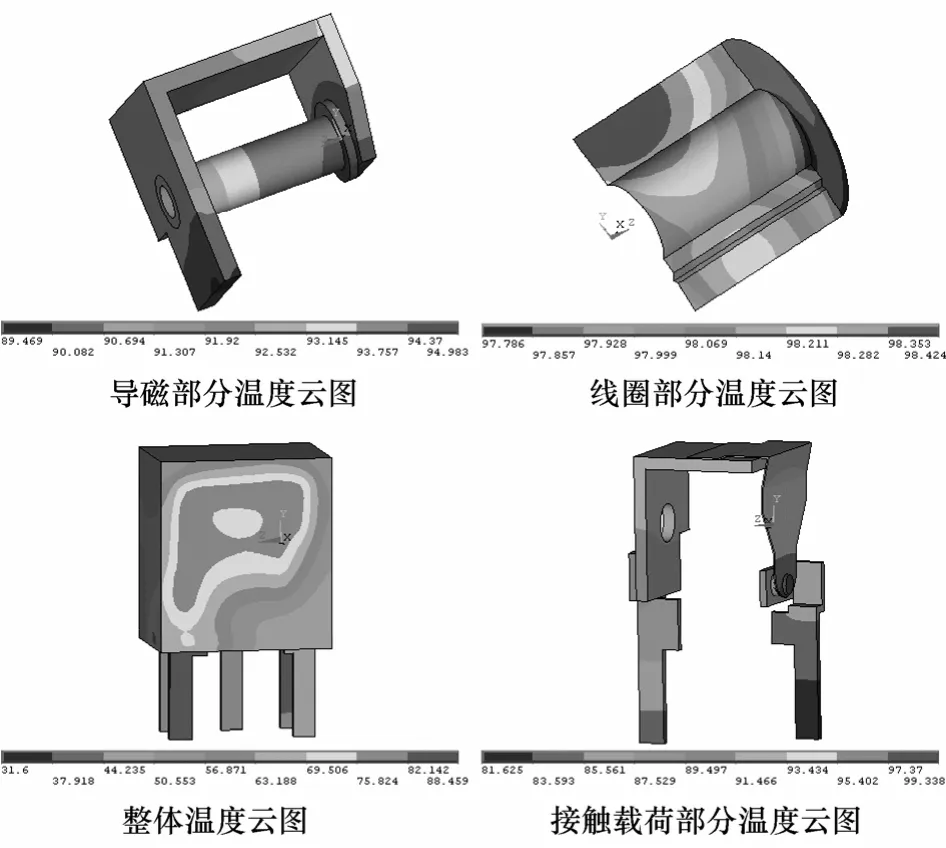
图2 激励电压为12V，加负载20A时的温度云图Fig.2 The temperature contours of model as coil voltage 12V, load current 20A

4.2 不带外壳情况下的继电器温度云图

激励电压为 14.4V，加载荷电流 20A，不带外壳时的温度云图如图3所示。

图3 激励电压为14.4V，加负载20A时去掉外壳的温度云图Fig.3 The temperature contours of model without shell as coil voltage 14.4V, load current 20A

5 结果数据分析

对不同激励电压下均进行了热分析，得到了线圈的温升值，并对计算值与测试值进行了分析和比较。

5.1 带外壳情况下线圈平均温升的分析和比较

不同线圈电压下，加载荷电流20A，对带外壳情况下继电器线圈的平均温升进行了分析，并与实测结果进行了比较。此时试验测试的线圈电压变化范围为7.2～20.4V。

表1为线圈平均温升数据，其中测试温升为试验测试值，计算温升是简化模型后的仿真结果，表中最后一列为含外接引线模型的仿真数据。可以看出简化模型后的计算结果与简化前的计算结果相近，也就是说这种简化是合理的。简化模型的引入也使分析计算得到了简化，是可取的。所以可直接用简化模型仿真实际模型进行计算，试验测试结果和简化模型的计算结果如图4所示。

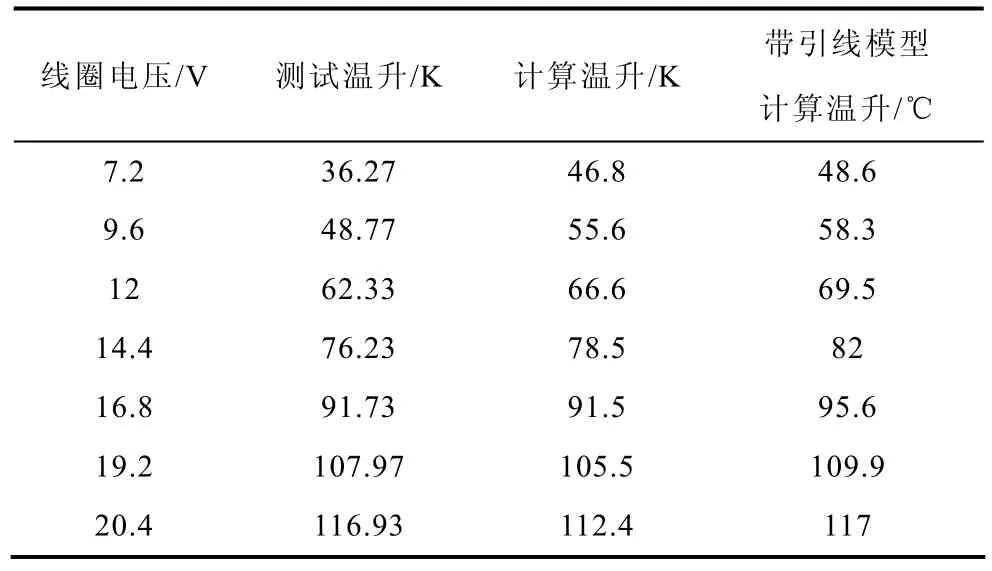
表1 带外壳情况下线圈平均温升Tab.1 Coil average temperature rise with shell

图4 带外壳情况下线圈温升实测值与计算值比较图Fig.4 The coil temperature rise comparison of test and calculation as model with shell

5.2 不带外壳情况下线圈平均温升的分析和比较

此种情况实测值的线圈电压的范围是 14.4～20.4V，所以计算值对应的电压范围也为 14.4～20.4V，且比较的是线圈平均温升实测值和简化模型计算值。分析数据和比较图见表2及图5所示。

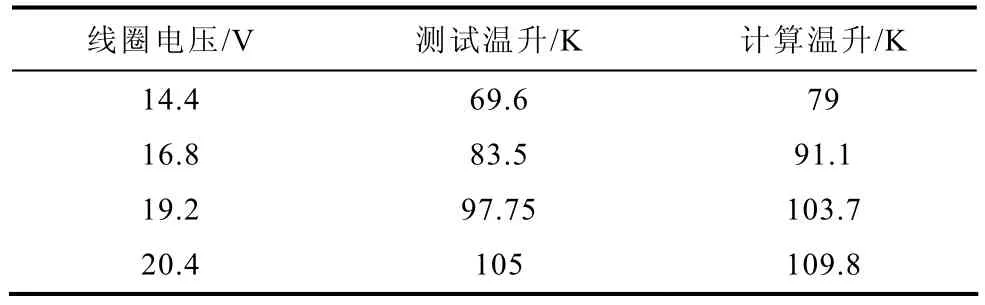
表2 不带外壳情况下线圈平均温升Tab.2 The coil average temperature rise without shell

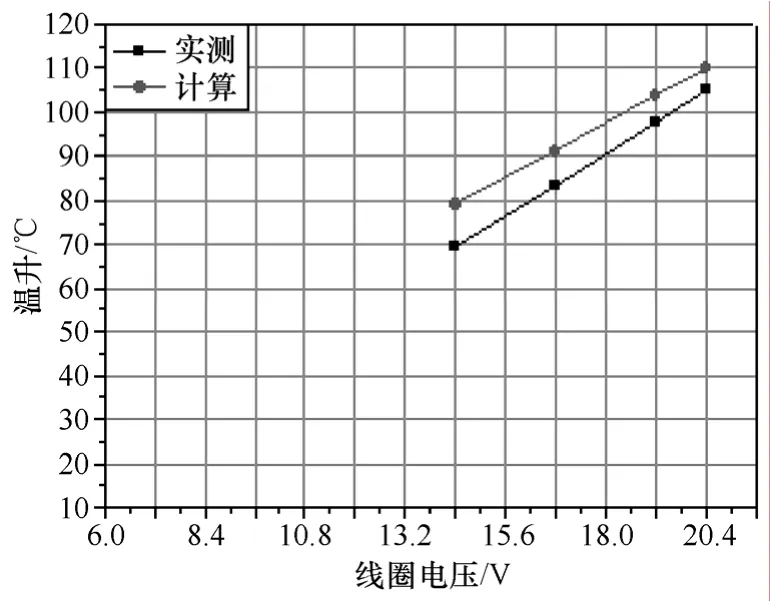
图5 不带外壳情况下线圈温升实测值与计算值比较图Fig.5 The coil temperature rise comparison of test and calculation as model without shell

5.3 结果误差分析

很多材料的热传导率是随温度变化的。本文在做分析时，考虑了一些材料的热传导率变化，计算表明当参数变化率较小时，对结果的影响不大。

本文的对流系数是从经验公式推导出来的，与实际情况存在一定偏差，所以说对流系数是误差的一个来源。另外模型的简化处理也是误差的一个来源，因为在作分析时，简化了一些对结果影响不大的结构特点。此外，一些材料的属性参数不是很准确，这也是误差的一个来源。以上的一些工作需要做进一步研究。

6 结论

本文应用仿真分析软件 ANSYS对某种小型直流电磁继电器的热性能进行了分析。根据电接触理论触头接触处采用等效小圆柱的方法解决了热电耦合分析中接触电阻的发热问题；给出的线圈平均温升计算公式很好地解决了有限元分析时线圈平均温升的计算问题；对带有外接引线的仿真模型与进行当量折合后的简化模型同时做了分析，并对仿真结果进行了比较，结果表明当量折合后的简化模型是可行的。本文对线圈平均温升的仿真结果与实验数据进行了比较，吻合较好。

[1] 黄琳敏, 陈德桂, 张敬菽, 等. 应用瞬态热路法计算直流电磁铁的温升[J]. 低压电器, 2003 (2): 12-15.

Huang Linmin, Chen Degui, Zhang Jingshu, et al.Application of transient thermal circuit in calculating temperature rise of DC electromagnet[J]. Low Voltage Apparatus, 2003 (2): 12-15.

[2] 纽春萍, 陈德桂, 刘颖异, 等. 交流接触器温度场仿真及影响因素的分析[J]. 电工技术学报. 2007,22(5): 71-77.

Niu Chunping, Chen Degui, Liu Yingyi, et al.Temperature field simulation of AC contactor and analysis of its influence factors[J]. Transactions of China Electrotechnical Society, 2007, 22(5): 71-77.

[3] Liang Huimin, Wang Wenlong, Zhai Guofu. Thermal analysis of sealed electromagnetic relays using 3-D finite element method[C]. Proceedings of the 53rd IEEE Holm Conference on Electrical Contacts, 2007:262-268.

[4] Frei Peter U, Weichert Hans O. Advanced thermal simulation of a circuit breaker[C]. Proceedings of the 50th IEEE Holm Conference on Electrical Contacts and the 22nd International Conference on Electrical Contacts, 2004: 104-110.

[5] 程礼春. 电接触理论及应用[M]. 北京: 机械工业出版社, 1988.

[6] 张冠生. 电器理论基础[M]. 北京: 机械工业出版社,1989.

[7] 戴锅生. 传热学[M]. 2版. 北京: 高等教育出版社,1999.

[8] Barcikowski F, Lindamayer M. Simulations of the heat balance in low-voltage switchgear[C].Proceedings of 20th International Conference on Electrical Contacts, Sweden, 2000: 323-329.

[9] 周茂祥. 低压电器设计手册[M]. 北京: 机械工业出版社, 1992.

[10] 方鸿发. 低压电器[M]. 北京: 机械工业出版社,1993.